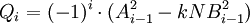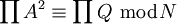- CFRAC
-
Die Kettenbruchmethode (Abk.: CFRAC) berechnet zwei Teiler einer natürlichen Zahl, die keine Primzahl ist. Durch wiederholte Anwendung lässt sich so die Primfaktorzerlegung dieser Zahl ermitteln.
Die Kettenbruchmethode wurde 1931 von Derrick Henry Lehmer und R. E. Powers veröffentlicht. Über Jahrzehnte hinweg wurde sie kaum verwendet, da sie auf den zur Verfügung stehenden Rechenmaschinen häufig nach mehreren Stunden noch keine Faktorisierung fand. Im Jahr 1970 programmierten Michael A. Morrison und John Brillhart die Kettenbruchmethode auf einem Großrechner und berechneten damit die Faktorisierung der siebten Fermat-Zahl. In den achtziger Jahren des zwanzigsten Jahrhunderts war die Kettenbruchmethode das Standardverfahren für die Faktorisierung großer Zahlen. Das waren damals Zahlen mit bis zu fünfzig Dezimalstellen. 1990 wurde mit dem quadratischen Sieb ein neuer Algorithmus vorgestellt, der die Nachfolge der Kettenbruchmethode antrat. Die Laufzeit der Kettenbruchmethode in O-Notation ist
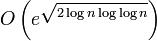 .
.Inhaltsverzeichnis
Algorithmus nach Morrison und Brillhart
Die hier beschriebene Variante der Kettenbruchmethode entspricht derjenigen, die von Morrison und Brillhart in ihrem Aufsatz „A Method of Factoring and the Factorization of F7“ veröffentlicht wurde. Der Algorithmus besteht aus drei wesentlichen Schritten. Die zu faktorisierende Zahl wird im Weiteren mit N bezeichnet.
Schritt A
Wähle eine natürliche Zahl k und berechne die Kettenbruchentwicklung von
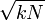 . Die Kettenbruchentwicklung kann an einer beliebigen Stelle n − 1 abgebrochen werden, sodass man einen Kettenbruch der Form
. Die Kettenbruchentwicklung kann an einer beliebigen Stelle n − 1 abgebrochen werden, sodass man einen Kettenbruch der Formerhält. Man berechnet nun die Paare (Ai − 1,Qi), wobei Ai − 1 der Zähler der (i − 1)-ten Konvergente ist und sich Qi nach der Formel
berechnet.
Schritt B
Aus den in Schritt A erzeugten (A,Q)-Paaren werden diejenigen ausgewählt, bei denen alle Primfaktoren von Q einer vorher festgelegten Faktorbasis entstammen. Die Faktorbasis ist üblicherweise eine Menge, die die -1 und alle Primzahlen bis zu einer bestimmten Schranke enthält. Ein Beispiel ist die Menge
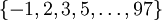 . Durch mehrfache Probedivision lässt sich feststellen, ob das jeweilige Q ein Produkt von Zahlen aus der Faktorbasis ist und nebenbei erhält man die vollständige Primfaktorzerlegung von Q.
. Durch mehrfache Probedivision lässt sich feststellen, ob das jeweilige Q ein Produkt von Zahlen aus der Faktorbasis ist und nebenbei erhält man die vollständige Primfaktorzerlegung von Q.Mit den ausgewählten (A,Q)-Paaren füllt man eine Tabelle. Diese Tabelle enthält eine Spalte für jede Zahl der Faktorbasis. In die Faktorbasisspalten wird eine Eins eingetragen, wenn der jeweilige Faktor in der Primzahlzerlegung von Q ungerade oft vorkommt. Andernfalls trägt man eine Null ein. Der Tabelleneintrag für das Paar
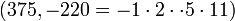 und die Faktorbasis { − 1,2,3,5,7,11,13} sieht beispielsweise wie folgt aus.
und die Faktorbasis { − 1,2,3,5,7,11,13} sieht beispielsweise wie folgt aus.-1 2 3 5 7 11 13 (375, -220) 1 0 0 1 0 1 0 Schritt C
Für jede der Teilmengen multipliziert man die As aller Paare und die Qs aller Paare. So erhält man die Legendre-Kongruenz
Berechne die Teiler
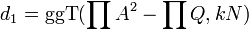 und
und 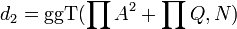 von N.
von N.Geschichte
Der erste Schritt auf dem Weg zur Kettenbruchmethode war die 1643 von Pierre de Fermat beschriebene Faktorisierungsmethode von Fermat. Dieses Rechenverfahren findet zwei Quadratzahlen x2 und y2, sodass x2 − y2 = N gilt. N ist auch hier wieder die zu faktorisierende Zahl. Aufgrund der 3. Binomischen Formel gilt
- N = x2 − y2 = (x + y)(x − y)
und x + y und x − y sind deshalb Teiler von N.
1798 veröffentlichte Adrien-Marie Legendre sein Buch „Essai sur la théorie des nombres“. In diesem findet sich mit den Legendre-Kongruenzen eine Weiterentwicklung der Methode von Fermat. Die Differenz der Quadratzahlen x2 und y2 muss nicht mehr gleich N sein, sondern kann ein beliebiges Vielfaches von N sein. Die Wurzeln x und y der Quadratzahlen müssen zudem drei Bedingungen erfüllen: 0 < x,y < N,
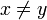 und
und 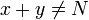 . Unter diesen Voraussetzung ist N ein Teiler von x2 − y2 = (x + y)(x − y) und sowohl der größte gemeinsame Teiler
. Unter diesen Voraussetzung ist N ein Teiler von x2 − y2 = (x + y)(x − y) und sowohl der größte gemeinsame Teiler 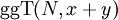 als auch
als auch 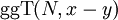 sind Faktoren von N.
sind Faktoren von N.Literatur
- Carl Pomerance: A Tale of Two Sieves. In: Notices of the AMS. Bd. 43, Nr. 12, 1996, S. 1473–1485
- Derrick Henry Lehmer, R. E. Powers: On Factoring Large Numbers. In: Bulletin of the American Mathematical Society. Bd. 37, 1931, S. 770–776 (doi:10.1090/S0002-9904-1931-05271-X)
- Michael A. Morrison, John Brillhart: A Method of Factoring and the Factorization of F7. In: Mathematics of Computation. Bd. 29, Nr. 129, 1975, S. 183–205 (doi:10.2307/2005475)
Wikimedia Foundation.

![[ q_0; q_1, q_2, \ldots, q_{n-1}, \frac{\sqrt{kN} + P_n}{Q_n}]](/pictures/dewiki/53/5435669fef4fba25b977cda546e426fc.png)