- Cauchy-Netz
-
Ein Netz oder eine Moore-Smith-Folge stellt in der Topologie (einem Teilgebiet der Mathematik) eine Verallgemeinerung einer Folge dar. Der Begriff geht auf Eliakim Hastings Moore und H. L. Smith zurück. Mit Cauchynetzen lässt sich der Begriff der Vollständigkeit von Metrischen Räumen auf uniforme Räume verallgemeinern. Darüber hinaus kann man sie in der Integralrechnung zur Beschreibung der Riemann-Integrierbarkeit verwenden.
Inhaltsverzeichnis
Definitionen
Für eine gerichtete Menge
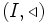 und eine Menge X ist ein Netz eine Abbildung
und eine Menge X ist ein Netz eine Abbildung 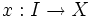 . Meist schreibt man analog zu Folgen
. Meist schreibt man analog zu Folgen 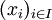 . Da die natürlichen Zahlen mit der gewöhnlichen Anordnung eine gerichtete Menge bilden, sind Folgen spezielle Netze.
. Da die natürlichen Zahlen mit der gewöhnlichen Anordnung eine gerichtete Menge bilden, sind Folgen spezielle Netze.Teilnetz
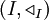 und
und 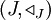 seien gerichtete Mengen,
seien gerichtete Mengen, 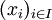 ein Netz in X und
ein Netz in X und 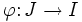 eine Abbildung, die der folgenden Bedingung genügt:
eine Abbildung, die der folgenden Bedingung genügt:(Eine solche Abbildung φ heißt kofinal). Dann nennt man das Netz
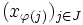 ein Teilnetz des Netzes
ein Teilnetz des Netzes 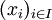 .
.Konvergentes Netz
Ist X ein topologischer Raum, so definiert man wie bei Folgen: Ein Netz heißt konvergent gegen
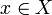 , wenn gilt:
, wenn gilt:Man schreibt dann
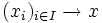 oder
oder 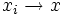 . Die formale Definition lässt sich so umschreiben: Für jede Umgebung von x gibt es einen Anfangsindex i0 in der gerichteten Menge I, so dass Glieder des Netzes mit Index i nach
. Die formale Definition lässt sich so umschreiben: Für jede Umgebung von x gibt es einen Anfangsindex i0 in der gerichteten Menge I, so dass Glieder des Netzes mit Index i nach 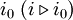 in der vorgelegten Umgebung enthalten sind.
in der vorgelegten Umgebung enthalten sind.Cauchynetz
Ist (X,Φ) ein uniformer Raum, so definiert man: Ein Netz auf X heißt Cauchynetz, wenn zu jeder Nachbarschaft
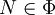 ein Index
ein Index 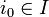 existiert, so dass alle Paare von Gliedern des Netzes mit späteren Indizes
existiert, so dass alle Paare von Gliedern des Netzes mit späteren Indizes 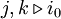 von der Ordnung N benachbart sind, d. h. dass
von der Ordnung N benachbart sind, d. h. dass 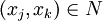 gilt. Die formalisierte Definition lautet
gilt. Die formalisierte Definition lautetVollständigkeit
Ein uniformer Raum X ist genau dann vollständig, wenn jedes Cauchynetz auf X konvergent ist.
Anwendungen
- Definition der abgeschlossenen Hülle
Ist A eine Teilmenge des topologischen Raumes X, dann ist
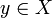 genau dann ein Berührpunkt von A (d. h. in der abgeschlossenen Hülle von A enthalten), wenn es ein Netz
genau dann ein Berührpunkt von A (d. h. in der abgeschlossenen Hülle von A enthalten), wenn es ein Netz 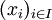 mit Gliedern
mit Gliedern 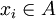 gibt, das gegen y konvergiert.
gibt, das gegen y konvergiert.- Lokale Definition der Stetigkeit
- Seien X und Y topologische Räume. Eine Abbildung
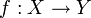 ist stetig im Punkt
ist stetig im Punkt 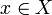 genau dann, wenn für jedes Netz
genau dann, wenn für jedes Netz 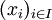 in X gilt: Aus
in X gilt: Aus 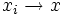 folgt
folgt 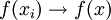 .
.
- Riemann-Integral
Die Menge
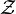 der Zerlegungen
der Zerlegungen 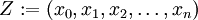 des reellen Intervalls [a,b],
des reellen Intervalls [a,b], 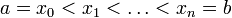 , wird durch die Inklusion zu einer gerichteten Menge:
, wird durch die Inklusion zu einer gerichteten Menge: 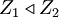 : Z2 enthält alle Punkte von Z1. Für eine reellwertige beschränkte Funktion auf [a,b] werden durch die Obersumme
: Z2 enthält alle Punkte von Z1. Für eine reellwertige beschränkte Funktion auf [a,b] werden durch die Obersummeund die Untersumme
zwei Netze definiert. Die Funktion f ist genau dann Riemann-integrierbar auf [a,b], wenn beide Netze gegen die gleiche reelle Zahl c konvergieren. In dem Fall ist
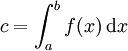 .
.Literatur
- Boto v. Querenburg: Mengentheoretische Topologie. 3. Auflage. Springer, Berlin 2001, ISBN 3540677909
- E. H. Moore, H. L. Smith (1922): A General Theory of Limits. American Journal of Mathematics 44 (2), 102–121
- Lydia Außenhofer: Mengentheoretische Topologie.
Wikimedia Foundation.

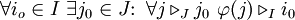
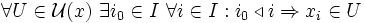
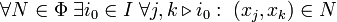
![\mathbf{O}(f) : \mathcal{Z} \to \Bbb{R}; (x_0,x_1,x_2,\ldots, x_n) \mapsto \sum_{j=1}^n (x_j-x_{j-1})\cdot\sup_{x\in [x_{j-1},x_j]} f(x)](/pictures/dewiki/51/32cd9d5ce60514af66a94700f07661db.png)
![\mathbf{U}(f) : \mathcal{Z} \to \Bbb{R}; (x_0,x_1,x_2,\ldots, x_n) \mapsto \sum_{j=1}^n (x_j-x_{j-1})\cdot\inf_{x\in [x_{j-1},x_j]} f(x)](/pictures/dewiki/98/bb924693e3805f590ff4223bd74034b4.png)