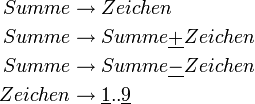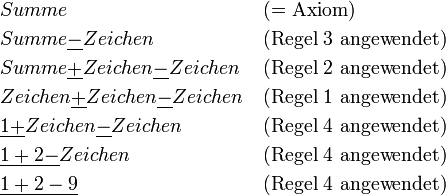- Chomsky-Typ
-
Chomsky-Hierarchie, gelegentlich Chomsky–Schützenberger-Hierarchie, (benannt nach dem Linguisten Noam Chomsky und dem Mathematiker Marcel Schützenberger) ist ein Begriff aus der Theoretischen Informatik und bezeichnet eine Hierarchie von Klassen formaler Grammatiken, die formale Sprachen erzeugen. Sie wurde 1956 erstmals von Noam Chomsky beschrieben. Die vier von Chomsky beschriebenen Grammatiktypen entstehen dabei ausgehend von einer nicht eingeschränkten Grundgrammatik (der Typ-0-Grammatik) indem zunehmend Einschränkungen bezüglich der für den Typ erlaubten Produktionsregeln gemacht werden.
Entsprechend des Typs einer Grammatik, die mindestens erforderlich ist, um eine bestimmte formale Sprache zu erzeugen, werden auch formale Sprachen in dieselben Kategorien von Typ 0 bis Typ 3 eingeteilt.
Inhaltsverzeichnis
Erläuterungen zur Grundidee
In der Informatik spielen sog. formale Sprachen eine wichtige Rolle. Sie erlauben Informationen in einer computerverständlichen Form darzustellen und verarbeiten zu lassen. Eine formale Sprache weist gewisse Parallelen zu natürlichen Sprachen auf. Sie besteht aus einer Menge von sogenannten terminalen Zeichen (in natürlichen Sprachen Silben), die zu Wörtern zusammengefügt werden können. Außerdem gibt es einen Satz von Regeln (Grammatik genannt), der beschreibt, wie aus Wörtern sogenannte gültige Ausdrücke (entsprechend natürlichen Sätzen) aufgebaut werden können. Die hier angemerkten Entsprechungen sind keine absoluten Parallelen, geben aber eine ungefähre Idee des Konzepts. Beispiele für den Einsatz von formalen Sprachen sind etwa Programmiersprachen oder Auszeichnungssprachen wie XML oder HTML. Sie lassen sich alle als formale Sprache ausdrücken. Es sei angemerkt, dass die formale Sprache nur das Konzept der Datendarstellung beschreibt (z. B. die Idee, dass eine XML-Datei aus verschachtelten Tags aufgebaut ist), nicht die tatsächlichen Daten.
Die Idee hinter formalen Sprachen ist es, eine mathematisch exakte Beschreibung für eine solche Sprache zu finden. Darauf aufbauend können dann Verfahren konstruiert werden, die diese Sprachen verarbeiten (sog. Parser). Im letzten Absatz wurden schon die Grundelemente einer formalen Sprache genannt. Zum einen muss es eine Menge von Grundzeichen geben. Sie wird als Alphabet Σ bezeichnet und kann z. B. die Menge aller Buchstaben und aller Ziffern sein. Das zweite Grundelement ist die Grammatik mit ihren Regeln. Grammatiken werden hier durch Ersetzungsregeln
 dargestellt. Damit kann man in einem gültigen Wort der Sprache die Zeichen α durch die Zeichen β ersetzen und erhält wieder ein gültiges Wort. Zusätzlich benötigt man noch ein Startzeichen, oft auch als Axiom bezeichnet. Das ist ein Zeichen, das per Definition ein Wort der Sprache ist. Man muss hier noch zwischen terminalen und nicht-terminalen Symbolen unterscheiden. Streng genommen dürfen Sätze oder Wörter einer formalen Sprache nur aus Terminalsymbolen (z. B. den Buchstaben des Alphabets) bestehen. Es werden aber noch sog. Nicht-Terminale (oder Variablen) eingeführt. Das sind Platzhaltersymbole, die in gewisser Weise ein Konzept repräsentieren. Das folgende Beispiel verdeutlicht das. Es beschreibt eine Sprache, die einfache mathematische Ausdrücke (Summen) erzeugt. Terminalsymbole sind unterstrichen dargestellt, Nicht-Terminale kursiv. Jede Zeile stellt eine Regel dar.
dargestellt. Damit kann man in einem gültigen Wort der Sprache die Zeichen α durch die Zeichen β ersetzen und erhält wieder ein gültiges Wort. Zusätzlich benötigt man noch ein Startzeichen, oft auch als Axiom bezeichnet. Das ist ein Zeichen, das per Definition ein Wort der Sprache ist. Man muss hier noch zwischen terminalen und nicht-terminalen Symbolen unterscheiden. Streng genommen dürfen Sätze oder Wörter einer formalen Sprache nur aus Terminalsymbolen (z. B. den Buchstaben des Alphabets) bestehen. Es werden aber noch sog. Nicht-Terminale (oder Variablen) eingeführt. Das sind Platzhaltersymbole, die in gewisser Weise ein Konzept repräsentieren. Das folgende Beispiel verdeutlicht das. Es beschreibt eine Sprache, die einfache mathematische Ausdrücke (Summen) erzeugt. Terminalsymbole sind unterstrichen dargestellt, Nicht-Terminale kursiv. Jede Zeile stellt eine Regel dar.Das Axiom dieser Sprache ist Summe. Davon ausgehend kann man nun beliebige Regeln nacheinander anwenden, um einen gültigen Ausdruck zu erzeugen:
Die angewendeten Regeln sind willkürlich gewählt. Die Grammatik gibt nur vor, welche Regeln in einer Situation anwendbar sind, nicht welche angewendet werden müssen oder sollen. In der ersten Zeile sind z. B. nur die Regeln 1-3 anwendbar, nicht aber Regel 4. Ab dem 4. Schritt ist nur noch Regel 4 anwendbar.
Es ist nun möglich auch komplexere Grammatiken (und damit komplexere formale Sprachen) zu entwerfen. So ist z. B. die Syntax der Programmiersprache Pascal als formale Grammatik gegeben.[1]
Die Chomsky-Hierarchie versucht nun eine Klassifizierung der im Prinzip unbeschränkten Sprachen, also der Sätze von Symbolen und Regeln. Dabei werden bestimmte Klassen von Sprachen eingeführt, für die sich zeigen lässt, in welcher Geschwindigkeit und auf welche Art und Weise sie von einem Computer verarbeitet werden können. Dabei werden die Sprachen umso eingeschränkter, je tiefer sie in der Hierarchie liegen. Allgemein lässt sich beobachten, dass die einfacheren Sprachen auf der einen Seite auch einfacher (und schneller) zu verarbeiten, aber andererseits auch nicht so mächtig sind. Ein Beispiel: Oft werden sogenannte reguläre Ausdrücke eingesetzt, um mächtige Suchfunktionen in Texten zu realisieren. Reguläre Ausdrücke sind Chomsky-Grammatiken vom Typ 3. Sie sind zwar einfach genug, um große Textmengen mit solchen Ausdrücken zu durchsuchen, sie sind aber nicht mächtig genug, um Programmiersprachen zu beschreiben. Diese sind typischerweise Chomsky-Typ 2 Sprachen.
Im folgenden werden diese anschaulichen Erläuterungen mathematisch streng gefasst und die Aussagen präzisiert.
Übersicht
Zunächst sei im Folgenden die formale Grammatik G = (N,Σ,P,S) angenommen. N stellt die Menge der Nichtterminalsymbole, Σ die Menge der Terminalsymbole, P die Menge von Produktionsregeln und S das Startsymbol dar (Einzelheiten siehe unter formale Grammatik).
Die folgende Tabelle fasst die vier Grammatiktypen, die Form ihrer Regeln, die Sprachen, die sie erzeugen und die Automatentypen, die sie erkennen, zusammen. Zudem wird die Abgeschlossenheit der erzeugten Sprachen bezüglich einiger Operationen angegeben.
Grammatik Regeln Sprachen Automaten Abgeschlossenheit Typ-0 
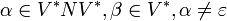
rekursiv aufzählbar Turingmaschine KSV* Typ-1 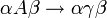
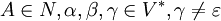
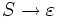 ist erlaubt, wenn es keine Regel
ist erlaubt, wenn es keine Regel 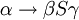 in P gibt.
in P gibt.kontextsensitiv linear platzbeschränkte nichtdeterministische Turingmaschine CKSV* Typ-2 
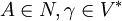
kontextfrei nichtdeterministischer Kellerautomat KV* Typ-3 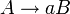 (rechtsregulär) oder
(rechtsregulär) oder
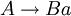 (linksregulär)
(linksregulär)
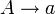
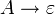
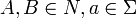
regulär Endlicher Automat CKSV* Mengensymbole
- Σ: Menge der Terminalsymbole
- N: Menge der Nichtterminalsymbole
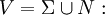 Vokabular der Grammatik (Menge aller Terminal- und Nichtterminalsymbole)
Vokabular der Grammatik (Menge aller Terminal- und Nichtterminalsymbole)
Abgeschlossenheit
- C = Komplementbildung
- K = Konkatenation
- S = Schnittmenge
- V = Vereinigungsmenge
- * = Kleenescher Abschluss
Die Hierarchie
Typ-0-Grammatik (allgemeine Chomsky-Grammatik oder Phrasenstrukturgrammatik)
Typ-0-Grammatiken werden auch unbeschränkte Grammatiken genannt. Es handelt sich dabei um alle definierbaren Grammatiken.
Man schreibt
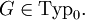
Jede Typ-0-Grammatik erzeugt eine Sprache, die von einer Turingmaschine akzeptiert werden kann und umgekehrt existiert für jede Sprache, die von einer Turingmaschine akzeptiert werden kann, eine Typ-0-Grammatik, die diese Sprache erzeugt. Diese Sprachen sind auch bekannt als die rekursiv aufzählbaren Sprachen (oft auch semi-entscheidbare Sprachen genannt), d. h. die zugehörige Turingmaschine hält bei jedem Wort, das in der Sprache liegt, und liefert das Ergebnis 1. Es ist allerdings nicht gefordert, dass die Turingmaschine für ein Wort, das nicht in der Sprache liegt, mit dem Ergebnis 0 hält (die Maschine muss also nicht terminieren).
Man beachte, dass sich diese Menge von Sprachen von der Menge der rekursiven Sprachen (oft auch entscheidbare Sprachen genannt) unterscheidet, welche durch Turingmaschinen entschieden werden können.
Typ-1-Grammatik (kontextsensitive bzw. monotone Grammatik)
Typ-1-Grammatiken werden auch kontextsensitive Grammatiken genannt. Es handelt sich dabei um Typ-0-Grammatiken bei denen für alle Produktionsregeln
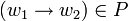 gilt:
gilt: 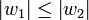 , also die rechte Seite der Regel (w2) nicht weniger Elemente enthält als die linke Seite der Regel (w1) - die Regeln dürfen also nicht verkürzend sein.
, also die rechte Seite der Regel (w2) nicht weniger Elemente enthält als die linke Seite der Regel (w1) - die Regeln dürfen also nicht verkürzend sein.Man schreibt
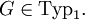
Sie erzeugen genau die kontextsensitiven Sprachen, das heißt jede Typ-1-Grammatik erzeugt eine kontextsensitive Sprache und zu jeder kontextsensitiven Sprache existiert eine Typ-1-Grammatik, die diese erzeugt.
Typ-1-Grammatiken besitzen nur Regeln der Form
 wobei A ein Nichtterminal und α,γ,β Wörter bestehend aus Terminalen (Σ) und Nichtterminalen (N) sind. Die Wörter α und β können leer sein, aber γ muss mindestens ein Symbol (also ein Terminal oder ein Nichtterminal) enthalten. Diese Eigenschaft wird Längenbeschränktheit genannt.
wobei A ein Nichtterminal und α,γ,β Wörter bestehend aus Terminalen (Σ) und Nichtterminalen (N) sind. Die Wörter α und β können leer sein, aber γ muss mindestens ein Symbol (also ein Terminal oder ein Nichtterminal) enthalten. Diese Eigenschaft wird Längenbeschränktheit genannt.Die einzige Ausnahme ist, dass die Grammatik die Regel
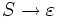 ausgehend vom Startsymbol S enthalten darf. Diese Regel wird eventuell benötigt, um das leere Wort
ausgehend vom Startsymbol S enthalten darf. Diese Regel wird eventuell benötigt, um das leere Wort  ableiten zu können. Die Regel
ableiten zu können. Die Regel 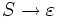 darf aber nur dann verwendet werden, wenn das Startsymbol S auf keiner rechten Seite der Produktionsregeln auftritt.
darf aber nur dann verwendet werden, wenn das Startsymbol S auf keiner rechten Seite der Produktionsregeln auftritt.Die kontextsensitiven Sprachen sind genau die Sprachen, die von einer nichtdeterministischen, linear beschränkten Turingmaschine erkannt werden können; das heißt von einer nichtdeterministischen Turingmaschine, deren Band linear durch die Länge der Eingabe beschränkt ist (das heißt es gibt eine konstante Zahl a so dass das Band der Turingmaschine höchstens
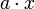 Felder besitzt, wobei x die Länge des Eingabewortes ist).
Felder besitzt, wobei x die Länge des Eingabewortes ist).Im Unterschied zu kontextfreien Grammatiken kann die Anzahl der Symbole auf der linken Seite einer kontextsensitiven Grammatik > 1 sein.
Typ-2-Grammatik (kontextfreie Grammatik)
Typ-2-Grammatiken werden auch kontextfreie Grammatiken genannt. Es handelt sich dabei um Typ-1-Grammatiken mit
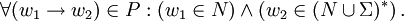 Für jede Regel der Grammatik gilt also, dass auf der linken Seite der Regel genau ein nicht-terminales Symbol steht, und auf der rechten Seite eine beliebige (auch leere) Folge von terminalen und nicht-terminalen Symbolen. Jede Regel einer Typ-2-Grammatik stellt somit eine Definition für ein nicht-terminales Symbol dieser Grammatik dar.
Für jede Regel der Grammatik gilt also, dass auf der linken Seite der Regel genau ein nicht-terminales Symbol steht, und auf der rechten Seite eine beliebige (auch leere) Folge von terminalen und nicht-terminalen Symbolen. Jede Regel einer Typ-2-Grammatik stellt somit eine Definition für ein nicht-terminales Symbol dieser Grammatik dar.Man schreibt
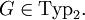
Sie erzeugen genau die kontextfreien Sprachen, d. h. jede Typ-2-Grammatik erzeugt eine kontextfreie Sprache und zu jeder kontextfreien Sprache existiert eine Typ-2-Grammatik, die diese erzeugt.
Typ-2-Grammatiken besitzen nur Regeln der Form
 wobei A ein Nichtterminal und γ ein Wort bestehend aus Terminalen und Nichtterminalen ist. (Um das leere Wort
wobei A ein Nichtterminal und γ ein Wort bestehend aus Terminalen und Nichtterminalen ist. (Um das leere Wort  zu erzeugen, darf hier für γ auch
zu erzeugen, darf hier für γ auch  verwendet werden.)
verwendet werden.)Die kontextfreien Sprachen sind genau die Sprachen, die von einem nichtdeterministischen Kellerautomaten (NPDA) erkannt werden können. Eine Teilmenge dieser Sprachen bildet die theoretische Basis für die Syntax der meisten Programmiersprachen.
Siehe auch hier: Backus-Naur-Form.
Typ-3-Grammatik (rechtslineare bzw. linkslineare Grammatik)
Typ-3-Grammatiken werden auch reguläre Grammatiken genannt. Es handelt sich dabei um Typ-2-Grammatiken mit
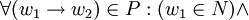
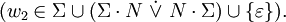 Auf der linken Seite jeder Regel der Grammatik steht also genau ein nicht-terminales Symbol. Auf der rechten Seite steht bei den sogenannten rechtsregulären Grammatiken genau ein Terminal, optional gefolgt von einem Nicht-Terminal. Bei den sogenannten linksregulären Grammatiken steht auf der rechten Seite jeder Regel ein Terminal, dem optional ein Nicht-Terminal vorangeht.
Auf der linken Seite jeder Regel der Grammatik steht also genau ein nicht-terminales Symbol. Auf der rechten Seite steht bei den sogenannten rechtsregulären Grammatiken genau ein Terminal, optional gefolgt von einem Nicht-Terminal. Bei den sogenannten linksregulären Grammatiken steht auf der rechten Seite jeder Regel ein Terminal, dem optional ein Nicht-Terminal vorangeht.Man schreibt
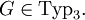
Sie erzeugen genau die regulären Sprachen, das heißt, jede Typ-3-Grammatik erzeugt eine reguläre Sprache und zu jeder regulären Sprache existiert eine Typ-3-Grammatik, die diese erzeugt.
Typ-3-Grammatiken besitzen entweder nur Regeln, die auf der linken Seite aus einem Nichtterminal und auf der rechten Seite aus einem Terminal, eventuell gefolgt von einem Nichtterminal bestehen (rechtslineare Grammatik) oder nur Regeln, die auf der linken Seite aus einem Nichtterminal und auf der rechten Seite aus einem Terminal, eventuell mit vorangestelltem Nichtterminal bestehen (linkslineare Grammatik).
Zu jeder linkslinearen Grammatik gibt es auch eine rechtslineare Grammatik, und umgekehrt, welche dieselbe Sprache erzeugt.
Reguläre Sprachen können alternativ auch durch reguläre Ausdrücke beschrieben werden und die regulären Sprachen sind genau die Sprachen, die von endlichen Automaten erkannt werden können. Sie werden häufig genutzt, um Suchmuster oder die lexikalische Struktur von Programmiersprachen zu definieren.
Chomsky-Hierarchie für formale Sprachen
Eine formale Sprache L ist vom Typ
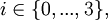 falls es eine Grammatik
falls es eine Grammatik 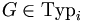 mit
mit 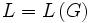 gibt. Man schreibt dann
gibt. Man schreibt dann 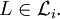
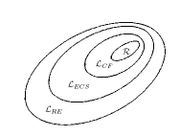
Jede reguläre Sprache ist kontextfrei, jede kontextfreie Sprache ist kontextsensitiv und jede kontextsensitive Sprache ist rekursiv aufzählbar. Dabei handelt es sich um echte Teilmengenbeziehungen, das heißt es gibt rekursiv aufzählbare Sprachen, die nicht kontextsensitiv sind, kontextsensitive Sprachen, die nicht kontextfrei sind und kontextfreie Sprachen, die nicht regulär sind.
Formal ausgedrückt bedeutet dies für die Klassen der durch die obigen Grammatiken erzeugten Sprachen:
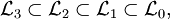 wobei gelegentlich auch folgende Symbole verwendet werden:
wobei gelegentlich auch folgende Symbole verwendet werden: 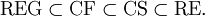
Beispiele für Sprachen in den jeweiligen Differenzmengen sind:
- Das Halteproblem ist vom Typ 0, aber nicht vom Typ 1
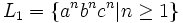 ist vom Typ 1, aber nicht vom Typ 2
ist vom Typ 1, aber nicht vom Typ 2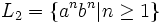 ist vom Typ 2, aber nicht vom Typ 3
ist vom Typ 2, aber nicht vom Typ 3
Natürliche Sprachen
Obwohl Chomsky seine Forschungen mit dem Ziel verfolgte, eine mathematische Beschreibung der natürlichen Sprachen zu finden, ist bis heute der Nachweis einer (formalen) Grammatik nur für die wenigsten Sprachen gelungen, die meisten davon konstruierte Plansprachen. Das Problem besteht vor allem in der Mehrdeutigkeit menschlicher Kommunikation mit ihren verschiedenen Bedeutungsebenen. So kann sich in dem Satz „Ich sehe den Mann auf dem Hügel mit dem Fernrohr.“ das Fernrohr sowohl auf dem Hügel, als auch in der Hand des Sprechers befinden. Damit sind für diesen Satz zwei unterschiedliche Grammatikregeln möglich. Die korrekte Bedeutung ergibt sich aus dem erweiterten Kontext, in dem dieser Satz steht, oder kann sogar unaufgelöst bleiben. Selbst um die Mehrdeutigkeit überhaupt erst erkennen zu können, benötigt man einen kulturellen Hintergrund, der ebenfalls schwer mathematisch darstellbar ist. Die heutigen Übersetzungssysteme umgehen diese Formalisierung und nutzen Datenbanken mit Redewendungen, die den jeweiligen Kontext mitliefern. Die Übersetzung bleibt mechanisch. Die Bedeutung muss der Leser selbst dem Text entlocken. Wenn in einem übersetzten Text nur die Vokabeln stimmen, hat der menschliche Leser in der Regel keine Schwierigkeiten bei der inhaltlichen Erfassung; somit ist eine praktikable automatische Übersetzung ganz ohne Expertensystem möglich geworden.
Literatur
- Noam Chomsky: Three models for the description of language (pdf). In: IRE Transactions on Information Theory 2 (1956), S. 113–124
- Noam Chomsky: On certain formal properties of grammars. In: Information and Control 2 (1959), S. 137-167
- Noam Chomsky, Marcel P. Schützenberger: The algebraic theory of context free languages, Computer Programming and Formal Languages (P. Braffort and D. Hirschberg ed.), North Holland, Amsterdam, 1963, 118-161.
- Sander, Stucky, Herschel: Automaten, Sprachen, Berechenbarkeit. B. G. Teubner, Stuttgart 1992, ISBN 3-519-02937-5
Einzelnachweise
Wikimedia Foundation.