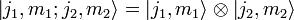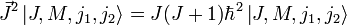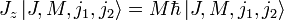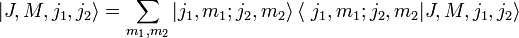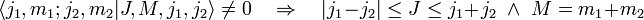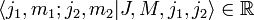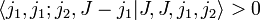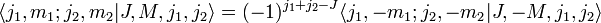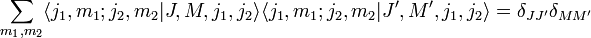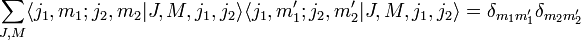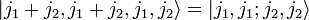- Clebsch-Gordon-Koeffizienten
-
Die Clebsch-Gordan-Koeffizienten finden ihre Verwendung in der Kopplung quantenmechanischer Drehimpulse. Es handelt sich dabei um Entwicklungskoeffizienten, mit denen man aus der Basis der Einzeldrehimpulse in die Basis des Gesamtdrehimpulses übergeht. Sie werden zur Berechnung der Spin-Bahn-Kopplung sowie im Isospin-Formalismus verwendet.
Sie wurden nach Alfred Clebsch (1833-1872) und Paul Albert Gordan (1837-1912) benannt.
Inhaltsverzeichnis
Drehimpulskopplung
Siehe auch den Abschnitt "Addition von Drehimpulsen" im Artikel Drehimpulsoperator.
Man geht von zwei Drehimpulsen J1 und J2 aus, die jeweils die Quantenzahlen j1 und m1 (z-Komponente), bzw. j2 und m2 besitzen. Dabei nehmen m1 und m2 folgende Werte an: m1 = [ − j1,...,j1] und m2 = [ − j2,...,j2] und die Drehimpulse vertauschen untereinander: [J1,J2] = 0 (s. Quantenmechanischer Kommutator). Das bedeutet, dass man die einzelnen Drehimpulse unabhängig von einander scharf messen kann. Jeder dieser Drehimpulse hat seinen eigenen Eigenraum, der durch die Eigenvektoren
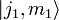 bzw.
bzw. 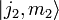 aufgespannt wird. In der Basis dieser Eigenvektoren
aufgespannt wird. In der Basis dieser Eigenvektoren 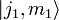 hat J1 eine einfache diagonale Gestalt; analoges gilt für J2.
hat J1 eine einfache diagonale Gestalt; analoges gilt für J2.Nun koppeln die einzelnen Drehimpulse J1 und J2 zu einem Gesamtdrehimpuls
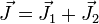 (Addition der einzelnen Komponenten). Dieser Gesamtdrehimpuls besitzt nun die Quantenzahlen J und M, die folgende Werte annehmen können:
(Addition der einzelnen Komponenten). Dieser Gesamtdrehimpuls besitzt nun die Quantenzahlen J und M, die folgende Werte annehmen können: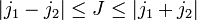 und M = [ − J,...,J] (in ganzzahligen Schritten).
und M = [ − J,...,J] (in ganzzahligen Schritten).
Da der Gesamtdrehimpuls
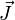 aus beiden Drehimpulsen J1 und J2 besteht, kann er im Produktraum der einzelnen Eigenzustände dargestellt werden.
aus beiden Drehimpulsen J1 und J2 besteht, kann er im Produktraum der einzelnen Eigenzustände dargestellt werden.Allerdings sind dies keine Eigenvektoren des Gesamtdrehimpulses
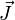 , so dass er in dieser Basis keine Diagonalgestalt besitzt.
, so dass er in dieser Basis keine Diagonalgestalt besitzt.Eigenbasis des Gesamtdrehimpulsoperators
Die Eigenvektoren von
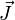 werden durch die Quantenzahlen J, M, j1 und j2 eindeutig festgelegt. Bezüglich der neuen Basis aus Eigenvektoren hat der Gesamtdrehimpuls J wieder eine einfache Diagonalgestalt. Es gilt:
werden durch die Quantenzahlen J, M, j1 und j2 eindeutig festgelegt. Bezüglich der neuen Basis aus Eigenvektoren hat der Gesamtdrehimpuls J wieder eine einfache Diagonalgestalt. Es gilt:Die Clebsch-Gordan-Koeffizienten geben nun den Übergang der Produktbasis
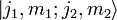 in die Eigenbasis
in die Eigenbasis 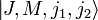 an (unitäre Transformation).
an (unitäre Transformation).Dabei sind
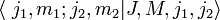 die Clebsch-Gordan-Koeffizienten.
die Clebsch-Gordan-Koeffizienten.Eigenschaften der Clebsch-Gordan-Koeffizienten
- Die Clebsch-Gordan-Koeffizienten sind gleich Null, wenn eine der beiden Bedingungen
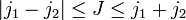 und M = m1 + m2 nicht erfüllt ist:
und M = m1 + m2 nicht erfüllt ist:
- Die Clebsch-Gordan-Koeffizienten sind konventionsgemäß reell:
- Folgender Clebsch-Gordan-Koeffizient zu M = J ist konventionsgemäß positiv:
- Der Clebsch-Gordan-Koeffizient zu M ist betragsmäßig gleich dem Clebsch-Gordan-Koeffizient zu − M gemäß:
- Die Clebsch-Gordan-Koeffizienten erfüllen die Orthogonalitätsrelation:
- Die Clebsch-Gordan-Koeffizienten erfüllen die Orthogonalitätsrelation:
Ermittlung der Clebsch-Gordan-Koeffizienten
Der Eigenzustand mit J = j1 + j2 und M = J lässt sich sofort in der Produktbasis angeben (nur ein Clebsch-Gordan-Koeffizient gleich 1, alle anderen Null):
Durch Anwenden des Absteigeoperators
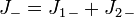 erhält man die Zustände
erhält man die Zustände 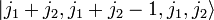 bis
bis 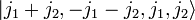 , also zu J = j1 + j2 alle Zustände mit M = − J,...,J = − j1 − j2,...,j1 + j2.
, also zu J = j1 + j2 alle Zustände mit M = − J,...,J = − j1 − j2,...,j1 + j2.Den Zustand
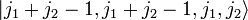 erhält man aus der Forderung nach Orthogonalität zu
erhält man aus der Forderung nach Orthogonalität zu 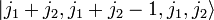 und der Konvention, dass der Clebsch-Gordan-Koeffizient für M = J positiv ist.
und der Konvention, dass der Clebsch-Gordan-Koeffizient für M = J positiv ist.Mit dem Absteigeoperator können zu J = j1 + j2 − 1 wieder alle Zustände mit M = − j1 − j2 + 1,...,j1 + j2 − 1 erzeugt werden. Dieses Verfahren wird nun iterativ wiederholt bis J = | j1 − j2 | .
Weblinks
Tabelle mit Beispielen zu bestimmten Werten für j1 und j2 (PDF, 70 kB)
Literatur
- Wachter, Hoeber: Repetitorium Theoretische Physik. Springer Verlag. ISBN 3540214577
Wikimedia Foundation.