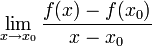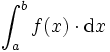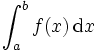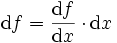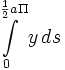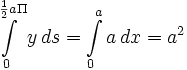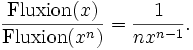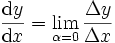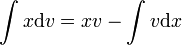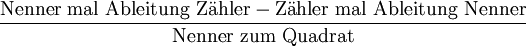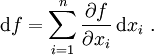- Differenzial (Mathematik)
-
Historisch war der Begriff des Differentials bzw. Differenzials im 17. und 18. Jahrhundert der Kern der Entwicklung der Differentialrechnung. Ab dem 19. Jahrhundert wurde die Analysis durch Augustin Louis Cauchy und Karl Weierstrass auf der Grundlage des Grenzwertbegriffes mathematisch korrekt neu aufgebaut, und der Begriff des Differentials verlor an Bedeutung. Heute taucht die Differentialschreibweise dx noch in folgenden Begriffsbildungen auf:
- Der Differentialquotient, auch Ableitung genannt, und sein höherdimensionales Analogon, das (totale) Differential einer Abbildung (mit dem veränderten zusätzlichen Zeichen
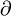 ), auch Ableitung genannt. Sodann tritt er noch in der Variationsableitung oder virtuellen Verschiebung mit dem Zeichen
), auch Ableitung genannt. Sodann tritt er noch in der Variationsableitung oder virtuellen Verschiebung mit dem Zeichen 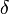 auf.
auf. - In der Integralrechnung
- Differentialoperator
- Differentialformen auf Mannigfaltigkeiten
- Kähler-Differentiale
Im Kontext der letzten beiden Begriffsbildungen hat die Schreibweise dx eine eigenständige Bedeutung.
- In der Physik wird die Schreibweise oft abgekürzt.
- In der historischen Bedeutung des Differentials des 17. bis beginnenden 19. Jahrhunderts, ist der Begriff des Differentials eine endliche Zahlgröße.
Der Differentialquotient
In der Physik veranschaulicht der Begriff der Momentangeschwindigkeit das Differential: Wird beispielsweise ein fallender Körper immer schneller, so muss man zur Erfassung seiner momentanen Geschwindigkeit zu einem bestimmten Zeitpunkt möglichst kleine Zeitintervalle dt betrachten und die entsprechend zurückgelegte Wegstrecke ds messen. Das sind dann eigentlich die Differenzen Δt und Δs. Im Idealfall werden beide Differenzen „unendlich klein“, aber ihr „Quotient“
ist die Momentangeschwindigkeit und kann als Verhältnis endlicher Größen dt und ds geschrieben werden.
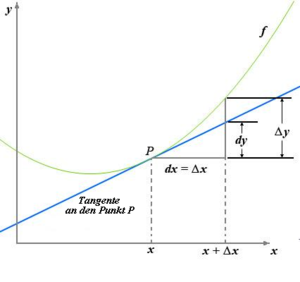
Genau dasselbe Problem tritt auf, wenn man die Steigung der Tangente an einen Funktionsgraphen bestimmen will: sie ist der Quotient, also ein bestimmtes Verhältnis, das beim Grenzwertübergang eingenommen wird, aus der „unendlich kleinen“ Änderung Δf, die der Funktionswert erfährt, und der „unendlich kleinen“ Änderung Δx des Argumentes, dessen Verhältnis mit den endlichen (festen) Größen df und dx wiedergegeben werden kann.
Die moderne, präzise Fassung dieses Begriffes ist der Grenzwert des Differenzenquotienten
Das Differential des Differentialquotienten
Für eine in einem Intervall differenzierbare Funktion f(x) ist die Differenz zwischen Differenzen- und Differentialquotient an der Stelle x0 eine Funktion φ(Δx) von Δx.
Aus
 ergibt sich der Funktionszuwachs
ergibt sich der Funktionszuwachs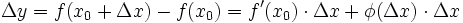 .
.
Er besteht aus einem in Δx linearen Anteil
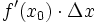 , der von der gleichen Ordnung wie Δx gegen Null konvergiert, und aus einem Anteil
, der von der gleichen Ordnung wie Δx gegen Null konvergiert, und aus einem Anteil  , der für
, der für 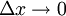 von höherer Ordnung als Δx gegen Null konvergiert. Den linearen Anteil des Zuwachses Δy bezeichnet man als Differential der Funktion an der Stelle x0 und schreibt dafür
von höherer Ordnung als Δx gegen Null konvergiert. Den linearen Anteil des Zuwachses Δy bezeichnet man als Differential der Funktion an der Stelle x0 und schreibt dafür 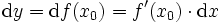 . Die Größe dx = Δx heißt Differential der unabhängigen Variablen. Also Δx ist festgehalten.
. Die Größe dx = Δx heißt Differential der unabhängigen Variablen. Also Δx ist festgehalten.Differentiale in der Integralrechnung
Um den Flächeninhalt eines Bereiches zu berechnen, der von dem Graphen einer Funktion f, der x-Achse und zwei dazu senkrechten Geraden x = a und x = b eingeschlossen wird, unterteilte man die Fläche in Rechtecke der Breite Δx, die „unendlich schmal“ gemacht werden, und der Höhe f(x). Ihr jeweiliger Flächeninhalt ist das „Produkt“
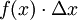 ,
,
der gesamte Flächeninhalt also die Summe
wobei hier dx wieder eine endliche Größe ist, die einer Unterteilung des Intervals [a,b] entspricht. Siehe genauer: Mittelwertsatz der Integralrechnung. Es gibt im Intervall [a,b] einen festen Wert ξ dessen Funktionswert multipliziert mit der Summe der endlichen dx des Intervalls [a,b] den Wert des Integrals wiedergibt:
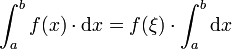
Das Differential des Integrals
Das Differential ist wesentlicher Bestandteil der symbolischen Notation von Integralen und heißt dort Integrationsvariable.
Das Differential dx hinter dem Integral
bezeichnet ein Intervall innerhalb einer Unterteilung von [a;b] (dem Integrationsintervall). Das Gesamtintervall [a;b] des Integrals muss nicht gleichmäßig unterteilt sein. Die Differentiale an den unterschiedlichen Unterteilungsstellen können verschieden groß gewählt sein, die Wahl der Unterteilung des Integrationsintervalls hängt oft von der Art des Integrationsproblems ab. Zusammen mit dem Funktionswert innerhalb des „differentiellen“ Intervalls (beziehungsweise dem Maximal- oder Minimalwert darinnen entsprechend Ober- und Untersumme) bildet sich eine Flächengröße; man macht den Grenzwertübergang in dem Sinne, dass man die Unterteilung von [a;b] immer feiner wählt. Das Integral ist eine Definition für eine Fläche mit Begrenzung durch ein Kurvenstück.
Historisches
Das erste Symbol ist ein stilisiertes S für „Summe“. Leibniz verwendet es das erste Mal in der handschriftlichen Abhandlung Analysis tetragonistica von 1675. „Utile erit scribi
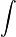 pro omnia“ (Es wird nützlich sein
pro omnia“ (Es wird nützlich sein 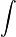 anstatt omnia zu schreiben). Omnia steht dabei für omnia l und wird in dem geometrisch orientierten Flächenberechnungsverfahren von Bonaventura Cavalieri verwendet. Die zugehörige gedruckte Veröffentlichung Leibniz' ist De geometria recondita von 1686, und die Bezeichnungsweise war notwendig, ebenso wie das vorherige
anstatt omnia zu schreiben). Omnia steht dabei für omnia l und wird in dem geometrisch orientierten Flächenberechnungsverfahren von Bonaventura Cavalieri verwendet. Die zugehörige gedruckte Veröffentlichung Leibniz' ist De geometria recondita von 1686, und die Bezeichnungsweise war notwendig, ebenso wie das vorherige 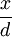 in dx umzuwandeln, um die Rechnung kalkülmäßig einfach und zwangsläufig zu machen.[1]
in dx umzuwandeln, um die Rechnung kalkülmäßig einfach und zwangsläufig zu machen.[1]Es kommt im totalen Differential in der erweiterten Differentialrechnung wieder eine "echte" Summe Σ, dem griechischen Zeichen für S, verbunden mit Differentialen in verschiedenen Zusammenhängen vor.
In der modernen Fassung dieses Zugangs zur Integralrechnung nach Bernhard Riemann ist das „Integral“ ein Grenzwert der Flächeninhalte endlich vieler Rechtecke endlicher Breite für immer feinere Unterteilungen des „x-Bereichs“.
Differentialformen
Differentialformen fassen die folgende Überlegung in eine mathematische Form: Wie schnell sich der Wert einer Funktion f ändert, hängt davon ab, wie schnell sich das Argument ändert. Eine Differentialform df ist also etwas, das ausgehend von einer Änderungsrate x des Arguments (einem Tangentialvektor) angibt, wie rasch sich die Werte von f ändern, wenn man sich so schnell und in die Richtung bewegt, wie x angibt.
In diesem Kontext ist beispielsweise auch die Gleichung
korrekt.
Formal gesehen ist dies nichts anderes als der Begriff der Totalableitung, aber die Sichtweise ist eine andere.
Kähler-Differentiale
Aus der Beobachtung der Differentialgeometrie heraus, dass Tangentialvektoren Derivationen des Raumes der differenzierbaren Funktionen auf einer Mannigfaltigkeit sind, entwickelte sich der Begriff der Kähler-Differentiale: Differentiale werden hier darüber definiert, „dual“ zu den Derivationen zu sein.
Ordnung der Differentiale
Die Differentiale lassen sich auch einfach und übersichtlich in ihrer Ordnung darstellen, jedoch unterschiedlich nach ihrer Abhängigkeit. So steht dx2 für das Differential zweiter Ordnung (entsprechend zweiter Ableitung) der unabhängigen Variable und bedeutet
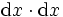 und d2y (auch als ddy und dy' geschrieben) für das Differential zweiter Ordnung der abhängigen Variable, das nicht das Quadrat des Differentials dy ist, sondern das aus einem Differential erneut gebildete Differential. Für dieses Differential gelten die unten angegebenen Rechenregeln.
und d2y (auch als ddy und dy' geschrieben) für das Differential zweiter Ordnung der abhängigen Variable, das nicht das Quadrat des Differentials dy ist, sondern das aus einem Differential erneut gebildete Differential. Für dieses Differential gelten die unten angegebenen Rechenregeln.Erklärung des Differentials zweiter Ordnung d2y
Denkt man sich jetzt h = dx = Δx irgendwie gewählt, und zwar denselben Wert h für verschiedene x, also Δx festgehalten, so wird dy = hf'(x) eine Funktion von x und man kann von ihr wieder ein Differential bilden (s. Abb).
Man kann für d2y = df(x) dann formal schreiben: Für dx = h und h derselbe Wert für verschiedene x, ist diese Größe der lineare Anteil des Zuwachses hf'(x + h) − hf'(x), das heißt, es wird d2y = h2f''(x). Für höhere Ableitungen gilt dies respektive: Z. B. d3y = h3f'''(x)
Historisches
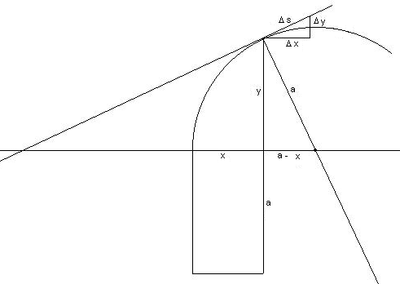
Blaise Pascals Betrachtungen zum Viertelkreisbogen: Quarts de Cercle
Als Gottfried Wilhelm Leibniz als junger Mann 1673 in Paris war, empfing er eine entscheidende Anregung durch eine Betrachtung Pascals in dessen 1659 erschienener Schrift Traité des sinus des quarts de cercle (Abhandlung über den Sinus des Viertelkreises). Er sagt, er habe darin ein Licht gesehen, das der Autor nicht bemerkt habe. Es handelt sich um folgendes (mit modernen Zeichen geschrieben, siehe Abbildung): Um das statische Moment
des Viertelkreisbogens bezüglich der x- Achse zu bestimmen[2], schließt Pascal aus der Ähnlichkeit der Dreiecke
- Δx,Δy,Δs
und
- y,(a − x),a,
dass sich verhalten
- Δs:a = Δx:y,
also
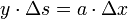 ,
,
so dass
Leibniz bemerkte nun - und dies war das „Licht“, das er sah - , dass dieses Verfahren nicht auf den Kreis beschränkt ist, sondern allgemein für jede (glatte) Kurve gilt, sofern der Kreisradius a durch die Länge der Kurvennormalen (die reziproke Krümmung, der Radius des Krümmungskreises) ersetzt wird. Das infinitesimale Dreieck
- Δx,Δy,Δs
ist das berühmte "charakteristische Dreieck" (Es findet sich auch bei Isaac Barrow zur Tangentenbestimmung[5]). Es ist sehr bemerkenswert, dass die spätere Leibniz'sche Symbolik der Differentialrechnung (dx, dy, ds) gerade dem Standpunkt dieser „verbesserten Indivisibilienvorstellung“ entspricht.[6]
Ähnlichkeit
Alle Dreiecke aus einem Abschnitt Δs der Tangente zusammen mit den zur jeweiligen x-und y-Achse parallelen Stücken Δx und Δy bilden mit dem Dreieck aus Krümmungskreisradius a, Subnormaler x − a und Ordinate y ähnliche Dreiecke und behalten deren Verhältnisse entsprechend der Steigung der Tangente an den Krümmungskreis in diesem Punkt auch bei, wenn der Grenzwertübergang gemacht wird. Das Verhältnis von
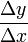 ist ja genau die Steigung von Δs. Deshalb kann man für jeden Krümmungskreis an einem Punkt der Kurve dessen (charakteristische) Proportionen im Koordinatensystem auf die Differentiale dort übertragen, insbesondere wenn sie als infinitesimale Größen aufgefasst werden.[7]
ist ja genau die Steigung von Δs. Deshalb kann man für jeden Krümmungskreis an einem Punkt der Kurve dessen (charakteristische) Proportionen im Koordinatensystem auf die Differentiale dort übertragen, insbesondere wenn sie als infinitesimale Größen aufgefasst werden.[7]acta eruditorum
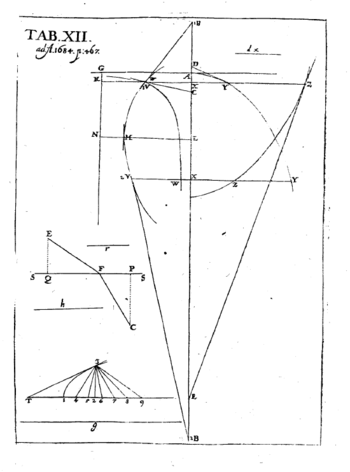
- G. G. L. Nova Methodus Pro Maximis & minimis, itemque tangentibus, …, acta eruditorum, 1684 [8]
- Neue Methode der Maxima, Minima sowie der Tangenten, die sich weder an gebrochenen, noch an irrationalen Größen stößt, und eine eigentümliche darauf bezügliche Rechnungsart. (acta eruditorum 1684)
Gegeben sei eine Achse AX und mehrere Kurven wie VV,WW,YY,ZZ. Ihre zur Achse senkrechten Ordinaten, VX,WX,YX,ZX mögen bezüglich v,w,y,z heißen. Der Abschnitt AX auf der Achse möge x heißen. VB,WC,YD,ZE seien die Tangenten und B,C,D,E ihre bezüglichen Schnittpunkte mit der Achse. Nun wähle man nach Belieben eine Strecke und nenne sie dx. Dann soll diejenige Strecke welche sich zu dx verhält wie v (oder w oder y oder z) zu XB (oder XC oder XD oder XE) mit dv (oder dw oder dy oder dz) bezeichnet werden und Differenz der v (oder w oder y oder z) heißen. Nach diesen Festsetzungen werden die Rechenregeln folgende sein.
Wenn a eine gegebene konstante Größe ist, so wird da gleich 0 und d(ax) gleich adx. Wenn y gleich v ist (d. h. jede Ordinate der Kurve YY gleich der entsprechenden Ordinate der Kurve VV), so wird dy gleich dv. Nun Addition und Subtraktion: Wenn z − y + w + x gleich v ist, so wird d(z − y + w + x) oder dv gleich dz − dy + dw + dx. Multiplikation: d(xv) ist gleich xdv + vdx, das heißt wenn man y gleich xv setzt, so wird dy gleich xdv + vdx. Es ist nämlich gleichgültig, ob man den Ausdruck xv oder als Abkürzung dafür den Buchstaben y anwendet. Zu beachten ist, dass bei dieser Rechnung x und dx in derselben Weise behandelt werden wie y und dy oder ein anderer unbestimmter Buchstabe mit seinem Differential. Zu beachten ist auch, dass es nur mit einer gewissen Vorsicht eine Rückkehr von der Differentialgleichung gibt: darüber werden wir an einer anderen Stelle reden. Nun zur Division
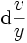 oder (wenn z gleich
oder (wenn z gleich 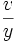 gesetzt wird) dz ist gleich
gesetzt wird) dz ist gleich 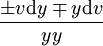 . Was die Zeichen anbetrifft so ist folgendes wohl zu beachten. Wenn bei der Rechnung für einen Buchstaben einfach sein Differential eingesetzt wird, so werden dieselben Zeichen beibehalten, und für + z wird + dz, für − z wird − dz geschrieben, wie aus der eben vorhin behandelten Addition und Subtraktion erhellt. Schreitet man aber zur Entwicklung der Werte, das heißt betrachtet man die Beziehung von z zu x, dann kommt es zum Vorschein, ob der Wert von dz eine positive Größe ist oder kleiner als Null, das heißt negativ. Tritt der letztere Fall ein, dann wird die Tangente ZE vom Punkte Z aus nicht nach A hin gezogen, sondern in der entgegengesetzten Richtung, die von X nach unten weist; dies findet statt, wenn die Ordinaten z mit zunehmenden x abnehmen. Und da die Ordinaten v bald zunehmen, bald abnehmen, so wird dv bald positiv, bald negativ sein. Im ersten falle wird die Tangente V1B1 nach A hin, im zweiten V2B2 nach der entgegengesetzten Seite gezogen. Keins von beiden gilt aber an der Zwischenstelle M, in dem Augenblick, wo die v weder zunehmen noch abnehmen, sondern im Stillstand begriffen sind. dv wird alsdann gleich 0, und es kommt nicht darauf an, ob die Größe positiv oder negativ ist; denn + 0 ist gleich − 0. An dieser Stelle ist v, das heißt die Ordinate LM, ein Maximum (oder, wenn die konvexe Seite der Achse zugekehrt ist ein Minimum), und die Tangente der Kurve in M wird weder in der Richtung von X nach A hinauf gezogen, um sich der Achse zu nähern, noch auch in der entgegengesetzten Richtung, die von X nach unten weist; sie ist vielmehr parallel zur Achse. Wenn dv in bezug auf dx unendlich ist, dann steht die Tangente senkrecht auf der Achse, das heißt sie ist Ordinate. Wenn dv und dx gleich sind, so bildet die Tangente mit der Achse einen halben rechten Winkel. Wenn bei zunehmenden Ordinaten auch ihre Inkremente oder Differenzen dv zunehmen (d. h. wenn bei positiv gesetztem dv auch die ddv, die Differenzen der Differenzen, positiv sind oder bei negativ gesetztem dv auch die ddv negativ), so kehrt die Kurve der Achse ihre konvexe Seite, sonst ihre konkave Seite zu. Wo aber das Inkrement ein Maximum oder Minimum ist, also die Inkremente aus abnehmenden zunehmende werden oder umgekehrt, da ist ein Wendepunkt, und Konkavität und Konvexität vertauschen sich, vorausgesetzt, dass nicht auch die Ordinaten dort aus zunehmenden abnehmende werden oder umgekehrt; dann würde nämlich die Konkavität oder Konvexität bleiben. Dass aber die Inkremente fortfahren zuzunehmen oder abzunehmen, die Ordinaten jedoch aus zunehmenden abnehmende werden oder umgekehrt, das ist unmöglich. (hier irrt sich Leibniz) Ein Wendepunkt ist daher vorhanden, wenn weder v, noch dv gleich 0 ist, wohl aber ddv gleich 0. Deshalb hat auch das Problem d es Wendepunktes nicht wie das Problem des Maximums zwei, sondern gleich drei Wurzeln. Dies alles hängt vom richtigen Gebrauch der Zeichen ab.
. Was die Zeichen anbetrifft so ist folgendes wohl zu beachten. Wenn bei der Rechnung für einen Buchstaben einfach sein Differential eingesetzt wird, so werden dieselben Zeichen beibehalten, und für + z wird + dz, für − z wird − dz geschrieben, wie aus der eben vorhin behandelten Addition und Subtraktion erhellt. Schreitet man aber zur Entwicklung der Werte, das heißt betrachtet man die Beziehung von z zu x, dann kommt es zum Vorschein, ob der Wert von dz eine positive Größe ist oder kleiner als Null, das heißt negativ. Tritt der letztere Fall ein, dann wird die Tangente ZE vom Punkte Z aus nicht nach A hin gezogen, sondern in der entgegengesetzten Richtung, die von X nach unten weist; dies findet statt, wenn die Ordinaten z mit zunehmenden x abnehmen. Und da die Ordinaten v bald zunehmen, bald abnehmen, so wird dv bald positiv, bald negativ sein. Im ersten falle wird die Tangente V1B1 nach A hin, im zweiten V2B2 nach der entgegengesetzten Seite gezogen. Keins von beiden gilt aber an der Zwischenstelle M, in dem Augenblick, wo die v weder zunehmen noch abnehmen, sondern im Stillstand begriffen sind. dv wird alsdann gleich 0, und es kommt nicht darauf an, ob die Größe positiv oder negativ ist; denn + 0 ist gleich − 0. An dieser Stelle ist v, das heißt die Ordinate LM, ein Maximum (oder, wenn die konvexe Seite der Achse zugekehrt ist ein Minimum), und die Tangente der Kurve in M wird weder in der Richtung von X nach A hinauf gezogen, um sich der Achse zu nähern, noch auch in der entgegengesetzten Richtung, die von X nach unten weist; sie ist vielmehr parallel zur Achse. Wenn dv in bezug auf dx unendlich ist, dann steht die Tangente senkrecht auf der Achse, das heißt sie ist Ordinate. Wenn dv und dx gleich sind, so bildet die Tangente mit der Achse einen halben rechten Winkel. Wenn bei zunehmenden Ordinaten auch ihre Inkremente oder Differenzen dv zunehmen (d. h. wenn bei positiv gesetztem dv auch die ddv, die Differenzen der Differenzen, positiv sind oder bei negativ gesetztem dv auch die ddv negativ), so kehrt die Kurve der Achse ihre konvexe Seite, sonst ihre konkave Seite zu. Wo aber das Inkrement ein Maximum oder Minimum ist, also die Inkremente aus abnehmenden zunehmende werden oder umgekehrt, da ist ein Wendepunkt, und Konkavität und Konvexität vertauschen sich, vorausgesetzt, dass nicht auch die Ordinaten dort aus zunehmenden abnehmende werden oder umgekehrt; dann würde nämlich die Konkavität oder Konvexität bleiben. Dass aber die Inkremente fortfahren zuzunehmen oder abzunehmen, die Ordinaten jedoch aus zunehmenden abnehmende werden oder umgekehrt, das ist unmöglich. (hier irrt sich Leibniz) Ein Wendepunkt ist daher vorhanden, wenn weder v, noch dv gleich 0 ist, wohl aber ddv gleich 0. Deshalb hat auch das Problem d es Wendepunktes nicht wie das Problem des Maximums zwei, sondern gleich drei Wurzeln. Dies alles hängt vom richtigen Gebrauch der Zeichen ab.Manchmal aber sind, wie vorhin bei der Division, zweideutige Zeichen anzuwenden, bevor es nämlich feststeht, wie sie entwickelt werden sollen. Und zwar müssen, wenn mit zunehmenden x die
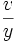 zunehmen (abnehmen), die zweideutigen Zeichen
zunehmen (abnehmen), die zweideutigen Zeichen 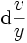 in, das heißt in
in, das heißt in 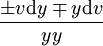 so entwickelt werden, dass dieser Bruch eine positive (negative) Größe wird. Es bedeutet aber
so entwickelt werden, dass dieser Bruch eine positive (negative) Größe wird. Es bedeutet aber 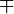 das Entgegengesetzte von
das Entgegengesetzte von 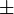 , so dass, wenn dieses + ist, jenes − oder umgekehrt. Es können auch in derselben Rechnung mehrere Zweideutigkeiten vorkommen, die ich durch Klammern unterscheide. Wenn z. B.
, so dass, wenn dieses + ist, jenes − oder umgekehrt. Es können auch in derselben Rechnung mehrere Zweideutigkeiten vorkommen, die ich durch Klammern unterscheide. Wenn z. B.
wäre, so würde sein
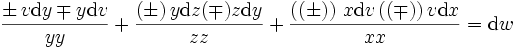
sein, damit nicht die von den verschiedenen Gliedern herrührenden Zweideutigkeiten vermischt werden. Dabei ist zu beachten, dass ein zweideutiges Zeichen mit sich selbst + gibt, mit seinem entgegengesetzten −, während es mit anderen eine neue Zweideutigkeit bildet, die von beiden abhängt. Potenzen:

Z. B. ist
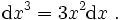
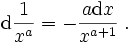
Z. B. wird, wenn

ist,
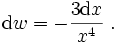
Wurzeln:
![{\rm d}\sqrt[b]{x^a} = \frac {a} {b} {\rm d} x \; \sqrt[b]{x^{a-b}}.](/pictures/dewiki/55/7e2260e4fdd99c68ed7716cc7ff5a604.png)
(Hieraus folgt
![{\rm d}\sqrt[2]{y} = \frac {{\rm d}y} {2\sqrt[2]{y}}\;;](/pictures/dewiki/101/ea346e888834d7aa431514892d1de40a.png)
denn a ist in diesem Falle 1, und b ist 2, also
![\frac {a}{b}\sqrt[b]{x^{a-b}}](/pictures/dewiki/49/13b92600aa4d50d4453f9f9b8510393b.png)
gleich
![\frac {1} {2} \sqrt[2]{y^{-1}}\;;](/pictures/dewiki/51/3d08941dac9db09d102cbe036d9eeed2.png)
nun ist y − 1 dasselbe wie
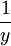 nach der Natur der Exponenten einer geometrischen Reihe, und
nach der Natur der Exponenten einer geometrischen Reihe, und ![\sqrt[2]{\frac{1} {y}},](/pictures/dewiki/101/eb031adf030cee66eccb7720960f2cc6.png) ist
ist ![\frac{1} {\sqrt[2]{ y}}\;.](/pictures/dewiki/98/b6ca2fbee21503db54f2fa9cbe0083a4.png) )
)![{\rm d}\frac{1} {\sqrt[b]{x^a}} = - \frac {a{\rm d} x} {b\sqrt[b]{x^{a+b}}} \;.](/pictures/dewiki/55/7d613fa80b86fbb68a31c2b2f5cde754.png) [9]
[9]Es hätte aber die Regel der ganzen Potenz genügt, um sowohl die Brüche als auch die Wurzeln zu erledigen; denn eine Potenz wird ein Bruch, wenn der Exponent negativ ist, und sie verwandelt sich in eine Wurzel, wenn der Exponent gebrochen ist. Ich habe aber jene Folgerungen lieber selbst gezogen, als sie anderen zu ziehen überlassen, da sie sehr allgemein sind und häufig vorkommen. Auch ist es bei einer an sich verwickelten Sache besser, für Leichtigkeit zu sorgen. Kennt man, wenn ich so sagen soll, den obigen Algorithmus dieses Kalküls, den ich Differentialrechnung nenne, so lassen sich alle anderen Differentialgleichungen durch ein gemeinsames Rechnungsverfahren finden, es lassen sich die Maxima und Minima sowie die Tangenten erhalten, ohne dass es dabei nötig ist, Brüche oder Irrationalitäten oder andere Verwicklungen zu beseitigen, was nach den bisher bekannt gegebenen Methoden doch geschehen musste, Der Beweis alles dessen wird für einen in diesen Dingen Erfahrenen leicht sein, wenn er nur den bisher nicht genug erwogenen Umstand beachtet, dass man dx,dy,dv,dw,dz als proportional zu den augenblicklichen Differenzen, das heißt Inkrementen oder Dekrementen der x,y,v,w,z (eines jeden in seiner Reihe) betrachten kann. So kommt es, dass man zu jeder vorgelegten Gleichung ihre Differentialgleichung aufschreiben kann. Dies geschieht indem man für jedes Glied (d. h. jeden Bestandteil, der durch bloße Addition oder Subtraktion zur Herstellung der Gleichung beiträgt) einfach das Differential des Gliedes einsetzt, für eine andere Größe jedoch (die nicht selbst ein Glied ist, sondern zur Bildung eines Gliedes beiträgt) ihr Differential anwendet, um das Differential des Gliedes selbst zu bilden, und zwar nicht ohne weiteres,sondern nach dem oben vorgeschriebenen Algorithmus. Die bisher bekannt gemachten Methoden haben aber einen solchen Übergang nicht. Sie wenden nämlich meistens eine Strecke wie DX oder eine andere von dieser Art an, nicht aber die Stecke dy, die die vierte Proportionale zu DX,DY,dx ist, und dadurch wird alles verwirrt. Daher schreiben sie vor, dass Brüche und Irrationalitäten (worin Unbestimmte vorkommen) zuvor beseitigt werden. Es ist auch klar, dass unsere Methode die transzendenten Linien beherrscht, die sich nicht auf die algebraische Rechnung zurückführen lassen oder von keinem bestimmten Grade sind, und zwar gilt das ganz allgemein, ohne besondere nicht immer zutreffende Voraussetzungen, Man muss nur ein für allemal festhalten, dass eine Tangente zu finden so viel ist wie eine Gerade zeichnen, die zwei Kurvenpunkte mit unendlich kleiner Entfernung verbindet, oder eine verlängerte Seite des undendlicheckigen Polygons, welches für uns mit der Kurve gleichbedeutend ist. Jene unendlich kleine Entfernung lässt sich aber immer durch irgendein bekanntes Differential, wie dv, oder durch eine Beziehung zu demselben ausdrücken, das heißt durch eine gewisse bekannte Tangente. Wäre insbesondere y eine transzendente Größe, zum Beispiel die Ordinate der Zykloide und käme sie in der Rechnung vor, mit deren Hilfe z, die Ordinate einer anderen Kurve bestimmt wäre, und verlangte man dz oder durch dessen Vermittlung die Tangente der zweiten Kurve, so wäre unter allen Umständen dz durch dy zu bestimmen, weil man die Tangente der Zykloide hat. Die Tangente der Zykloide selbst aber ließe sich, wenn wir annehmen, dass wir sie noch nicht hätten, in ähnlicher Weise durch Rechnung finden aus der gegebenen Eigenschaft der Kreistangenten…[10]
Es folgen ein formales Beispiel, ein dioptrisches der Lichtbrechung, eines, das den Satz von Pythagoras nutzt, und eines, das den Logarithmus behandelt.
Notiz von Newton
Hier noch eine aufschlussreiche Notiz von Newton: (Abhandlung über die Quadratur der Kurven, 1704, 10. Absatz):
Die Größe x möge gleichförmig fließen, und es sei die Fluxion (das Differential df)der Größe xn zu finden. In der Zeit, in der x beim Fließen zu x + o wird, wird xn zu (x + o)n(o bedeutet bei Newton das infinitesimale Δx oder in moderner Notation h, allerdings ist bei ihm durch den Begriff des Fließens das Zeitliche eingegangen und es ist die unabhängige Variable nicht x sondern t und so kommt sein Differential dt} zustande.) d. h. nach der Methode der unendlichen Reihen zu
Die Zunahmen
- o und

verhalten sich zueinander wie:
- 1 und

Nun mögen jene Zunahmen verschwinden. Dann wird ihr letztes Verhältnis
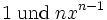 sein. Es verhält sich daher die Fluxion der Größe x (das Differential dx oder dt) zu der Fluxion der Größe xn wie 1 zu nxn − 1. Oder:
sein. Es verhält sich daher die Fluxion der Größe x (das Differential dx oder dt) zu der Fluxion der Größe xn wie 1 zu nxn − 1. Oder:Cauchys Differentialbegriff
In den 1980er Jahren fand in Deutschland eine Auseinandersetzung statt, inwieweit die Grundlegung der Analysis bei Cauchy logisch einwandfrei ist. Detlef Laugwitz versucht mit Hilfe einer historischen Lesart Cauchys, den Begriff unendlich kleiner Größen für seine Ω Zahlen fruchtbar zu machen, findet aber daraus resultierend bei Cauchy Unstimmigkeiten. Detlef Spalt korrigiert den (ersten!) historischen Lesansatz der cauchyschen Arbeiten und fordert die Verwendung von Begriffen aus Cauchys Zeit und nicht heutigen Begriffen zum Nachweis seiner Sätze und kommt zu dem Ergebnis, dass Cauchys Grundlegung der Analysis logisch einwandfrei ist, jedoch bleiben weiterhin die Fragen nach der Behandlung unendlich kleiner Größen offen.
Die Differentiale bei Cauchy sind endlich und konstant dx = h (h endlich). Der Wert der Konstanten ist nicht näher bestimmt.
Δx ist bei Cauchy unendlich klein und veränderlich.
Die Beziehung zu h ist Δx = i = αh, wobei h endlich und α infinitesimal (unendlich klein) ist.
Ihr geometrisches Verhältnis ist als
bestimmt. Dieses Verhältnis unendlich kleiner Größen, oder genauer die Grenze geometrischer Differenzenverhältnisse abhängiger Zahlgrößen, einen Quotienten, kann Cauchy auf endliche Größen übertragen.
Differentiale sind endliche Zahlgrößen, deren geometrische Verhältnisse streng gleich den Grenzen der geometrischen Verhältnisse sind, welche aus den unendlich kleinen Zuwächsen der vorgelegten unabhängigen Veränderlichen oder der Veränderlichen der Funktionen gebildet sind. Cauchy hält es für wichtig Differentiale als endliche Zahlgrößen zu betrachten.
Der Rechner bedient sich der Unendlich kleinen als Vermittelnden, welche ihn zu der Kenntnis der Beziehung führen müssen, die zwischen den endlichen Zahlgrößen bestehen; und nach Cauchys Meinung dürfen die Unendlich kleinen in den Schlussgleichungen, wo ihre Anwesenheit sinnlos, zwecklos und nutzlos bliebe, nie zugelassen werden. Außerdem: Wenn man die Differentiale als beständig sehr kleine Zahlgrößen betrachtete, dann gäbe man dadurch den Vorteil auf, der darin besteht, dass man unter den Differentialen von mehreren Veränderlichen das eine als Einheit nehmen kann. Denn um eine klare Vorstellung einer beliebigen Zahlgröße auszubilden, ist es wichtig, sie auf die Einheit ihrer Gattung zu beziehen. Es ist also wichtig, unter den Differentialen eine Einheit auszuwählen.
Insbesondere fällt für Cauchy die Schwierigkeit weg, höhere Differentiale zu definieren. Denn Cauchy setzt dx = h nachdem er die Rechenregeln der Differentiale durch Übergang zu den Grenzen erhalten hat. Und da das Differential einer Funktion der Veränderlichen x eine andere Funktion dieser Veränderlichen ist, kann er y mehrmals differenzieren und erhält in dieser Weise die Differentiale verschiedener Ordnungen.
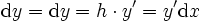
- ddy = d2y = hdy' = y''h2
- dddy = d3y = h2dy'' = y'''h3
- …
Anmerkung 1
Leibniz wählt die Einheit, indem er dx = const. und ddx = 0 setzt. [12]
Anmerkung 2
Genauso wird, wenn man x mit der identischen Funktion identifiziert, das Differential von x die „Einheit“. Ist f'(x) die Ableitung der Funktion f, so ist die lineare Funktion
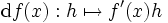 das Differential von f an der Stelle x.
das Differential von f an der Stelle x.
Also für
 ist insbesondere d(f(x(h)) = dx(h) = h weshalb die Schreibweise
ist insbesondere d(f(x(h)) = dx(h) = h weshalb die Schreibweise- df(x) = f'(x)dx
oder
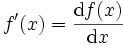 und die Bezeichnung Differentialquotient berechtigt sind.
und die Bezeichnung Differentialquotient berechtigt sind.
Notation
Differential der unabhängigen Variable
Sei x die unabhängige Variable, so gilt für das Differential von x:
- dx = konst.
- ddx = 0. (ddx steht für d(dx), das Differential des Differentials)
Die Bezeichnung der Variable ist beliebig. Newton nennt sie t. Man kann aber auch z oder y nehmen und muss dann dabei bleiben.
Konstante und konstanter Faktor
- d(konst.) = 0; und
- d(ax) = adx ; a ist konstant, weswegen xda = 0 (d. i. eine Hälfte der Produktregel unter Multiplikation.)
Addition und Subtraktion
Wenn z − y + w + x gleich v ist, so wird
- dv = d(z − y + w + x) = dz − dy + dw + dx.
Multiplikation
Vergleiche die Darstellung unter Division.
d(xv) ist gleich xdv + vdx

Partielle Integration
Von hier kommt man zur partiellen Integration, indem man diese „Produktregel“ umschreibt:
- d(xv) = xdv + vdx
- xdv = d(xv) − vdx
und integriert:
Wobei hier x nicht unbedingt die unabhängige Variable sein muss, weil sonst dx = konst. und somit nur eingeschränkt x' ist.
Division
Vergleiche die Darstellung unter Multiplikation.
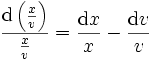
Wir setzen
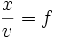
somit
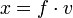
Und nach der Produktregel:
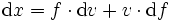
womit
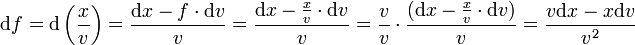
In Form einer Schulregel:
Kettenregel
Die verschachtelten Funktionen
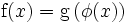 und deren Ableitung
und deren Ableitung 
werden in der suggestiven Leibniz'schen Bezeichnung zu:
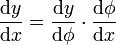
Notationen der Ableitung
Verantwortlicher 1. Ableitung 2. Ableitung n-te Ableitung Bemerkung Newton 
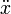
heutzutage wird diese Schreibweise für die n-te Ableitung nach der Zeit in der Physik verwendet, sowie für eine koordinatenunabhängige Parameterdarstellung. Leibniz 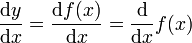

oder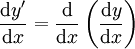
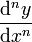 etc.
etc.Die Klammern um (dx)2 = dx2 werden weggelassen. Lagrange y' = f'(x) (sprich: f Strich von x) y'' = f''(x) (sprich: f Zweistrich von x) f(n)(x) Man sieht die funktionale Abhängigkeit. Cauchy Df(x) (D)(2)f(x) (D)(n)f(x) D heißt Derivierte (besonders im englischsprachigen Raum) Erweiterung und Varianten
Anstatt d finden sich folgende Symbole, die Differentiale bezeichnen:
- Mit
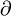 wird ein partielles Differential bezeichnet
wird ein partielles Differential bezeichnet - Mit δ (dem griechischen kleinen Delta) wird eine virtuelle Verschiebung, die Variation eines Ortsvektors bezeichnet. Sie hängt also mit dem partiellen Differential nach den einzelnen Raumdimensionen des Ortsvektors zusammen.
Virtuelle Verschiebung, Variationsableitung
Mathematisch gesprochen werden bei einer virtuellen Verschiebung die Ortskoordinaten des physikalischen Systems bei festgehaltener Zeit t variiert. Die Variation des Ortsvektors
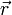 , also die virtuelle Verschiebung des betreffenden Systempunkts ist
, also die virtuelle Verschiebung des betreffenden Systempunkts ist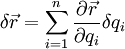 .
.
Das Symbol wird also für die Variationsableitung benutzt.
Totales Differential
Dieselbe Mischform verschiedener Differentiale und einer Summe anstatt eines Integralzeichens weist auch das totale Differential oder vollständige Differential auf:
Der Vektor oben wird als Funktion aufgefasst.
Quellen
- ↑ K. Popp, E. Stein, Gottfried Wilhelm Leibniz. Philosoph, Mathematiker, Physiker, Techniker. Schlütersche, Hannover 2000, ISBN 3-87706-609-7 S. 50
- ↑ Bei konstanter Dichte deckt sich die Teilmasse mν mit dem Bogen Δs an dieser Stelle und ds entsprechend.
- ↑ Anm.: Hier wird genau
 integriert. Lösung:
integriert. Lösung: ![[a \cdot x]_{0}^{a}](/pictures/dewiki/52/45f658c980135a3ab77325f9a6885e65.png) .
. - ↑
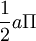 ist die Grenze für die Unabhängige s, a die entsprechend umgerechnete für den „Parameter“ x. Man sieht auch anschaulich in der Abbildung, dass man mit dem Viertelbogen eine Radiuslänge auf der x-Achse durchläuft und umgekehrt.
ist die Grenze für die Unabhängige s, a die entsprechend umgerechnete für den „Parameter“ x. Man sieht auch anschaulich in der Abbildung, dass man mit dem Viertelbogen eine Radiuslänge auf der x-Achse durchläuft und umgekehrt. - ↑ Eintrag Zeno.org
- ↑ Oskar Becker, Grundlagen der Mathematik, suhrkamp
- ↑ Reinhard Finster, Gerd van der Heuvel, Gottfried Wilhelm Leibniz, Monographie, Rowohlt
- ↑ Differenz heißt auf Latein differentia und differentiell differentialis. Vielleicht entsteht die Verwirrung der Begriffe auch wegen dieser sprachlichen Ähnlichkeit.
- ↑ Das lateinische Original enthält hier einen Rechen- oder Druckfehler: a und b in Zähler und Nenner sind vertauscht.
- ↑ a b Gottfried Leibniz, Sir Isaac Newton: Über die Analysis des Unendlichen – Abhandlung über die Quadratur der Kurven. Ostwalds Klassiker der exakten Wissenschaften, Band 162, Verlag Harri Deutsch, ISBN 3-8171-3162-3 Copyright
- ↑ Detlef Spalt: Die Vernunft im Cauchy-Mythos. Verlag Harri Deutsch, ISBN 3-8171-1480-X (zu modernen Begriffsproblemen, und ob Cauchy es nun verstanden hat oder nicht, und einiges andere, unter anderem virtuelle Diskussionen mit verstorbenen Mathematikern Abel etc.)
- ↑ Henk Bos: Differentials, Higher-Order Differentials and the Derivative in the Leibnizian Calculus. Archive for History of Exact Sciences 14, 1–90.
- ↑ Duden, Rechnen und Mathematik. Bibliographisches Institut, ISBN 3-411-02423-2.
Literatur
- Gottfried Leibniz, Sir Isaac Newton: Über die Analysis des Unendlichen – Abhandlung über die Quadratur der Kurven. Ostwalds Klassiker der exakten Wissenschaften, Band 162, Verlag Harri Deutsch, ISBN 3-8171-3162-3
- Oskar Becker: Grundlagen der Mathematik. Suhrkamp Verlag, ISBN 3-518-07714-7
- Detlef Spalt: Die Vernunft im Cauchy-Mythos. Verlag Harri Deutsch, ISBN 3-8171-1480-X (Spalt problematisiert die Übernahme moderner Begriffe auf frühere Analysis, stellt fest, dass Cauchys Aufbau der Analysis logisch einwandfrei ist, thematisiert benachbarte Begriffe und läßt Cauchy virtuelle Diskussionen mit wesentlich jüngeren Mathematikern führen über deren begriffliche Genauigkeit, z.B. Abel etc.)
- K. Popp, E. Stein (Hrsg.): Gottfried Wilhelm Leibniz, Philosoph, Mathematiker, Physiker, Techniker. Schlütersche GmbH & Co. KG, Verlag und Druckerei, Hannover 2000, ISBN 3-87706-609-7
- Bos, Henk, Differentials, Higher-Order Differentials and the Derivative in the Leibnizian Calculus, Archive for History of Exact Sciences 14, 1–90. Heftig diskutierte Veröffentlichung aus den 1970ern, um Kontinuum und Unendlichkeit.
- Der Differentialquotient, auch Ableitung genannt, und sein höherdimensionales Analogon, das (totale) Differential einer Abbildung (mit dem veränderten zusätzlichen Zeichen
Wikimedia Foundation.