- Differenzierbar
-
Als Differenzierbarkeit bezeichnet man in der Mathematik die Eigenschaft einer Funktion, sich lokal um einen Punkt in eindeutiger Weise linear approximieren zu lassen. Differenzierbarkeit ist in zahlreichen mathematischen Räumen definiert.
Die Differenzierbarkeit gehört zu den Problemstellungen der Differentialrechnung, die ihrerseits ein mathematisches Teilgebiet der Analysis darstellt.
Inhaltsverzeichnis
Definitionen
Reellwertige Funktionen einer reellen Veränderlichen
Im einfachsten Fall betrachtet man eine reellwertige Funktion einer reellen Variablen, also eine Funktion
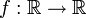 aus der Menge der reellen Zahlen in sich selbst.
aus der Menge der reellen Zahlen in sich selbst.1. Definition: Eine Funktion f ist genau dann differenzierbar an einer Stelle x0 ihres Definitionsbereichs, wenn eine reelle Zahl a und eine Funktion g (Fehler der Approximation) existieren, derart, dass:
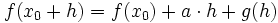
und g von höherer als erster Ordnung gegen 0 geht. (Wachstumsvergleich
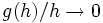 für
für 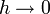 ) Den Wert a bezeichnet man als die Ableitung von f an der Stelle x0.
) Den Wert a bezeichnet man als die Ableitung von f an der Stelle x0.2. Definition: Eine Funktion f ist genau dann differenzierbar an einer Stelle x0 ihres Definitionsbereichs, wenn der Grenzwert
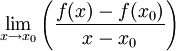 existiert. Diesen Grenzwert bezeichnet man als die Ableitung von f an der Stelle x0.
existiert. Diesen Grenzwert bezeichnet man als die Ableitung von f an der Stelle x0.Beide Definitionen sind äquivalent.
Wenn eine Funktion f an einer Stelle x0 differenzierbar ist, schreibt man für die Ableitung f'(x0) oder auch
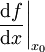 .
.Eine Funktion heißt genau dann differenzierbar (ohne Einschränkung auf einen speziellen Punkt), wenn sie an jeder Stelle ihres Definitionsbereichs differenzierbar ist.
Verallgemeinerung auf komplexe Funktionen
Es sei
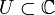 eine offene Teilmenge der komplexen Ebene und
eine offene Teilmenge der komplexen Ebene und 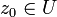 ein Punkt dieser Teilmenge. Eine Funktion
ein Punkt dieser Teilmenge. Eine Funktion 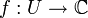 heißt komplex differenzierbar im Punkt z0, falls der Grenzwert
heißt komplex differenzierbar im Punkt z0, falls der Grenzwertexistiert. In diesem Fall bezeichnet man diesen Grenzwert als
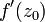 .
.Eine Funktion f heißt holomorph im Punkt z0, falls eine Umgebung von z0 existiert, in der f komplex differenzierbar ist.
Verallgemeinerung auf Funktionen in Banachräumen
Seien
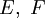 Banachräume und
Banachräume und 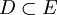 eine offene Menge. Eine Abbildung
eine offene Menge. Eine Abbildung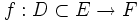 heißt im Punkt
heißt im Punkt 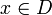 differenzierbar
differenzierbar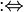
![\exists A\in\mathfrak{L}[E,F],\ \exists r(h),\ \exists\delta>0:\forall h\in E,\ \Vert h\Vert \leq\delta:x+h\in D](/pictures/dewiki/97/a68d7416124bf156984b2f10dcb7d39c.png)
und
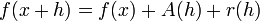
und
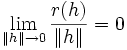
Erläuterungen
Grafisch lässt sich die Eigenschaft Differenzierbarkeit so deuten, dass eine Funktion genau dann differenzierbar ist, wenn an jedem Punkt des Graphen von f genau eine Tangente existiert.
Differenzierbarkeit und Stetigkeit
Eine Funktion, die an einer Stelle differenzierbar ist, ist dort auch stetig. Die Umkehrung dieser Aussage gilt nicht, wie das Beispiel
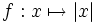 zeigt.
zeigt.Für viele mathematische Sätze ist nicht die Differenzierbarkeit, sondern die stetige Differenzierbarkeit relevant, also die Frage, ob auch die Ableitung selbst noch eine stetige Funktion ist. Von ganz besonders großer Bedeutung sind in diesem Zusammenhang die beliebig oft stetig differenzierbaren oder glatten Funktionen.
Beispiel: Ist
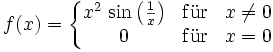 dann ist wegen
dann ist wegen 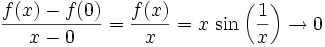 für
für 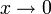
die Ableitung
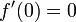 . Und
. Und  ist
ist 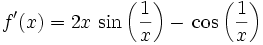 , wobei
, wobei 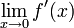 nicht existiert. Die Funktion f ist daher differenzierbar, jedoch nicht stetig differenzierbar.
nicht existiert. Die Funktion f ist daher differenzierbar, jedoch nicht stetig differenzierbar.Eine Trajektorie eines Wiener-Prozesses ist als Funktion
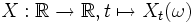 stetig – aber fast sicher nirgends differenzierbar.
stetig – aber fast sicher nirgends differenzierbar.Die nach ihrem Entdecker benannte Weierstraß-Funktion
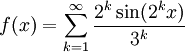 ist ebenfalls überall stetig, aber sogar nirgends differenzierbar.
ist ebenfalls überall stetig, aber sogar nirgends differenzierbar.Begriffserweiterungen
Der Begriff der Differenzierbarkeit lässt sich ausdehnen auf
- mehrdimensionale Räume, in welchen partielle und totale Differenzierbarkeit unterschieden werden müssen.
- komplexe Räume, bei denen die reellen Zahlen durch komplexe Zahlen ersetzt werden; hier liefert Differenzierbarkeit eine wesentlich stärkere Einschränkung einer Funktion
- gekrümmte Räume bzw. differenzierbare Mannigfaltigkeiten und komplexe Mannigfaltigkeiten.
Folgende Konzepte stellen eine Verallgemeinerung der Differenzierbarkeit dar:
- schwache Ableitungen
- Differenzierbarkeit im Sinne von Distributionen
- Fréchet-Ableitung
- Gâteaux-Ableitung
Wikimedia Foundation.