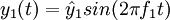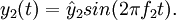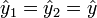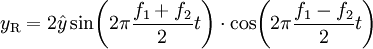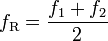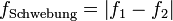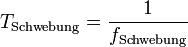- Differenztondämpfungsmaß
-
Als Schwebung bezeichnet man die Resultierende der additiven Überlagerung (Superposition) zweier Schwingungen, die sich in ihrer Frequenz nur wenig voneinander unterscheiden. Schwebungen treten bei allen Wellen auf, für die das Superpositionsprinzip gilt, also beispielsweise Schallwellen und elektromagnetischen Wellen; siehe Differenztonfaktor. Kurz gesagt ist eine Schwebung eine Schwingung mit periodisch veränderlicher Amplitude. Sie entsteht durch Überlagerung von Schwingungen mit ähnlichen Frequenzen, f1 muss ungefähr f2 sein.
Inhaltsverzeichnis
Akustik
In der Akustik ist die Schwebung deutlich zu hören: Erklingen zwei Töne, deren Frequenzen sich nur wenig unterscheiden, so ist ein Ton zu hören, dessen Frequenz dem Mittelwert der Frequenzen der beiden überlagerten Töne entspricht. Dieser Ton ist moduliert, seine Lautstärke schwankt mit der sogenannten Schwebungsfrequenz, die der Differenz der Frequenzen der beiden Töne entspricht.
Übersteigt der Frequenzunterschied etwa fünf Prozent, vernimmt man einen Ton rauer Klangfärbung, der sich bei weiterer Vergrößerung der Frequenzdifferenz in zwei Einzeltöne aufspaltet.
Als kritische Bandbreite wird derjenige Bereich um eine Tonfrequenz f0 bezeichnet, innerhalb dessen die Frequenz eines zweiten Tones liegen muss, damit ein rauer oder schwebender Ton statt zwei getrennter Töne wahrgenommen wird. Die Größe der kritischen Bandbreite hängt von der Frequenz f0 ab: Je kleiner die Frequenz f0 ist, desto größer ist die kritische Bandbreite.
 Klangbeispiel?/i: Dem Grundton von 440 Hz ist ein zweiter Ton überlagert, dessen Frequenz von 440 Hz auf 490 Hz ansteigt.
Klangbeispiel?/i: Dem Grundton von 440 Hz ist ein zweiter Ton überlagert, dessen Frequenz von 440 Hz auf 490 Hz ansteigt.Mathematische Beschreibung
In der folgenden Berechnung ist:
- f1 die Frequenz der Sinus-Schwingung 1,
- f2 die Frequenz der Sinus-Schwingung 2,
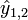 die Amplitude der einzelnen Schwingungen (gleich für 1 und 2),
die Amplitude der einzelnen Schwingungen (gleich für 1 und 2),- t der Zeitpunkt,
- π die Kreiszahl,
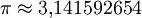
- yR die resultierende Summenschwingung,
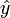 ihre Amplitude,
ihre Amplitude,- fR ihre Frequenz,
- fS die Frequenz einer cosinusförmigen Schwingung, welche die Schwebungsfunktion yR einhüllt,
- fSchwebung die Schwebungsfrequenz.
Man betrachte zwei gleichgerichtete harmonische Schwingungen mit leicht unterschiedlichen FrequenzenZur Vereinfachung sei angenommen, dass beide Schwingungen dieselbe Amplitude haben.
Dann kann die Summenschwingung so dargestellt werden:
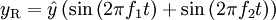 .
.
Dieser Ausdruck kann durch Anwendung der Additionstheoreme umgeformt werden in die folgende Formel:
Die letzte Formel besagt, dass die Frequenz der Überlagerungsschwingung die mittlere Frequenz der beiden Teilschwingungen ist (entspricht dem Sinus-Glied der Formel, siehe fR unten) und dass die resultierende Amplitude sich zeitlich ändert (dies wird durch das Kosinus-Glied ausgedrückt, siehe fS und fSchwebung unten). Es gilt:
Für fS findet man den Ausdruck fS = (f1 − f2) / 2 - dieses ist die Frequenz, die sich rechnerisch aus dem Kosinus-Glied ergibt. Da es für die Umhüllende der Überlagerungsschwingung (d.h. für die hörbare Amplitudenschwankung) egal ist, ob sich der Kosinus im plus- oder minus-Bereich befindet, ist die hörbare Frequenz der Lautstärkeänderung doppelt so groß. Diese so genannte Schwebungsfrequenz ist definiert als
und ihr Betrag ist wesentlich kleiner als fR. Die sich daraus ergebende Schwebungsperiode
ist der zeitliche Abstand zwischen zwei Punkten minimaler Amplitude (Knoten) der Schwebungsfunktion yR.
Unreine Schwebung
Sind die Amplituden der beiden beteiligten Schwingungen nicht gleich, dann spricht man von der so genannten Unreinen Schwebung. Bei dieser ist das entsprechende Kosinus-Glied anders ausgebildet, und es treten keine Stilleperioden (wenn die resultierende Amplitude der reinen Schwebung durch Null geht) auf. Des Weiteren schwankt die Schwingungsdauer, anders ausgedrückt, die resultierende Frequenz (das Sinus-Glied oben) ist nicht konstant.
Weitere Klangbeispiele
Um das Verständnis der akustischen Schwebung etwas zu erleichtern, finden sich hier vier beispielhafte unterschiedliche Schwingungen. Alle besitzen dieselbe Startfrequenz, sie unterscheiden sich jedoch in ihrer Wellenform: Dreieck, Rechteck, Sägezahn, Sinus
In allen vier Klangbeispielen wurden zwei Schwingungen überlagert. Ab Sekunde 4 wurde begonnen, eine dieser Schwingungen langsam in der Frequenz zu erhöhen und sie dann wieder um das Doppelte zu reduzieren. Einen exakten Verlauf stellt folgendes Diagramm dar:
Anwendungen
Das Phänomen der Schwebung kann vielseitig angewendet werden. In der Musizierpraxis wird sie als
- belebender Klangeffekt bei Musikinstrumenten beispielsweise als zuschaltbarer sogenannter Tremoloeffekt oder als spezielles Register in Pfeifenorgeln eingesetzt.
- Das Leslie Lautsprecher-Kabinett verwendet den Doppler-Effekt zur Erzeugung der Schwebung. Hierbei wird der konstante Originalton mit einem in der Tonhöhe vibrierenden Ton überlagert.
- Bei Tremoloharmonikae (Wiener Stimmung) und bei einem Register am Akkordeon erfolgt die Tonerzeugung mit zwei Durchschlagzungen, die in einer Schwebung gestimmt sind.
- Das Stimmen eines Musikinstruments nach Gehör (ohne Stimmgerät mit optischer Anzeige), also das eigentliche Einstimmen auf den Kammerton als Referenzfrequenz, erfolgt solange, bis keine Schwebung mehr zu hören ist: Der Ton ist „schwebungsnull - er stimmt“ .
- Die Tonharmonie des Bambus-Instruments Angklung basiert auf dem Prinzip von zwei bis vier in Schwebung befindlicher Klangkörper (Bässe, Melodieinstrumente und Akkorde), die gleichzeitig geschüttelt werden.
Unangenehm störend wird die Schwebung hingegen, wenn zwei Instrumente mit annähernd sinusförmigen Tönen (Flöten) eng benachbarte Töne spielen - man sagt, die Töne reiben sich.
Mit zwei elektrischen Schwingkreisen können Systeme gebaut werden, die folgenden Effekt nutzen: Ein Schwingkreis erzeugt eine (manuell justierbare,) feste Referenzfrequenz. Ein zweiter Schwingkreis wird über seine Dipolantenne in seiner Frequenz beeinflusst. Beide Frequenzen werden überlagert, die daraus resultierende Schwebung wird weiterverarbeitet. Dies kann wie bei dem
- Theremin ein durch Handbewegungen beeinflusstes Musikinstrument sein.
- Bei Metallsuchgeräten beeinflusst Metall einer bestimmten Masse die Frequenzen,
- bei Überwachungsanlagen mit Bewegungsmeldern wird beispielsweise durch Annäherung eines Menschen das Signal eines Wärmesensors als Stellglied im veränderbaren Schwingkreis ausgenutzt.
Siehe auch
Weblinks
Wikimedia Foundation.