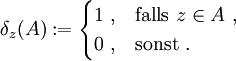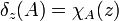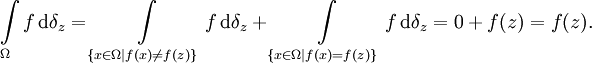Dirac sea — for a massive particle. • particles, • antiparticles The Dirac sea is a theoretical model of the vacuum as an infinite sea of particles with negative energy. It was first postulated by the British physicist Paul … Wikipedia
Dirac delta function — Schematic representation of the Dirac delta function by a line surmounted by an arrow. The height of the arrow is usually used to specify the value of any multiplicative constant, which will give the area under the function. The other convention… … Wikipedia
Dirac large numbers hypothesis — Paul Dirac The Dirac large numbers hypothesis (LNH) is an observation made by Paul Dirac in 1937 relating ratios of size scales in the Universe to that of force scales. The ratios constitute very large, dimensionless numbers: some 40 orders of… … Wikipedia
Dirac equation — Quantum field theory (Feynman diagram) … Wikipedia
Dirac, P.A.M. — ▪ English physicist in full Paul Adrien Maurice Dirac born August 8, 1902, Bristol, Gloucestershire, England died October 20, 1984, Tallahassee, Florida, U.S. English theoretical physicist who was one of the founders of quantum mechanics… … Universalium
Dirac equation in the algebra of physical space — v · Paravector algebra Applications in Physics … Wikipedia
Dirac bracket — The Dirac bracket is a generalization of the Poisson bracket developed by Paul Dirac to correctly treat systems with second class constraints in Hamiltonian mechanics and canonical quantization. It is an important part of Dirac s development of… … Wikipedia
Mass gap — Quantum field theory (Feynman diagram) … Wikipedia
Fermi–Dirac statistics — Statistical mechanics Thermodynamics · … Wikipedia
Paul Dirac — Paul Adrien Maurice Dirac Born Paul Adrien Maurice Dirac 8 August 1902(1902 08 08) Bristol, England … Wikipedia
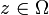 wird sein Diracmaß (auch Punktmaß) δz zugeordnet, indem man festlegt, dass jede Menge
wird sein Diracmaß (auch Punktmaß) δz zugeordnet, indem man festlegt, dass jede Menge 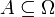 das Maß 1 hat, wenn sie den Punkt z enthält, und das Maß 0, wenn sie ihn nicht enthält:
das Maß 1 hat, wenn sie den Punkt z enthält, und das Maß 0, wenn sie ihn nicht enthält: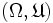 definieren und macht diesen zum Maßraum
definieren und macht diesen zum Maßraum 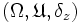 , sogar zu einem Wahrscheinlichkeitsraum, da die Gesamtmasse δz(Ω) = 1 ist. Daraus folgt trivialerweise, dass das Maß endlich ist, insbesondere ist der Maßraum σ-endlich.
, sogar zu einem Wahrscheinlichkeitsraum, da die Gesamtmasse δz(Ω) = 1 ist. Daraus folgt trivialerweise, dass das Maß endlich ist, insbesondere ist der Maßraum σ-endlich.