- Drehmoment
-
Physikalische Größe Name Drehmoment Formelzeichen der Größe 
Größen- und
Einheiten-
systemEinheit Dimension SI N m M·L2·T−2 Das Drehmoment ist eine grundlegende physikalische Größe in der klassischen Mechanik. Es spielt für Drehbewegungen die gleiche Rolle wie die Kraft für die geradlinige Bewegung. Ein Drehmoment kann einen Körper biegen, tordieren oder seine Rotation beschleunigen. Die international verwendete Maßeinheit für das Drehmoment ist das Newtonmeter.
Ein Drehmoment wirkt zum Beispiel auf einen Körper, der sich um einen festgehaltenen Punkt drehen kann, wenn an ihm außerhalb dieses Punktes eine Kraft angreift.[1] Der Betrag des Drehmomentes ist der Betrag der Kraft multipliziert mit dem senkrechten Abstand des Drehpunktes von der Wirkungslinie der Kraft, dem sogenannten Hebelarm.[2]
In mathematischer Beschreibung ist das Drehmoment das Vektorprodukt aus Abstandsvektor und Kraftvektor.
Inhaltsverzeichnis
Unterschiedliche Bezeichnungen in der Technik
In der Technik wird dem Drehmoment je nach Anwendung eine unterschiedliche Bezeichnung gegeben:
- Abtriebsmoment
- Das an der Welle eines Motors wirksame Drehmoment.
- Anfahrmoment
- Das Drehmoment, das ein Motor aus dem Stand leisten kann.
- Antriebsmoment
- Das Drehmoment, das an der Eingangswelle einer Arbeitsmaschine wirkt. Außerdem das an den Radachsen eines Fahrzeugs oder an der Achse eines Propellers wirksame Drehmoment.
- Anziehdrehmoment bzw. Anzugsdrehmoment
- Das Drehmoment, das beim Anziehen einer Schraube durch den Schraubenschlüssel aufgebracht wird.
- Biegemoment
- Das Drehmoment, das für eine elastische Biegung eines Bauteils nötig ist.
- Kippmoment
- Das maximale Drehmoment, das eine Asynchronmaschine aufbringen kann. Bei höherer Belastung „kippt“ diese Maschine, sie bleibt stehen oder „dreht durch“.
- Kräftepaar
- Das Drehmoment durch zwei gleich große Kräfte, die in entgegengesetzter Richtung und zueinander versetzt auf einen Körper einwirken[3].
- Lastmoment
- Das Drehmoment, das eine anzutreibende Arbeitsmaschine dem antreibenden Motor entgegensetzt.
- Bemessungsmoment
- Nennmoment
- Torsionsmoment
- Das Drehmoment, das für eine Verwindung eines Bauteils nötig ist.
Maßeinheit
Die Maßeinheit des Drehmoments ist das Newtonmeter (N m). Mit den Basiseinheiten Kilogramm, Meter und Sekunde gilt:
Die Maßeinheit für die Energie lässt sich mit der gleichen Kombination von Basiseinheiten angeben. Sowohl Drehmoment als auch Energie lassen sich als „Kraft mal Strecke“ auffassen. Dennoch sind Energie und Drehmoment unterschiedliche physikalische Größen, die sich nicht ineinander umrechnen lassen. Energie wird umgewandelt, wenn bei einer Bewegung entlang einer Strecke eine Kraft parallel zur Bewegung wirkt. Beim Drehmoment wirkt dagegen die Kraft senkrecht zu der durch den Hebelarm gebildeten Strecke.
Das Drehmoment als Kreuzprodukt und axialer Vektor
Bei der Beschreibung des Drehmoments als Vektorprodukt aus Kraft- und Abstandsvektor gilt für die Seite, in die der auf beiden Vektoren senkrechte Ergebnisvektor zeigt, die Drei-Finger-Regel. Dieser Vektor kennzeichnet sowohl den Betrag als auch den Drehsinn des Drehmoments, denn das Vektorprodukt zeichnet weniger eine Richtung als einen Drehsinn aus.[4] Der Drehsinn ist mit der Korkenzieherregel codiert.
Das Vektorprodukt für eine am Punkt
 angreifenden Kraft
angreifenden Kraft  lautet für das Drehmoment
lautet für das Drehmoment  in Bezug auf den Punkt
in Bezug auf den Punkt  wie folgt:
wie folgt: .
.
 und
und  sind die Ortsvektoren von Angriffs- beziehungsweise Bezugspunkt.
sind die Ortsvektoren von Angriffs- beziehungsweise Bezugspunkt.Der Kraftpfeil lässt sich auf seiner Wirkungslinie so verschieben, dass der Abstandsvektor
 senkrecht zu ihm steht, wie im Bild rechts. Der Abstandsvektor in dieser Lage wird als Hebelarm bezeichnet. Betragsmäßig gilt dann Kraft mal Hebelarm. Der rote Pfeil stellt das Drehmoment als Vektor
senkrecht zu ihm steht, wie im Bild rechts. Der Abstandsvektor in dieser Lage wird als Hebelarm bezeichnet. Betragsmäßig gilt dann Kraft mal Hebelarm. Der rote Pfeil stellt das Drehmoment als Vektor  dar. Seine Länge ist ein Maß für den Betrag, seine Richtung ein Zeichen für den Drehsinn, wobei die Korkenzieherregel anzuwenden ist. Die Richtung der in Abwesenheit von Gegenmomenten beschleunigten Drehbewegung des Zylinders wird von einem zusätzlich gezeichneten, zum Kreis gebogenen Pfeil angedeutet. Da die Pfeilspitze nicht eine lineare sondern eine Drehrichtung symbolisiert, wird der Drehmomenten-Vektor gelegentlich auch mit einer doppelten Spitze gezeichnet.[5] Der Bezugspunkt
dar. Seine Länge ist ein Maß für den Betrag, seine Richtung ein Zeichen für den Drehsinn, wobei die Korkenzieherregel anzuwenden ist. Die Richtung der in Abwesenheit von Gegenmomenten beschleunigten Drehbewegung des Zylinders wird von einem zusätzlich gezeichneten, zum Kreis gebogenen Pfeil angedeutet. Da die Pfeilspitze nicht eine lineare sondern eine Drehrichtung symbolisiert, wird der Drehmomenten-Vektor gelegentlich auch mit einer doppelten Spitze gezeichnet.[5] Der Bezugspunkt  befindet sich auf der Achse des gezeichneten Zylinders. Er wird mit dem Kreuzprodukt nicht beschrieben.
befindet sich auf der Achse des gezeichneten Zylinders. Er wird mit dem Kreuzprodukt nicht beschrieben.Das Drehmoment hat auch die Eigenschaften, die mit einem axialen Vektor beschrieben werden können.
Ähnlichkeit von Kraft und Drehmoment
Das Drehmoment nimmt in der klassischen Mechanik für Drehbewegungen eine ähnliche Rolle ein, wie die Kraft für geradlinige Bewegungen.
Entsprechungen zwischen geradliniger Bewegung und Drehbewegung|
Geradlinige Bewegung Drehbewegung gegen einen Widerstand geleistete Arbeit Kraft mal Weg

Drehmoment mal Drehwinkel

Leistung (Physik) Kraft mal Geschwindigkeit

Drehmoment mal Winkelgeschwindigkeit

2. Newtonsches Gesetz Kraft gleich Masse mal Beschleunigung

Drehmoment gleich Trägheitsmoment mal Winkelbeschleunigung

Zeitintegral liefert Impuls

Drehimpuls

Messung des Drehmoments
ruhender Körper
Ein auf einen drehbaren, aber ruhenden Körper wirkendes Drehmoment lässt sich durch Anbringen eines statischen Gegenmomentes messen. Direkte Messgröße ist die über einen in der Länge bekannten Hebelarm aufzubringende Gegenkraft, bei der der Körper in Ruhe bleibt. Das zu messende Drehmoment ergibt sich aus dem Produkt der Werte der Gegenkraft und der Hebelarmlänge.
drehender Körper
Das die Drehgeschwindigkeit verändernde Drehmoment lässt sich durch Messen der Winkelbeschleunigung α bestimmen, wenn das Trägheitsmoment J bekannt ist. Die Auswertung erfolgt mit der Formel
 .
.
Bei Übertragung einer Leistung P zum Beispiel über rotierende Welle interessiert die Abhängigkeit des dabei wirkenden Drehmomentes von der Drehzahl n (Drehmomentkurve). Dafür ist der Beharrungszustand n=konstant herzustellen. Gemessen werden die Leistung und die Drehzahl. Die Auswertung erfolgt mit der Formel
 .
.
Das Messen der Leistung erfolgt mit Hilfe einer sogenannten Leistungsbremse: Pendelmaschine, Pronyscher Zaum oder Wasserwirbelbremse.
Drehmomente an ausgewählten Maschinen
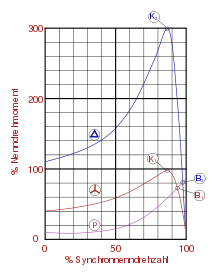 Drehmomentkennlinien eines Asynchronmotors
Drehmomentkennlinien eines Asynchronmotors
obere Kennlinie: Dreieckschaltung
mittlere Kennlinie: SternschaltungBeispiel: Elektromotor
Elektromotoren haben ein relativ hohes Anfahrmoment, das bei Drehstrommotoren durch temporären Betrieb in Dreieckschaltung noch erhöht werden kann. Das Bild zeigt das Abtriebsmoment eines Asynchronmotors in Abhängigkeit von der Drehzahl. Der normale Betriebsbereich ist rechts von den Kipppunkten K1 oder K2 auf der steil abfallenden Kurve. Der Bereich links von den Kipppunkten ist der Anfahrbereich, der wegen des schlechten Wirkungsgrads möglichst schnell durchfahren werden soll.
Beispiel: Drehmoment und Leistung eines Verbrennungsmotors
Der bei Automobilen verwendete Begriff maximales Drehmoment des Verbrennungsmotors bei einer bestimmten Drehzahl bezeichnet das maximale vom Motor an der Kurbelwelle abgegebene Drehmoment. Das an der Kurbelwelle bei Volllast abgegebene Drehmoment ist nicht über den gesamten Drehzahlbereich des Motors konstant, sondern hat in einem bestimmten Bereich des nutzbaren Drehzahlbereiches ein Maximum.
Das Drehmoment M für Viertaktmotoren berechnet sich aus:
Hierbei ist Vh das Hubvolumen und pe der effektive Mitteldruck, der Faktor 2π im Nenner stammt aus der Formel für die Arbeit eines Drehmoments, die entlang des Umfanges 2π verrichtet wird. Der Wert 2π wird bei Viertaktmotoren mit 2 multipliziert, da Viertaktmotoren nur bei jeder zweiten Umdrehung Arbeit verrichten. Für Zweitaktmotoren gilt entsprechend:
Rechenbeispiel für das Drehmoment eines Serienfahrzeuges mit 2000 cm³ (=0,002 m³) Hubvolumen, dessen Viertaktmotor bei einer Drehzahl von 2000/min einen Mitteldruck von 22 Bar (=2.200.000 Pa; 1 Pa = 1 N/m²) erreicht, in SI-Einheiten gerechnet:
Die Gleichung für die Leistung bei einer Drehbewegung lautet (siehe oben):
und für eine drehzahlabhängige Leistung

- M(n) ist die für die untersuchte Maschine typische drehzahlabhängige Drehmomentkenngröße, die durch Messung erhalten wird.
Bei einem Verbrennungsmotor, der bei 2000 Umdrehungen pro Minute ein Drehmoment von 350 N m abgibt, berechnet sich die Leistung wie folgt:
Häufig wird bei Leistungsberechnungen dieser Art die Zahlenwertgleichung benutzt.
Beispiel: Leistung und Drehmoment eines Hydraulikmotors
Die hydraulische Leistung P eines Hydraulikmotors errechnet sich aus den Drücken p1 und p2 am Motoreingang bzw. -ausgang und dem geschlucktem Ölvolumen Q = q · n (q = Volumen je Umdrehung):
Aus der Gleichung für die Leistung bei einer Drehbewegung (siehe oben)
folgt das Drehmoment mit:
Einzelnachweise
- ↑ Alfred Recknagel: Physik - Mechanik, Verlag Technik, Berlin, 1955, S.181
- ↑ Alfred Recknagel: Physik - Mechanik, Verlag Technik, Berlin, 1955, S.182
- ↑ Alfred Recknagel: Physik - Mechanik, Verlag Technik, Berlin, 1955, S.176
- ↑ Wolfgang Nolting: Grundkurs Theoretische Physik 1, Springer 2011, ISBN 978-3-642-12947-6, Seite 63
- ↑ Unterscheidung des Momentenvektors vom Kraftvektor durch eine doppelte Pfeilspitze [1]
Literatur
- Wolfgang Nolting: Klassische Mechanik. In: Grundkurs Theoretische Physik. Bd. 1, 8. Auflage. Springer, Berlin 2008, ISBN 978-3-540-34832-0.
- Herbert Goldstein, Charles P. Poole und John L. Safko: Klassische Mechanik (Übersetzung: Michael Baer). - 3., vollst. überarb. und erw. Aufl - Weinheim : Wiley-VCH, 2006. (Lehrbuch Physik) - ISBN 3-527-40589-5
- Richard P. Feynman: Feynman-Vorlesungen über Physik. Oldenbourg, München/Wien 2007, ISBN 978-3-486-58444-8.
- Paul A. Tipler: Physik. 3. korrigierter Nachdruck der 1. Auflage. 1994, Spektrum Akademischer Verlag, Heidelberg/Berlin, 2000, ISBN 3-86025-122-8.
- Ludwig Bergmann, Clemens Schaefer: Mechanik - Akustik - Wärme. In: Lehrbuch der Experimentalphysik. Bd. 1, 12. Auflage. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-019311-4.
- Istvan Szabó: Einführung in die Technische Mechanik, Springer, 1999, ISBN 3-540-44248-0
- Peter Gummert, Karl-August Reckling: Mechanik, Vieweg, 1994, ISBN 3-528-28904-X
Weblinks
 Commons: Drehmoment – Sammlung von Bildern, Videos und AudiodateienKategorie:
Commons: Drehmoment – Sammlung von Bildern, Videos und AudiodateienKategorie:- Physikalische Größenart
Wikimedia Foundation.










