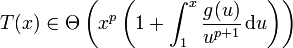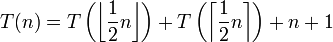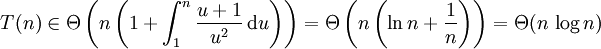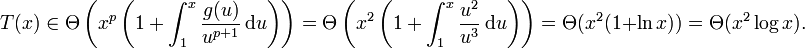- Akra-Bazzi-Methode
-
In der Informatik dient das Akra-Bazzi-Theorem, oder auch die Akra-Bazzi-Methode, dazu, das asymptotische Verhalten von Lösungen mathematischer Rekursionsgleichungen zu bestimmen, die bei der asymtotischen Analyse insbesondere von Divide-and-Conquer-Algorithmen auftreten. Es wurde 1998 veröffentlicht und ist eine Verallgemeinerung des Master-Theorems, das nur auf diejenigen Divide-and-Conquer-Algorithmen angewandt werden kann, deren Teilprobleme gleiche Größe haben.
Inhaltsverzeichnis
Mathematische Formulierung
Gegeben sei die Rekursionsgleichung
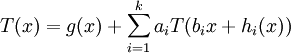 für
für 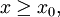
für eine Funktion
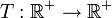 , so dass die folgenden Bedingungen erfüllt sind:
, so dass die folgenden Bedingungen erfüllt sind:- Es sind genügend Basisfälle vorhanden, so dass die Gleichung eindeutig lösbar ist;
- ai und bi sind für alle i konstant, mit ai > 0 und 0 < bi < 1;
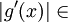 O(xc), wobei c eine Konstante ist;
O(xc), wobei c eine Konstante ist;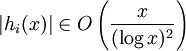 für alle i;
für alle i;- x0 ist eine Konstante.
Dann gilt für das asymptotische Verhalten von T(x) die Abschätzung in der Theta-Notation
mit
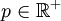 , so dass
, so dass 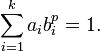
Intuitiv ist hi(x) eine kleine Störung des Arguments von T. Wegen
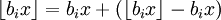 und da
und da 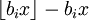 stets zwischen 0 und 1 ist, kann hi(x) dazu benutzt werden, die Gauß-Klammer ("Floor-Funktion") im Argument zu ignorieren. Ähnlich kann man für die Irrelevanz der Aufrundungsfunktion ("Ceiling-Funktion") für das asymptotische Verhalten von T argumentieren. Beispielsweise haben
stets zwischen 0 und 1 ist, kann hi(x) dazu benutzt werden, die Gauß-Klammer ("Floor-Funktion") im Argument zu ignorieren. Ähnlich kann man für die Irrelevanz der Aufrundungsfunktion ("Ceiling-Funktion") für das asymptotische Verhalten von T argumentieren. Beispielsweise haben 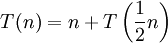 und
und 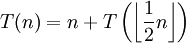 gemäß dem Akra-Bazzi-Theorem dasselbe asymptotische Verhalten.
gemäß dem Akra-Bazzi-Theorem dasselbe asymptotische Verhalten.Beispiele
Mergesort
Für den Mergesort ist die erforderliche Anzahl T(n) von Vergleichen, die näherungsweise proportional zu dessen Laufzeit ist, gegeben durch die Rekursionsgleichung
mit dem Basisfall T(1) = 0. Somit lässt sich das Akra-Bazzi-Theorem anwenden, welches mit g(u) = u + 1 und k=2, a1 = a2 = 1, b1 = b2 = 1 / 2, zunächst p=1 und damit das asymptotische Verhalten
ergibt.
Divide-and-Conquer mit ungleichen Teilproblemen
Sei T(n) definiert als 1 für
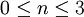 und
und 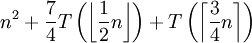 für n > 3. Gemäß der Akra-Bazzi-Methode wird im ersten Schritt der Wert von p berechnet, so dass
für n > 3. Gemäß der Akra-Bazzi-Methode wird im ersten Schritt der Wert von p berechnet, so dass 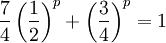 . Das ergibt hier p = 2. Im zweiten Schritt wird das asymptotische Verhalten nach der Formel berechnet:
. Das ergibt hier p = 2. Im zweiten Schritt wird das asymptotische Verhalten nach der Formel berechnet:Bedeutung
Das Akra-Bazzi-Theorem umfasst eine sehr weite Klasse von Rekursionsgleichungen und verallgemeinert wesentlich zuvor bekannte Sätze zur Bestimmung von asymptotischem Verhalten. Vorwiegend wird es für die Komplexitätsbetrachtung rekursiver Algorithmen verwendet, insbesondere von Divide-and-Conquer-Algorithmen.
Quellen
- Mohamad Akra, Louay Bazzi: On the solution of linear recurrence equations. Computational Optimization and Applications 10(2), 1998, pp. 195-210.
- Tom Leighton: Notes on Better Master Theorems for Divide-and-Conquer Recurrences, Manuscript. Massachusetts Institute of Technology, 1996.
Wikimedia Foundation.