- FLD
-
Die Fisher’sche Diskriminanzfunktion ist eine Diskriminanzfunktion, die das Fisher’sche Kriterium realisiert. Dieses wurde 1936 von R. A. Fisher entwickelt und beschreibt eine Metrik, die die Güte der Trennbarkeit zweier Klassen in einem Merkmalsraum misst.
Die Fisher’sche Diskriminanzfunktion wurde 1936 von R. A. Fisher in The use of multiple measurements in taxonomic problems veröffentlicht.
Inhaltsverzeichnis
Grundlegendes
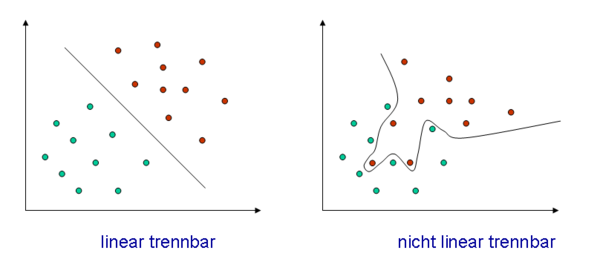
Gegeben seien N d-dimensionale Merkmalsvektoren x, von denen n1 der Klasse C1 und n2 der Klasse C2 angehören. Eine Diskriminanzfunktion beschreibt nun die Gleichung einer Hyperebene, die die Klassen optimal voneinander trennt. Davon gibt es, je nach Trennbarkeit der Klassen, lineare und nicht-lineare, was im folgenden Bild in zwei Dimensionen erläutert ist.
Fisher’sches Kriterium
Das Berechnen der optimal trennenden Hyperebene ist in zwei Dimensionen noch relativ einfach, wird jedoch in mehreren Dimensionen schnell zu einem komplexeren Problem. Daher bedient sich Fisher eines Tricks, der zunächst die Dimension reduziert und danach die Diskriminanzfunktion berechnet. Dazu werden die Daten in eine einzige Dimension projiziert, wobei die Projektionsrichtung von entscheidender Bedeutung ist.
Die Klassen sind viel besser voneinander getrennt, wenn die Merkmalsvektoren in Richtung w2 projiziert sind, als in Richtung w1.
Um diese Tatsache formal zu schreiben, werden ein paar Definitionen benötigt.
Bezeichne
 den Mittelwert der Klasse Ci und
den Mittelwert der Klasse Ci und 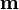 den Mittelwert des gesamten Merkmalsraumes.
den Mittelwert des gesamten Merkmalsraumes.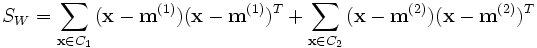
heißt Intravarianz (englisch: within scatter) und misst die Varianz innerhalb der Klassen, während die Intervarianz (englisch: between scatter)
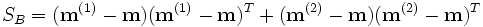
die Varianz zwischen den Klassen beschreibt. Die geeignetste Projektionsrichtung ist dann offensichtlich diejenige, die die Intravarianz der einzelnen Klassen minimiert, während die Intervarianz zwischen den Klassen maximiert wird.
Diese Idee wird mit dem Fisher’schen Kriterium anhand des Rayleigh-Koeffizienten mathematisch formuliert:
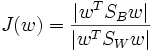
Mit diesem Kriterium wird die Güte der Trennbarkeit der Klassen im Merkmalsraum gemessen. Damit gilt dann, dass die Projektionsrichtung w genau dann optimal ist (im Sinne der Trennbarkeit der Klassen), wenn J(w) maximal ist.
Die Erläuterungen lassen bereits erkennen, dass das Fisher'sche Kriterium nicht nur zu einer Diskriminanzfunktion, sondern auch zu einem Optimierungsverfahren für Merkmalsräume erweitert werden kann. Bei letzterem wäre ein Projektionsverfahren denkbar, das einen hochdimensionalen Merkmalsraum ähnlich der Hauptkomponentenanalyse in eine niedere Dimension projiziert und dabei gleichzeitig die Klassen optimal voneinander trennt.
Fisher’sche Diskriminanzfunktion
Eine Diskriminanzfunktion ordnet Objekte den jeweiligen Klassen zu. Mit dem Fisher’schen Kriterium kann bereits die optimale Projektionsrichtung, genauer gesagt der Normalenvektor der optimal trennenden Hyperebene, bestimmt werden. Es muss dann nur noch für jedes Objekt getestet werden, auf welcher Seite der Hyperebene es liegt.
Dazu wird das jeweilige Objekt zunächst auf die optimale Projektionsrichtung projiziert. Danach wird der Abstand zum Ursprung gegen einen vorher bestimmten Schwellwert w0 getestet. Die Fisher’sche Diskriminanzfunktion ist demnach von folgender Form:

Ein neues Objekt y wird nun je nach Ergebnis von f(y) entweder C1 oder C2 zugewiesen. Bei f(y) = 0 ist anwendungsabhängig zu entscheiden, ob y überhaupt einer der beiden Klassen zuzuordnen ist.
Literatur
- Christopher M. Bishop, Neural Networks for Pattern Recognition, Oxford University Press, 1995.
- Richard O. Duda and Peter E. Hart, Pattern Classification and Scene Analysis, Wiley-Interscience Publication, 1974.
- Keinosuke Fukunaga, Introduction to Statistical Pattern Recognition, Academic Press, 1990.
Wikimedia Foundation.