- Fast überall
-
Die Maßtheorie ist ein Teilgebiet der Mathematik, das die elementargeometrischen Begriffe Streckenlänge, Flächeninhalt, Volumen verallgemeinert und es dadurch ermöglicht, auch komplizierteren Mengen ein Maß zuzuordnen. Sie bildet das Fundament der modernen Integrations- und Wahrscheinlichkeitstheorie.
Als Maß versteht man in der Maßtheorie eine Zuordnung von reellen oder komplexen Zahlen zu einem Teilmengensystem über einer Grundmenge. Die Zuordnung und das Teilmengensystem sollen dabei bestimmte Eigenschaften besitzen. In der Praxis ist häufig nur eine partielle Zuordnung von vornherein bekannt. Zum Beispiel ordnet man in der Ebene Rechtecken das Produkt ihrer Kantenlängen als Flächeninhalt zu. Die Maßtheorie untersucht nun einerseits, ob sich in konsistenter Weise und eindeutig diese Zuordnung auf größere Teilmengensysteme erweitern lässt, und andererseits, ob dabei zusätzliche gewünschte Eigenschaften erhalten bleiben. Im Beispiel der Ebene möchte man natürlich auch Kreisscheiben einen sinnvollen Flächeninhalt zuordnen und wird gleichzeitig neben den Eigenschaften, die man von Maßen ganz allgemein verlangt, auch Translationsinvarianz fordern, das heißt, der Inhalt einer Teilmenge der Ebene ist unabhängig von ihrer Position.
Inhaltsverzeichnis
Motivation
Der komplizierte Aufbau der Maßtheorie wird dadurch verursacht, dass es nicht möglich ist, eine Maßfunktion zu finden, die beliebigen Teilmengen der reellen Zahlen (bzw. des n-dimensionalen reellen Raumes) ein sinnvolles Maß zuordnet, das zum Beispiel in der reellen Ebene dem klassischen Flächeninhalt oder im dreidimensionalen reellen Raum dem klassischen Volumen entspricht. Was dabei sinnvoll genau bedeutet, wurde erstmals im sogenannten Maßproblem von Henri Lebesgue in seiner Pariser Thèse 1902 beschrieben und entspricht im Fall der reellen Ebene mit dem Flächeninhalt als Maßfunktion den folgenden Forderungen:
- ein Quadrat mit der Kantenlänge eins hat den Flächeninhalt eins („Normiertheit“)
- die Verschiebung einer beliebigen Fläche ändert nicht ihren Flächeninhalt („Bewegungsinvarianz“)
- endliche und abzählbare Vereinigungen von disjunkten Flächen haben den gleichen Flächeninhalt wie die Summe aller Teilflächen („σ-Additivität“)
1905 konnte Giuseppe Vitali zeigen, dass dieses Problem für beliebige Teilmengen nicht lösbar ist. Schränkt man jedoch die zu messenden Mengen ein und betrachtet nur ein bestimmtes Mengensystem, so kann man das Maßproblem lösen und auf diesem Mengensystem ein Maß mit den gewünschten Eigenschaften definieren (siehe Definition Maß weiter unten).
Einen anderen Weg wählte Felix Hausdorff, der das Inhaltsproblem formulierte, indem er die dritte Forderung abschwächte und sich auf endliche Vereinigungen beschränkte. Er konnte 1914 zeigen, dass dieses im Allgemeinen (Dimension
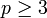 ) auch nicht lösbar ist. Ausnahmen bilden die reellen Zahlen und die reelle Ebene, für die es eine sogenannte Inhaltsfunktion gibt (siehe Definition Inhalt weiter unten).
) auch nicht lösbar ist. Ausnahmen bilden die reellen Zahlen und die reelle Ebene, für die es eine sogenannte Inhaltsfunktion gibt (siehe Definition Inhalt weiter unten).Die Maßtheorie beschäftigt sich also mit verschiedenen Mengensystemen und den Inhaltsfunktionen, die man darauf definieren kann. Dabei werden nicht nur reelle Mengensysteme betrachtet, sondern abstrakte Mengensysteme erzeugt durch beliebige Grundmengen; womit sich, bei geringem Mehraufwand, die Ergebnisse besser in Funktionalanalysis und Wahrscheinlichkeitstheorie anwenden lassen.[1]
Definitionen und Beispiele
Die zu messenden Mengen fasst man in Mengensysteme zusammen, die unterschiedlich stark gegenüber Mengenoperationen abgeschlossen sind. Bedeutende Beispiele für Mengensysteme sind:
Halbring (Mengensystem), σ-Algebra, Potenzmenge
Dabei ist die Potenzmenge das umfassendste aller Mengensysteme und enthält jede beliebige Teilmenge der Grundmenge. Am eingeschränktesten ist der Halbring, der die Grundlage des Lebesgue-Maßes bildet und nur ganz bestimmte Teilmengen enthält. Weit weniger eingeschränkt ist die σ-Algebra, die das wichtigste Mengensystem der Maßtheorie ist. Es gilt: Jede Potenzmenge ist eine σ-Algebra und jede σ-Algebra ist ein Halbring. Weitere in der Maßtheorie benutzte Mengensysteme sind:
Ring (Mengensystem), Algebra (Mengensystem) oder Dynkin-System
Auf diesen Mengensystemen definiert man die Inhaltsfunktionen wie Inhalt, Prämaß, Maß oder Äußeres Maß.
Es folgen einige Definitionen der Grundbegriffe der Maßtheorie.
Inhalt
Ein Inhalt μ ist eine Funktion, die jeder Menge S aus einem Halbring
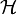 über Ω einen Wert μ(S) zuordnet. Dieser Wert ist entweder eine nichtnegative reelle Zahl oder
über Ω einen Wert μ(S) zuordnet. Dieser Wert ist entweder eine nichtnegative reelle Zahl oder  .
.Für diese Abbildung
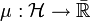 muss also gelten:
muss also gelten:- Die leere Menge hat den Inhalt null:
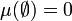 .
. - Der Inhalt ist endlich additiv. Sind also
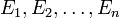 endlich viele paarweise disjunkte Mengen aus
endlich viele paarweise disjunkte Mengen aus 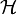 und ist E deren Vereinigungsmenge, dann gilt für den Inhalt μ(E)
und ist E deren Vereinigungsmenge, dann gilt für den Inhalt μ(E)
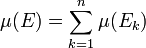 .
.
Eigenschaften
- Monotonie: Sind E1 und E2 Mengen aus
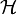 mit
mit  , so gilt
, so gilt 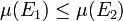 .
. - Fortsetzbarkeit: Man kann zu jeden Inhalt μ auf
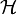 einen Inhalt μ' auf dem von
einen Inhalt μ' auf dem von 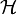 erzeugten Ring
erzeugten Ring 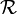 konstruieren, indem man μ' definiert durch:
konstruieren, indem man μ' definiert durch:
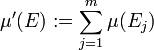
- Aufgrund der Eigenschaften eines Halbringes gibt es für alle
 Mengen
Mengen  mit
mit 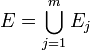 .
.
- Dann gilt für einen Inhalt
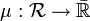 auf dem Ring
auf dem Ring 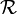 :
:
- Subtraktivität: für
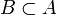 mit
mit 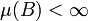 gilt
gilt 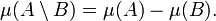
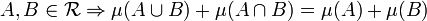
- Subadditivität:
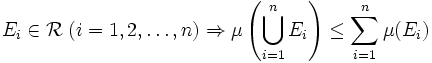
- σ-Superadditivität: Seien
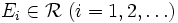 paarweise disjunkt mit
paarweise disjunkt mit 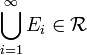 . Dann folgt aus der Additivität und Monotonie
. Dann folgt aus der Additivität und Monotonie 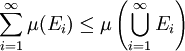
- Subtraktivität: für
Nullmenge
→ Hauptartikel: Nullmenge
Eine Menge A aus
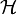 heißt Nullmenge, wenn μ(A) = 0 gilt.
heißt Nullmenge, wenn μ(A) = 0 gilt.Prämaß
Ein σ-additiver (bzw. abzählbar additiver) Inhalt heißt Prämaß. Sei
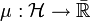 ein Inhalt, dann ist μ ein Prämaß, wenn für jede Folge
ein Inhalt, dann ist μ ein Prämaß, wenn für jede Folge 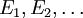 abzählbar vieler paarweise disjunkter Mengen aus
abzählbar vieler paarweise disjunkter Mengen aus 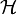 mit
mit 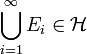 gilt:
gilt:Eigenschaften
- Fortsetzbarkeit: Man kann auch zu jeden Prämaß μ auf
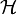 ein Prämaß μ' auf dem von
ein Prämaß μ' auf dem von 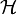 erzeugten Ring
erzeugten Ring 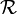 konstruieren, indem man μ' definiert durch:
konstruieren, indem man μ' definiert durch:
- Dann gilt für das Prämaß
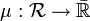 auf dem Ring
auf dem Ring 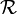 :
:
- Stetigkeit von oben: Ist
 eine absteigende Folge von Mengen aus Σ mit
eine absteigende Folge von Mengen aus Σ mit 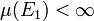 und ist E deren Durchschnitt, so ist
und ist E deren Durchschnitt, so ist 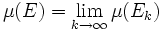 .
. - Stetigkeit von unten: Ist
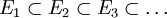 eine aufsteigende Folge von Mengen aus Σ und ist E deren Vereinigungsmenge, so ist
eine aufsteigende Folge von Mengen aus Σ und ist E deren Vereinigungsmenge, so ist 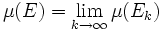 .
.
- Stetigkeit von oben: Ist
Maß
Ein Maß μ ist eine Funktion, die jeder Menge S aus der σ-Algebra Σ in Ω einen Wert μ(S) zuordnet. Dieser Wert ist entweder eine nichtnegative reelle Zahl oder
 (siehe unten wegen möglicher Verallgemeinerungen). Ferner muss gelten:
(siehe unten wegen möglicher Verallgemeinerungen). Ferner muss gelten:- Die leere Menge hat das Maß null:
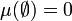 .
. - Das Maß ist abzählbar additiv (auch σ-additiv). Sind also E1, E2, E3, ... abzählbar viele paarweise disjunkte Mengen aus Σ und ist E deren Vereinigungsmenge, dann gilt für das Maß μ(E):
 .
.- Damit ist das Maß auch endlich additiv, indem man die Folge
 paarweise disjunkter Mengen aus Σ wählt.
paarweise disjunkter Mengen aus Σ wählt.
Somit ist jedes Maß auch ein Inhalt bzw. Prämaß und besitzt alle Eigenschaften, die dort aufgezählt wurden.
Eigenschaften
- endlich: Ein Maß μ heißt endlich, wenn gilt
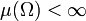 . Aufgrund der Monotonie ist dies gleichbedeutend damit, dass für alle
. Aufgrund der Monotonie ist dies gleichbedeutend damit, dass für alle 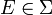 gilt
gilt 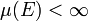 .
. - σ-endlich: Ein Maß heißt σ-endlich (bzw. σ-finit), wenn es eine abzählbare Folge messbarer Mengen
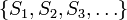 gibt, die alle ein endliches Maß
gibt, die alle ein endliches Maß 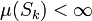 besitzen und Ω überdecken. σ-endliche Maße haben einige schöne Eigenschaften, die gewisse Analogien zu den Eigenschaften separabler topologischer Räume aufweisen.
besitzen und Ω überdecken. σ-endliche Maße haben einige schöne Eigenschaften, die gewisse Analogien zu den Eigenschaften separabler topologischer Räume aufweisen. - vollständig: Ein Maß heißt vollständig genau dann, wenn jede Teilmenge jeder Nullmenge in Σ enthalten ist.
Messraum, messbare Mengen
Sei Σ eine σ-Algebra aus Teilmengen von Ω. Dann nennt man das Paar (Ω, Σ) Messraum oder messbarer Raum.
Eine Funktion, die die Struktur eines Messraums erhält, heißt messbare Funktion.
Jedes Element S von Σ heißt messbar, da die charakteristische Funktion χS messbar ist. Dabei ist zu beachten, dass man in der Maßtheorie zum einen von der Messbarkeit bezüglich eines Messraumes und zum anderen von der Messbarkeit nach Carathéodory bezüglich eines äußeren Maßes spricht. Letztere kann man aber äquivalent als Messbarkeit bezüglich des durch das äußere Maß induzierten Messraumes betrachten.
Beispiele für Messräume:
- Jede Menge bildet mit ihrer Potenzmenge einen Messraum.
- Sei A eine Teilmenge von Ω. Dann ist
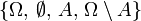 die von A erzeugte σ-Algebra. Diese σ-Algebra ist zugleich die kleinstmögliche σ-Algebra, die A enthält.
die von A erzeugte σ-Algebra. Diese σ-Algebra ist zugleich die kleinstmögliche σ-Algebra, die A enthält.
Maßraum
Eine Struktur (Ω, Σ, μ) heißt Maßraum, wenn (Ω, Σ) ein Messraum und μ ein auf diesem Messraum definiertes Maß ist. Ein Beispiel für einen Maßraum ist der Wahrscheinlichkeitsraum (Ω,Σ,P) aus der Wahrscheinlichkeitstheorie. Er besteht aus der Ergebnismenge Ω, der Ereignisalgebra Σ und dem Wahrscheinlichkeitsmaß P.
fast überall
Eine Eigenschaft gilt fast überall (bzw. μ-fast überall oder μ-fast alle) in (Ω,Σ,μ), wenn es eine Nullmenge gibt, sodass alle Elemente im Komplement die Eigenschaft haben.
Also Eigenschaft E gilt fast überall in
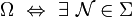 , mit
, mit  und E gilt
und E gilt 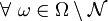 .
.Beachte, dass die Menge, wo sie nicht gilt, nicht unbedingt messbar ist. In der Stochastik wird auf dem Wahrscheinlichkeitsraum (Ω,Σ,P), die Eigenschaft fast überall auch als fast sichere (bzw. P-fast sichere) Eigenschaft bezeichnet.
Vervollständigung
Es sei N das System aller Teilmengen von Mengen
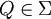 , mit μ(Q) = 0, also aller Mengen, die von Nullmengen überdeckt werden. Ein Maßraum heißt vollständig, falls er alle Mengen in N enthält.
, mit μ(Q) = 0, also aller Mengen, die von Nullmengen überdeckt werden. Ein Maßraum heißt vollständig, falls er alle Mengen in N enthält.Das Tripel (Ω,Σ',μ') nennt man Vervollständigung von (Ω,Σ,μ), man setzt:
 (wobei Δ die symmetrische Differenz ist), und man setzt μ'(aΔn): = μ(a).
(wobei Δ die symmetrische Differenz ist), und man setzt μ'(aΔn): = μ(a).Diese Definition ist sinnvoll, denn wenn aΔn = a'Δn' (mit
 , dann ist
, dann ist 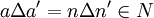 , somit μ(a) = μ(a').
, somit μ(a) = μ(a').Es ist
 und Σ' ist vollständig; daher der Name Vervollständigung.
und Σ' ist vollständig; daher der Name Vervollständigung.Äquivalente Definition
Eine äquivalente Definition der Vervollständigung ist:
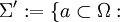 Es existieren
Es existieren 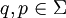 mit
mit  und
und 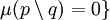 .
.
Beispiele
- Das Nullmaß, das jeder Menge S den Wert μ(S)=0 zuordnet.
- Ein Beispiel für einen Inhalt ist der Jordaninhalt, mit dessen Hilfe man das mehrdimensionale Riemann-Integral definieren kann.
- Das Zählmaß ordnet jeder Teilmenge S einer endlichen oder abzählbar unendlichen Menge die Anzahl ihrer Elemente zu, μ(S)=|S|.
- Das Lebesgue-Maß auf der Menge der reellen Zahlen
 mit der Borelschen σ-Algebra, definiert als translationsinvariantes Maß mit μ([0,1])=1.
mit der Borelschen σ-Algebra, definiert als translationsinvariantes Maß mit μ([0,1])=1. - Das Haar-Maß auf lokal kompakten topologischen Gruppen.
- Ein Wahrscheinlichkeitsmaß oder normiertes Maß ist ein Maß mit μ(Ω)=1.
- Das Zählmaß auf der Menge
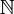 der natürlichen Zahlen ist unendlich, aber σ-endlich.
der natürlichen Zahlen ist unendlich, aber σ-endlich. - Das kanonische Lebesgue-Maß auf der Menge
 der reellen Zahlen ist ebenfalls unendlich, aber σ-endlich, denn
der reellen Zahlen ist ebenfalls unendlich, aber σ-endlich, denn  kann als Vereinigung abzählbar vieler endlicher Intervalle
kann als Vereinigung abzählbar vieler endlicher Intervalle ![\left[ k, k+1\right]](/pictures/dewiki/49/13ab7569fbc5fcef885920b46ffa939f.png) dargestellt werden.
dargestellt werden. - Das Lévy-Maß ist ein zufälliges Maß (random measure) und wird unter anderem benötigt, um Lévy-Prozesse zu charakterisieren. Es gibt die erwartete Anzahl an Sprüngen des Prozesses dieser Höhe im Einheitsintervall an.
Verallgemeinerungen
Eine mögliche Verallgemeinerung betrifft den Wertebereich der Funktion μ.
- Man kann negative reelle oder komplexe Werte zulassen (komplexes oder signiertes Maß).
- Ein weiteres Beispiel einer Verallgemeinerung ist das Spektralmaß, dessen Werte lineare Operatoren sind. Dieses Maß wird insbesondere in der Funktionalanalysis für den Spektralsatz benutzt.
- Allgemein lassen sich Banachraum-wertige Maße betrachten. Siehe Vektorielles Maß. Die beiden letztgenannten sind ebensolche.
Eine andere Möglichkeit der Verallgemeinerung ist die Definition eines Maßes auf der Potenzmenge.
- Siehe äußeres Maß
Historisch wurden zuerst endlich additive Maße eingeführt, die heute auch als Inhalte bezeichnet werden. Die moderne Definition, derzufolge ein Maß abzählbar additiv ist, erwies sich jedoch als nützlicher.
Ergebnisse
Der Satz von Hadwiger klassifiziert alle möglichen translationsinvarianten Maße im
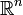 : das Lebesgue-Maß ist ebenso ein Spezialfall wie die Euler-Charakteristik. Verbindungen ergeben sich ferner zu den Minkowski-Funktionalen und den Quermaßen.
: das Lebesgue-Maß ist ebenso ein Spezialfall wie die Euler-Charakteristik. Verbindungen ergeben sich ferner zu den Minkowski-Funktionalen und den Quermaßen.Literatur
- Jürgen Elstrodt: Maß- und Integrationstheorie. 4. Auflage, Springer, Berlin 2005, ISBN 3-540-21390-2.
- Heinz Bauer: Maß- und Integrationstheorie. 2. Auflage, De Gruyter, Berlin 1992, ISBN 3-11-013626-0 (Gebunden), ISBN 3-11-013625-2 (Broschiert).
Einzelnachweise
- ↑ Jürgen Elstrodt: Maß- und Integrationstheorie. S. 3-6 4. Auflage, Springer, Berlin 2005
Siehe auch
Wikimedia Foundation.


