- Fourier-Koeffizienten
-
Dieser Artikel gibt eine Übersicht über die üblichen Varianten der Fourier-Transformation. Häufig wird die kontinuierliche Fourier-Transformation kurz als Fourier-Transformation bezeichnet; für anschauliche Beispiele siehe Artikel Fourier-Analyse und Diskrete Fourier-Transformation. 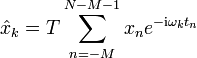 und
und 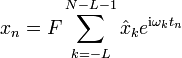 .
.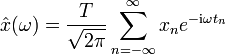 und
und 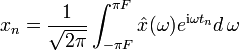 .
.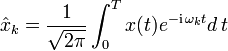 und
und 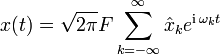 .
.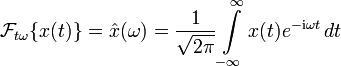
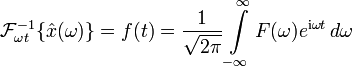
 .
.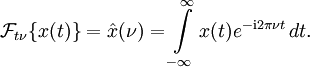
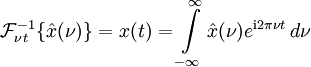 .
.- Dann ist
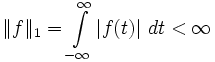 .
. - Für Linearkombinationen gilt
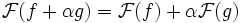 ,
, - Für das Faltungsprodukt gilt
 , bei
, bei 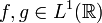 .
. - Sind f und g sogar quadratintegrabel,
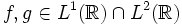 , so gilt die Plancherel-Identität
, so gilt die Plancherel-Identität  .
. - Eine in einem endlichen Intervall periodische Funktion kann in eine Fourier-Reihe zerlegt werden.
- Ein Vorgang, der unperiodisch bis ins Unendliche reicht, erfordert die kontinuierliche Fourier-Transformation (auch Fourier-Integral).
- Sind von einem (unperiodischen) Vorgang nur Werte an diskreten, äquidistanten Zeitpunkten in einem endlichen Intervall bekannt, wird die Diskrete Fourier-Transformation angewendet. Ein Beispiel für einen solchen Vorgang ist ein Musikstück, von welchem zur Speicherung auf einer herkömmlichen Audio-CD pro Sekunde 44100 Amplitudenwerte des Audiosignals am Ausgang eines Mikrophons abgetastet werden.
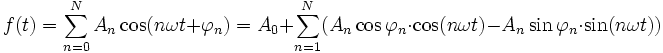
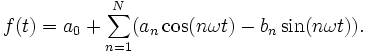
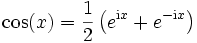 und
und 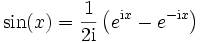 ,
,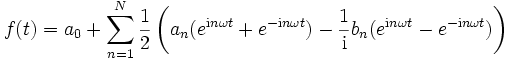
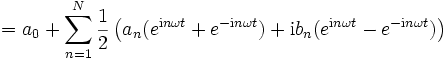
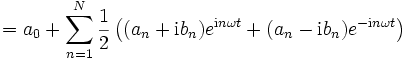
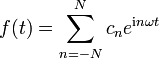
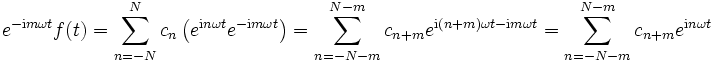
- bei n = 0:
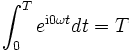
- bei
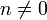 :
: ![\int_0^T e^{\mathrm{i} n \omega t } dt = \left[ \frac1{\mathrm{i}n \omega } e^{\mathrm{i} n\omega t} \right]_0^T](/pictures/dewiki/97/a9e211da030379285f385fbf1aef72f2.png)
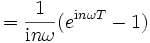
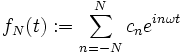
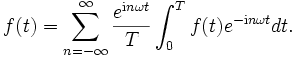
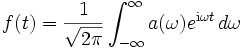
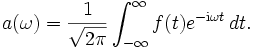
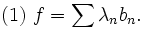

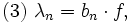
 ,
,- S. Bochner, K. Chandrasekharan: Fourier Transforms. Princeton Book Comp. Publ., 2001, ISBN 0-691-09578-7.
- O. Föllinger, M. Kluwe: Laplace-, Fourier- und z-Transformation. Hüthig, 2003, ISBN 3-7785-2911-0.
- B. Lenze: Einführung in die Fourier-Analysis. Logos Verlag, Berlin 2000, ISBN 3-931216-46-2.
- M. J. Lighthill: Introduction to Fourier Analysis and Generalised Functions. Cambridge University Press, Cambridge 2003, ISBN 0-521-09128-4.
- A. Papoulis: The Fourier Integral and Its Applications. McGraw-Hill, New York 1962, ISBN 0-07-048447-3.
- E. M. Stein, R. Shakarchi: Fourier Analysis: An Introduction. Princeton University Press, Princeton 2003, ISBN 0-691-11384-X.
- Grundlagen der Fourier-Transformation
- Vorlesungsskript Anwendungen der Fourier-Transformation, Teile 1-6.
- Faltung
- Gabor-Transformation
- Diskrete Fourier-Transformation
- Diskrete Kosinustransformation
- Wavelet-Transformation
- Harmonische Analyse
Die Fourier-Transformation ist eine Integraltransformation, die einer gegebenen Funktion eine andere Funktion (ihre Fourier-Transformierte) zuordnet. Sie ist eng mit der Laplace-Transformation verbunden. In vielen Einsatzgebieten wird sie dazu verwendet, um für zeitliche Signale (z. B. ein Sprachsignal oder einen Spannungsverlauf) das Frequenzspektrum zu berechnen (vgl. Fourier-Analyse).
Allgemein umfasst der Begriff Fourier-Transformation eine Reihe sehr ähnlicher Transformationen, welche Funktionen (auch endliche und unendliche Folgen sind Funktionen) in Frequenzkomponenten oder Elementarschwingungen zerlegen. Auf diese wird weiter unten eingegangen.
Die Fourier-Transformation und ihre Varianten sind in vielen Wissenschafts– und Technikzweigen von außerordentlicher praktischer Bedeutung. Die Anwendungen reichen von der Physik (Akustik, Optik, Gezeiten, Astrophysik) über viele Teilgebiete der Mathematik (Zahlentheorie, Statistik, Kombinatorik und Wahrscheinlichkeitstheorie), die Signalverarbeitung und Kryptographie bis zu Ozeanographie und Wirtschaftswissenschaften. Je nach Anwendungszweig erfährt die Zerlegung vielerlei Interpretationen. In der Akustik ist sie beispielsweise die Frequenz-Transformation des Schalls in Oberschwingungen.
Die Fourier-Transformation wurde von dem französischen Mathematiker Jean Baptiste Joseph Fourier im Jahr 1822 in seiner Théorie analytique de la chaleur entwickelt.
Inhaltsverzeichnis |
Varianten der Fourier-Transformation
Die verschiedenen Varianten der Fourier-Transformation sind in folgender Tabelle zusammengefasst. Dabei sind die Formeln als formal zu verstehen, d. h. sie sind ohne Rücksicht auf Existenz– und Konvergenzbedingungen angegeben.
| Funktionstyp | Art der Transformation | Formel | Entwicklung in Frequenzkomponenten |
|---|---|---|---|
 |
Diskrete Fourier-Transformation | 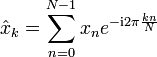 |
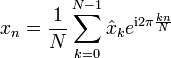 |
 |
Fourier-Reihe | 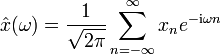 |
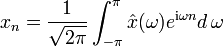 |
![x:[-\pi,\pi]\to\mathbb{C}](/pictures/dewiki/54/655e0f06e9fa5041642a258fe69d91ee.png) |
Fourier-Reihe | 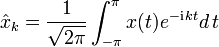 |
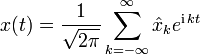 |
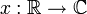 |
kontinuierliche Fourier-Transformation | 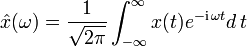 |
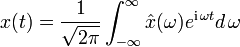 |
Man kann in der Transformation einen beliebigen positiven Faktor hinzufügen, muss diesen dann aber in der Entwicklungsformel wieder herausdividieren. Oft wählt man die Faktoren so, dass die Entwicklung nach einem orthonormalen System erfolgt, bzw. die Transformation und Entwicklung als lineare Abbildungen unitär sind. Dies ist in der Tabelle in den drei letzten Zeilen der Fall.
Diskrete Fourier-Transformation
→ Hauptartikel: Diskrete Fourier-Transformation
Es gibt keine Einschränkungen in der Anwendung der Transformation und der Entwicklungsformel. Sind F, T positive Zahlen mit FT=1/N, und sind M,L beliebige ganzzahlige Verschiebungen, so kann eine allgemeinere Variante der Transformationsformeln angegeben werden. Mit tn = nT und ωk = k(2πF) gilt
Zeitdiskrete Fourier-Transformation
→ Hauptartikel: Fourier-Reihe
Ist die Folge 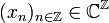 absolut summierbar, d. h.
absolut summierbar, d. h.  , so konvergiert die Fourier-Reihe in der Transformationsformel. Der Grenzwert der Reihe ist eine stetige Funktion, so dass auch die Integrale existieren. Da die Funktionen
, so konvergiert die Fourier-Reihe in der Transformationsformel. Der Grenzwert der Reihe ist eine stetige Funktion, so dass auch die Integrale existieren. Da die Funktionen 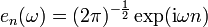 ein Orthonormalsystem bilden, erhält man aus der Zerlegungsformel wieder die Ausgangsfolge zurück. Verfolgt man dieses Argument weiter, so kann man diese Transformation auch für Folgen definieren, deren Reihe der Betragsquadrate endlich ist, d. h.
ein Orthonormalsystem bilden, erhält man aus der Zerlegungsformel wieder die Ausgangsfolge zurück. Verfolgt man dieses Argument weiter, so kann man diese Transformation auch für Folgen definieren, deren Reihe der Betragsquadrate endlich ist, d. h. 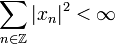 .
.
Für positive F, T mit FT=1 kann wieder eine allgemeinere Transformationsformel angegeben werden. Seien tn = nT Zeitpunkte mit Abstand T, dann gilt:
Fourier-Reihen für Funktionen auf einem Intervall
→ Hauptartikel: Fourier-Reihe
Jede stetige Funktion, welche über einem Intervall [0,T] definiert ist, lässt sich in eine Fourier-Reihe entwickeln, d. h. beide Seiten der Transformation existieren. Mit der Grundfrequenz F=1/T und den Kreisfrequenzen ωk = k(2πF) gilt:
Es können allgemeinere Typen von Funktionen in eine Fourier-Reihe entwickelt werden, so abschnittsweise stetige, beschränkte Funktionen oder allgemeiner messbare quadratintegrable Funktionen.
Kontinuierliche Fourier-Transformation
→ Hauptartikel: Kontinuierliche Fourier-Transformation
Die kontinuierliche Fourier-Transformation ist definiert durch
Die Rücktransformation (Fourier-Synthese oder inverse Fourier-Transformation) lautet analog dazu:
In der Literatur findet man auch andere Definitionen, die als Vorfaktor statt 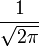 nur
nur 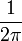 oder 1 haben. Dies hängt von den jeweils verwendeten Normierungskonventionen ab. Die hier verwendete Variante hat den ästhetischen Vorteil, dass der Vorfaktor bei Hin- und Rücktransformation gleich ist. Außerdem vereinfacht sie die Darstellung des Satzes von Plancherel:
oder 1 haben. Dies hängt von den jeweils verwendeten Normierungskonventionen ab. Die hier verwendete Variante hat den ästhetischen Vorteil, dass der Vorfaktor bei Hin- und Rücktransformation gleich ist. Außerdem vereinfacht sie die Darstellung des Satzes von Plancherel:
Diese Bedingung ist z. B. in der Physik wichtig für die Energieerhaltung durch die Fourier-Transformation. Mathematisch gesehen bedeutet die Gleichung, dass die Fourier-Transformation eine unitäre Abbildung ist.
Manchmal, z. B. in der Signaltheorie, bevorzugt man die – ebenfalls energieerhaltende – Version der Fourier-Transformation, bei der die – auch Spektralfunktion genannte – Fourier-Transformierte von der Frequenz statt der Winkelgeschwindigkeit abhängt:
Die Beziehung zwischen beiden Arten der Fourier-Transformation wird durch  vermittelt.
vermittelt.
Die Rücktransformation lautet dann
Da hier über die Variable ν statt ω integriert wird, entfällt in dieser Darstellungsform der Vorfaktor.
Existenz der Fourier-Transformierten
Hinreichend, aber nicht notwendig für die Konvergenz des Fourier-Integrals ist die absolute Integrierbarkeit der Zeitfunktion f(t), d. h. f ist Borel-messbar und Lebesgue-integrierbar, kurz: liegt in 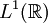 .
.
Ist diese Bedingung erfüllt, so ist die Fourier-Transformierte F von f eine stetige, beschränkte Funktion von  nach
nach  , es gilt sogar
, es gilt sogar  für
für 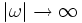 .
.
Dass die Bedingung nicht notwendig ist, sieht man zum Beispiel an der Sinc-Funktion sin(t) / t.. Diese ist nicht absolut integrierbar, hat aber eine Fourier-Transformierte.
Es existiert die Fourier-Transformierte ferner für jede quadratintegrierbare Funktion (und ist für diese normerhaltend, s. u.). Auch für Distributionen wie die Delta-Distribution lässt sich eine Fourier-Transformiertion definieren.
Rechenregeln
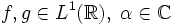 .
.
Da 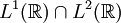 dicht in
dicht in 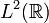 liegt, erlaubt es die Plancherel-Identität, die Fourier-Transformation als unitären Operator auf dem Hilbertraum
liegt, erlaubt es die Plancherel-Identität, die Fourier-Transformation als unitären Operator auf dem Hilbertraum 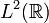 zu definieren, obwohl das Fourier-Integral für Funktionen aus
zu definieren, obwohl das Fourier-Integral für Funktionen aus 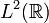 nicht mehr in jedem Punkt konvergieren muss.
nicht mehr in jedem Punkt konvergieren muss.
Varianten der Fourier-Transformation
Die verschiedenen Begriffe in diesem Zusammenhang werden leider in der Literatur nicht einheitlich gebraucht, und es existieren mehrere Namen für den gleichen Vorgang. So nutzt man Fourier-Transformation sehr oft als Synonym der kontinuierlichen Fourier-Transformation, und mit Fourier-Analyse wird oft die Zerlegung in eine Fourier-Reihe gemeint, manchmal aber auch die kontinuierliche Transformation.
Je nach den Eigenschaften der zu untersuchenden Funktion gibt es im wesentlichen drei Varianten (auf Grund der oben genannten Unschärfe der Begriffe erhebt die Liste keinen Anspruch auf vollständige Richtigkeit):
Man erhält bei allen Transformationen ein Frequenzspektrum, das je nach Variante diskret (unendlich scharfe Linien) oder kontinuierlich ist:
| Variante | Definitionsmenge von f | Periodizität von f | Frequenzspektrum |
|---|---|---|---|
| Fourier-Reihe | kontinuierliches Intervall | periodisch | diskret |
| Kontinuierliche Fourier-Transformation | kontinuierlich | aperiodisch | kontinuierlich |
| Diskrete Fourier-Transformation | diskret, endlich | periodisch | diskret, endlich |
Zur Berechnung der diskreten Fourier-Transformation wird oft die schnelle Fourier-Transformation (FFT) verwendet, ein Algorithmus, bei dem die Anzahl der Rechenschritte zur Berechnung der Fourier-Koeffizienten wesentlich kleiner ist als bei einer direkten Implementation der Integration.
Wegen der Bedeutung der Fourier-Transformation in der Signalverarbeitung sind Signalprozessoren für die Berechnung der Fourier-Transformation optimiert.
Mathematische Motivation
(Dieser Abschnitt setzt über die Schulmathematik des Gymnasiums hinaus nur Kenntnisse im Rechnen mit komplexen Zahlen sowie die Euler-Formel voraus.)
Mathematische Grundlagen
Wir betrachten stetige, von der Zeit t reell abhängige Funktionen bzw. Vorgänge (z. B. als vektorwertige Funktionen) f(t), die sich nach einer Zeit T wiederholen, also periodisch mit Periode T sind, f(t+T)=f(t). Joseph Fourier postulierte in seiner Arbeit, dass sich f aus periodischen, harmonischen Schwingungen, also Sinus- oder Kosinusfunktionen, verschiedener Phase und Amplitude und genau definierter Frequenz zusammensetzen lässt. Betrachten wir eine solche zusammengesetzte Funktion mit (N+1) Summanden:

Die einzelnen Schwingungen haben die Kreisfrequenz nω, also die Frequenz nω / 2π. Damit hat die erste Schwingung (Grundschwingung) die Frequenz 1 / T, die nächsten 2 / T, 3 / T, …
Weil ein Sinus nur ein phasenverschobener Kosinus ist, konnte die Reihendarstellung auf Kosinus-Funktionen beschränkt werden. Wir erhalten sofort auch die Sinusterme, wenn wir die Additionstheoreme benutzen:
Mit a0: = A0, 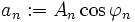 und
und 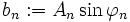 erhalten wir eine phasenfreie Darstellung
erhalten wir eine phasenfreie Darstellung
Im nächsten Schritt soll die Summe mit Hilfe komplexer Zahlen umgeschrieben werden. Es sind dann komplexe Koeffizienten erlaubt, und die Reihe wird komplexwertig. Sofern reelle Funktionen betrachtet werden, kann diese als Realteil der Summe zurückgewonnen werden. Aus der Euler-Formel oder auch nach der Definition der trigonometrischen Funktionen mit der Exponentialfunktion folgt
somit
Mit den komplexen Koeffizienten c0: = a0, 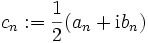 und
und 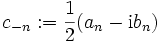 für n>0 erhalten wir eine Summe mit auch negativen Indizes
für n>0 erhalten wir eine Summe mit auch negativen Indizes
Fourier-Reihe
Wir kennen jetzt also die trigonometrische Summe in verschiedenen Darstellungen. Es war aber gefragt, eine periodische stetige Funktion mittels solch einer Summe zu approximieren. Dazu stellen wir fest, dass die komplexen Koeffizienten cn, und damit auch die der anderen Darstellungen, sich aus der Summenfunktion zurückgewinnen lassen.
Dazu wird die obige Gleichung mit e − imωt multipliziert und sodann auf beiden Seiten über dem Intervall [0,T], d. h. über eine Periode, integriert. Mit Umformungen erreicht man folgende Aussage:
Daraus folgt 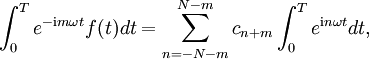
und für das n-te Integral auf der rechten Seite gilt:
Wegen ωT = 2π gilt nun aber einωT = (e2πi)n = 1, also 
Insgesamt vereinfacht sich das Integral zu
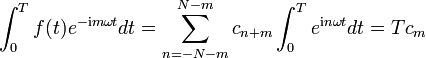
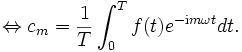
Wir können nun versuchen, die trigonometrische Summe durch eine beliebige stetige periodische Funktion f zu ersetzen, die Koeffizienten nach obigen Formeln zu bestimmen und die mit diesen Koeffizienten gebildeten trigonometrischen Summen mit der Ausgangsfunktion vergleichen:
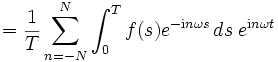


Die Funktion 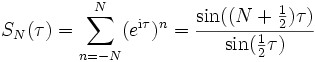 ist der Dirichlet-Kern.
ist der Dirichlet-Kern.
Konvergenz der Fourier-Reihe
Die so definierte Reihe <fN > ist allerdings nutzlos, wenn sie nicht gegen die ursprüngliche Funktion konvergiert. Tatsächlich konvergiert sie für sehr viele Funktionen, unter anderem für alle differenzierbaren Funktionen oder alle quadratintegrierbaren Funktionen, und zwar im erstgenannten Fall punktweise, im letztgenannten Fall allerdings nur „fast überall“, d. h. mit folgender Definition: 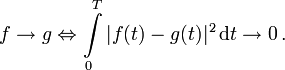 Auch in diesem Fall soll wie ganz am Anfang das Gleichheitszeichen benutzt werden.
Auch in diesem Fall soll wie ganz am Anfang das Gleichheitszeichen benutzt werden.
Wir können in diesem Sinne also zusammenfassen:
Aperiodische Vorgänge (Fourier-Integral)
Voraussetzung für die hergeleitete Fourier-Reihe ist die Periodizität von f(t) über dem Zeitintervall T. Selbstverständlich gibt es auch nichtperiodische Funktionen, die diese Voraussetzung für kein endliches Zeitintervall erfüllen. Wie schon gezeigt, hat die n-te Oberschwingung die Frequenz n / T. Die Differenz der n-ten Oberfrequenz von der vorherigen ist n / T − (n − 1) / T = 1 / T, das heißt die Oberfrequenzen haben den Abstand 1 / T. Für T gegen unendlich geht ihr Abstand gegen Null – die Summe wird im Grenzfall zum Riemann-Integral.
Das Fourier-Integral, die kontinuierliche Fourier-Transformation, ist also gegeben durch
mit
Aus der Folge an ist nun das kontinuierliche Spektrum a(ω) geworden. Man bezeichnet genau genommen die zweite Transformation als Fourier-Transformation, die erste, deren inverse, ist die Fourier-Synthese.
Die zweite Gleichung kann analog wie für die Reihe hergeleitet werden.
Das angegebene Beziehungspaar gilt u. a. erneut für quadratintegrierbare Funktionen.
Differentialgleichungen
Die Fourier-Transformation wird oft eingesetzt, um Differentialgleichungen zu lösen. Denn die einx bzw. die sin(nx),cos(nx) sind Eigenfunktionen der Differentiation, und die Transformation wandelt lineare Differentialgleichungen mit konstanten Koeffizienten in normale algebraische Gleichungen um.
So ist zum Beispiel in einem linearen zeitinvarianten physikalischen System die Frequenz eine Erhaltungsgröße, und das Verhalten kann für jede Frequenz einzeln gelöst werden. Die Anwendung der Fourier-Transformation auf die Differentialgleichung ergibt den Frequenzgang des Systems.
Verallgemeinerung
(Der folgende Abschnitt setzt Kenntnisse in linearer Algebra voraus.)
Allgemeine Betrachtung
Als verallgemeinerte Fourier-Transformation wird jede Zerlegung einer Funktion in ein System von Basisfunktionen bezeichnet. Solche Zerlegungen finden u. a. im Apparat der Quantenmechanik eine wichtige Anwendung. Durch die folgende abstrakte Betrachtung gewinnt man wichtige Einsichten in die eigentliche Bedeutung der Fourier-Transformation, die elementare Herleitung in den vorangegangenen Abschnitten erscheint in einem neuen Licht.
Man betrachte die zu transformierenden Funktionen (wie oben zunächst Funktionen mit der Periodizität T) als Elemente eines „Vektorraums mit Skalarprodukt“. Dass die Vektorraumaxiome erfüllt sind, erkennt man schon durch Hinschreiben; nun steht die ganze Macht der Theorie der linearen Algebra zur Verfügung (wobei der betrachtete Raum von unendlicher Dimension ist).
Als geeignetes Skalarprodukt zweier Funktionen definiert man wie üblich das Integral des Produktes über einem von der Anwendung abhängigen Intervall. Es bietet sich an, über die Periode von 0 bis T zu integrieren:

Dabei ist 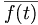 das Konjugiert-komplexe von f(t). So wie (1,0,0), (0,1,0), (0,0,1) eine Basis des dreidimensionalen reellen Anschauungsraumes
das Konjugiert-komplexe von f(t). So wie (1,0,0), (0,1,0), (0,0,1) eine Basis des dreidimensionalen reellen Anschauungsraumes 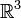 ist, besitzt auch der Funktionenraum wie jeder Vektorraum eine Basis. Während im endlich-dimensionalen die Basen genau die minimalen Erzeugendensysteme sind, muss bei den unendlich-dimensionalen Funktionenräumen durch ein Funktionensystem das Kriterium der Vollständigkeit (im Sinne der Funktionalanalysis) erfüllt sein.
ist, besitzt auch der Funktionenraum wie jeder Vektorraum eine Basis. Während im endlich-dimensionalen die Basen genau die minimalen Erzeugendensysteme sind, muss bei den unendlich-dimensionalen Funktionenräumen durch ein Funktionensystem das Kriterium der Vollständigkeit (im Sinne der Funktionalanalysis) erfüllt sein.
Gegeben sei das vollständige Basissystem B. Man kann jede Funktion aus dem Funktionenraum als Linearkombination der Basisfunktionen bn darstellen:
Praktisch möglich ist die Bestimmung der Koeffizienten λn aber nur, wenn das Basissystem ein Orthogonalsystem ist, und ist sogar besonders einfach, wenn es ein Orthonormalsystem ist, d. h. wenn für alle 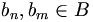 gilt
gilt
Denn wie man die Komponente eines Vektors in x-Richtung im 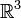 durch
durch
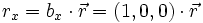
erhält – denn auch das obige Beispiel ist eine Orthonormalbasis – so erhält man allgemein den Faktor λn, die „Komponente in Richtung“ von bn, durch
wenn die bn ein vollständiges Orthonormalsystem, eine Orthonormalbasis, bilden. Der Beweis ist einfach: Denn unter Ausnutzung der Linearitätseigenschaften des Skalarprodukts erhält man
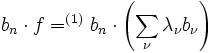

Es sei angemerkt, dass der Vergleich mit dem  hier eher didaktischer Natur ist, denn die Beispielbasis ist genau genommen eine sog. Hamelbasis, während die Orthonormalbasis des untersuchten Funktionenraumes keine solche ist – der Raum besitzt auch eine Hamelbasis, die allerdings überabzählbar und von keinem praktischen Interesse ist. Die Orthonormalbasis hat abzählbare Dimension und sie ist vollständig, d. h. ihre lineare Hülle liegt dicht im Vektorraum, ist aber nicht notwendigerweise gleich dem Raum. Deshalb lässt sich nicht unbedingt jedes Element des Raums durch eine endliche, wohl aber durch eine unendliche Summe darstellen.
hier eher didaktischer Natur ist, denn die Beispielbasis ist genau genommen eine sog. Hamelbasis, während die Orthonormalbasis des untersuchten Funktionenraumes keine solche ist – der Raum besitzt auch eine Hamelbasis, die allerdings überabzählbar und von keinem praktischen Interesse ist. Die Orthonormalbasis hat abzählbare Dimension und sie ist vollständig, d. h. ihre lineare Hülle liegt dicht im Vektorraum, ist aber nicht notwendigerweise gleich dem Raum. Deshalb lässt sich nicht unbedingt jedes Element des Raums durch eine endliche, wohl aber durch eine unendliche Summe darstellen.
Der angegebene Funktionenraum, wie er z. B. in der Quantenmechanik verwendet wird, ist ein Hilbertraum. Üblicherweise betrachtet man solche Hilberträume, die eine abzählbare Orthonormalbasis besitzen, das heißt, die wie oben eine Orthonormalbasis (bn)n besitzen, deren Indizes aus einer endlichen Menge oder aus den natürlichen oder ganzen Zahlen stammen. Dies ist äquivalent zur sogenannten Separabilität des Hilbertraums.
Zusammenfassend gilt nach (1) und (3) für eine beliebige Funktion f aus dem Funktionenraum und für jedes vollständige Orthonormalsystem B
wobei die Konvergenz im Sinne des Hilbertraums zu verstehen ist, im Allgemeinen liegt keine punktweise oder gar gleichmäßige Konvergenz vor.
Fourier-Transformation als Beispiel
Den Weg zurück zur Fourier-Transformation findet man, indem man zunächst die Funktionen b'n = einωt untersucht, nach denen ja entwickelt wird. Sie sind ein Orthogonalsystem, denn mit 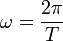 folgt
folgt
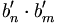
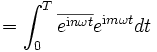
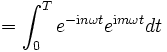
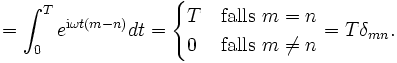
(Das Integral wurde schon in der elementaren Herleitung gelöst.)
Für die Norm findet man
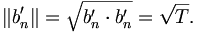
Offenbar sind die b'n orthogonal, orthonormal sind aber erst die 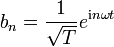 . Nach der allgemeinen Herleitung (4) gilt also für eine Funktion f(t)
. Nach der allgemeinen Herleitung (4) gilt also für eine Funktion f(t)
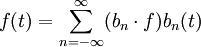
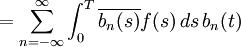
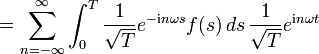
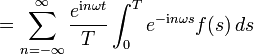
was genau dem Resultat der elementaren Herleitung entspricht. Wie dort der Konvergenzbeweis, fehlt auch hier nur noch der Beweis, dass das Basissystem für weite Funktionenklassen vollständig ist. Dies ist (ohne Beweis) der Fall, wenn keiner der Indizes n ausgelassen wird.
Literatur
Weblinks
Siehe auch
Wikimedia Foundation.
