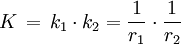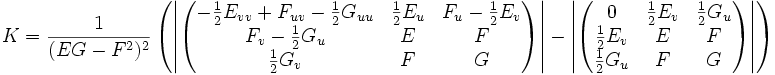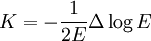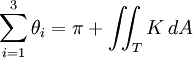Gausskrümmung

In der Theorie der Flächen im dreidimensionalen Raum (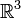$\mathbb{R}^3$), einem Gebiet der Differentialgeometrie, ist die gaußsche Krümmung (das gaußsche Krümmungsmaß), benannt nach dem Mathematiker Carl Friedrich Gauß, der wichtigste Krümmungsbegriff neben der mittleren Krümmung.

Definition

Gegeben seien eine reguläre Fläche im 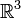$\mathbb{R}^3$ und ein Punkt dieser Fläche. Die gaußsche Krümmung K der Fläche in diesem Punkt ist das Produkt der beiden Hauptkrümmungen k₁ und k₂.

• $K \, = \, k_1 \cdot k_2 = \frac{1}{r_1} \cdot \frac{1}{r_2}$

Dabei sind r₁ und r₂ die beiden Hauptkrümmungsradien.

Das Krümmungsmaß ist positiv (K > 0), wenn beide Radien auf derselben Seite liegen (z.B. bei doppelt gekrümmten Flächentragwerken wie Kuppeln). Liegen die Mittelpunkte zu den Radien auf unterschiedlichen Seiten wie bei einer Sattelfläche, ist das Krümmungsmaß negativ (K < 0).

Beispiele

• Im Falle einer Kugel(oberfläche) mit Radius r ist die gaußsche Krümmung gegeben durch K = 1 / r².

• In einem beliebigen Punkt auf der gekrümmten Fläche eines geraden Kreiszylinders ist die gaußsche Krümmung gleich 0.

• In einem beliebigen Punkt auf der gekrümmten Fläche eines geraden Kreiskegels ist die gaußsche Krümmung gleich 0.

• Ist X = X(u,v) = (u,v,f(u,v)) ein Graph über der (u,v)−Ebene, so berechnet sich die gaußsche Krümmung durch die Formel

$K = \frac{f_{uu} f_{vv} - f_{uv}^2}{{(1+f_u^2+f_v^2)}^{2}}$,

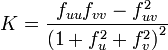wobei die Indizes partielle Ableitungen bezeichnen.

Eigenschaften

• Sind E, F, G bzw. L, M, N die Koeffizienten der ersten bzw. zweiten Fundamentalform, so gilt folgende Formel:

$K = \frac{LN - M^2}{EG - F^2}$

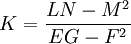
• Die gaußsche Krümmung hängt nur von der inneren Geometrie der gegebenen Fläche ab (siehe Theorema egregium von C. F. Gauß). Dieser Satz ist ein Korollar aus der:

• Formel von Brioschi:

$K = \frac{1}{(EG-F^2)^2} \left( \left|\begin{pmatrix} -\frac{1}{2}E_{vv} + F_{uv} - \frac{1}{2}G_{uu} &amp;amp; \frac{1}{2}E_u &amp;amp; F_u-\frac{1}{2}E_v\\ F_v-\frac{1}{2}G_u &amp;amp; E &amp;amp; F\\ \frac{1}{2}G_v &amp;amp; F &amp;amp; G \end{pmatrix}\right| - \left|\begin{pmatrix} 0 &amp;amp; \frac{1}{2}E_v &amp;amp; \frac{1}{2}G_u\\ \frac{1}{2}E_v &amp;amp; E &amp;amp; F\\ \frac{1}{2}G_u &amp;amp; F &amp;amp; G \end{pmatrix}\right| \right)$

Dabei sind E, F und G die Koeffizienten der ersten Fundamentalform. Die Bezeichnungen E_u, F_uv usw. stehen für erste und zweite partielle Ableitungen nach den Parametern u und v, mit denen die gegebene Fläche parametrisiert wird. Diese Gleichung ist unter anderem eine der notwendigen Integrationsbedingungen der Gauß-Weingarten-Gleichungen.

• Wenn die erste Fundamentalform isotherm parametrisiert ist, d.h. es gilt 0 < E = G und F = 0, dann schreibt sich

$K = -\frac{1}{2E} \Delta \log E$

mit dem Laplaceoperator

$\Delta = \frac{\partial^2}{\partial u^2}+\frac{\partial^2}{\partial v^2}$.

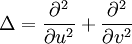Totale Krümmung

Das Oberflächenintegral der Gauß-Krümmung über den Bereich einer Oberfläche nennt man totale Krümmung.

$\sum_{i=1}^3 \theta_i = \pi + \iint_T K \,dA$

Sie besitzt bei einem ebenen Dreieck den Wert π, ebenso bei jedem geschlossenen Kurvenintegral (Weginteral über geschlossene Kurve, auch Umfangsintegral genannt) in einer Euklidischen Ebene (die Gesetze bleiben ebenso gültig im n-dimensionalen Raum).

Umgekehrt nennt man ein genau diese Bedingung für jedes geschlossenes Kurvenintegral (in 3D: Hüllenintegral) erfüllendes Feld ein konservatives Potentialfeld oder Laplacefeld (s. Laplacegleichung). Das wird auch quellenfreies Feld genannt.

Überschreitet oder unterschreitet die Summe der Winkel bei einer positiven oder negativen Krümmung den Wert π, nennt man ein solches Feld ein nicht quellenfreies oder Poisson-Feld (s. Poissongleichung).

Der einfache Wert π entsteht dadurch, dass einem angenommenen Radius für jeden beliebig gewählten Umlaufsweg der (jeder Krümmung zugeordnete reziproke) Bezugswert R = 1 zugeordnet werden darf, Normierung genannt.

Im allgemeinsten Fall entsteht aber ein Tensor, ein hier sog. Krümmungstensor (s. Riemannscher Krümmungstensor), als Wirkung eines allgemeinen Feldes - aus unterschiedlichen Richtungen gesehen - mit dem sog. Energie-Impuls-Tensor, dem als Ursache innere Energiequellen zugeordnet sind, z.B. innere Massequellen, incl. verteilten Gasen.

Gauß'scher Integralsatz

Der Satz von Gauß (auch gaußscher Integralsatz, Satz von Gauß-Ostrogradski, oder Divergenzsatz) ist eine spezielle Anwendung. Der Satz gilt als wichtige Basis für die Allgemeine Relativitätstheorie.

Der Satz von Gauß besagt, dass die Integration beliebig verteilter Quellen und Senken über ein Volumen - nur im Inneren - der Divergenz eines Vektorfeldes gleich ist dem Hüllenintegral über die dadurch definierte geschlossene Oberfläche des gleichen Volumens: Die Summe aller Quellen und Senken im Inneren eines Volumens bewirkt einen gleichen vektoriellen Fluss an der Oberfläche des Volumens.

Bei inkompressiblen Medien (Flüssigkeiten) ist die vektorielle Richtung des Durchflusses - als dann allein wirksame Vektorkomponente genau Richtung Oberfläche - stets gleichgerichtet mit dem senkrecht auf der Oberfläche stehenden Oberflächenvektor. Vereinfacht wird die Berechnung durch das dann allein noch wirksame sog. Skalarprodukt als reine Wirkung gleichgerichteter Vektorkomponenten. Dies erlaubt Vereinfachung - sog. Tensorverjüngung - von im Allgemeinfall Produkten von zwei Tensoren als allg. Produkt von kovarianten bzw. kontravarianten "Vektorsätzen" (s. Kovarianz (Physik) und dort Abs. "Kontravarianz"), wie folgt:

Kompressible Gase sind in jeder Richtung elastisch verformbar, zudem entstehen darin auch Schallwellen. Mach'sche Gesetze (s. Gasdynamik, besonders des Machschen Prinzips) beschreiben sie. Die Kraftwirkungen sind dann nicht mehr einfach nur mit einem Vektor zu beschrieben. Weil elastische Kräfte dann sogar in jeder Richtung verschieden wirken, werden diese mit einem - unabhängig orthogonal gewählten - "Vektorsatz" in 2,3,4...n Dimensionen beschrieben, einem sog. Tensor.

Krümmungstensor, Wirkung des Energie-Impuls-Tensors

Die Idee Einsteins war es, mit einem vierdimensionalen Ansatz - nur unter Einbeziehung einer zusätzlichen Koordinate ct - unmittelbar einen solchen Krümmungstensor einfach als Wirkung des Energie-Impuls-Tensors im Inneren eines umschlossenen Volumens zu sehen, nun in einer vereinfachten elementaren Form

G_μν = κT_μν

mit der Wirkung, dass eine Krümmung im 4D-Raum sich im 3D-Raum nur als reine Scheinkraft mit einer Gravitation auswirkt.

Kosmologische Krümmung

Eine dazu relevante sog. kosmologische Konstante ist ein von Einstein mathematisch frei gewählter Korrekturfaktor zur Anpassung einer realen Krümmung des Universums (siehe Allgemeine Relativitätstheorie, Abs. "Raumzeitkrümmung") und bewirkt – statt z.B. einem Zusammenfallen durch Gravitation oder Expansion durch eine Art "kosmischem Gasdruck" – als Ergebnis zumindest ein von Einstein zunächst erwünschtes labiles Gleichgewicht oder sogar eine Expansion gemäß Urknall.

Bemerkung

• Einen Zusammenhang zwischen der Gaußschen Krümmung und der geodätischen Krümmung vermittelt der Satz von Gauß-Bonnet.