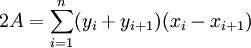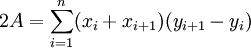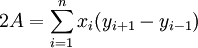- Gausssche Trapezformel
-
Mit Hilfe der gaußschen Trapezformel (nach Carl Friedrich Gauß) ist es möglich, die Fläche zwischen mehreren auf eine Messungslinie bezogenen/koordinierten Punkten, also beispielsweise die Fläche eines einfachen Polygons, zu berechnen. Durch die Zerlegung der gesuchten Fläche in einzelne auf die Messungslinie bezogenen Trapeze erfolgt die Berechnung.
Wortformel: Die doppelte Fläche entspricht der Summe des aktuellen Rechtswertes und des darauf folgenden, multipliziert mit der Differenz aus aktuellem Hochwert und folgendem Hochwert.
oder:
Die doppelte Fläche entspricht der Summe des aktuellen Hochwertes und des darauf folgenden, multipliziert mit der Differenz aus folgendem Rechtswert und aktuellem Rechtswert.
wobei die Indizes, die größer als n sind, immer modulo n betrachtet werden müssen, d.h. mit xn + 1 ist x1 gemeint.
Erfolgt die Flächenberechnung im Uhrzeigersinn, so bildet sich eine negative Fläche. Im Gegensatz hierzu wird das Ergebnis bei Berechnung im mathematisch positiven Drehsinn, d.h. entgegen dem Uhrzeigersinn, positiv.
Beispiel
Die Dokumentation des Rechenweges kann auf unterschiedliche Art und Weise geschehen. Zur Vereinfachung dieser Schreibweise dienen z.B. innerhalb des Vermessungswesens vorgefertigte Vordrucke.
Zerlegt man die auf dem Bild zu sehende Einzelfläche A in die 4 Teilflächen AI,AII,AIII und AIV, so erhält man folgende Formel
- A = AII + AIII − AI − AIV
Somit ist
- 2A = (y2 + y3)(x2 − x3) + (y3 + y4)(x3 − x4) − (y2 + y1)(x2 − x1) − (y1 + y4)(x1 − x4).
Setzt man jedoch die gegebenen Rechts- und Hochwerte vorzeichentreu in die zuerst genannte Formel ein, so ergibt sich durch
- 2A = (y1 + y2)(x1 − x2) + (y2 + y3)(x2 − x3) + (y3 + y4)(x3 − x4) + (y4 + y1)(x4 − x1)
ebenfalls die gesuchte Einzelfläche.
Dreiecksformel
Die gaußsche Dreiecksformel ergibt sich durch das Ausklammern und Umstellen der Trapezformel. Die Indizes, die größer als n sind, müssen wieder modulo n betrachtet werden, d.h. mit xn + 1 ist x1 gemeint und mit xn + 2 ist x2 gemeint.
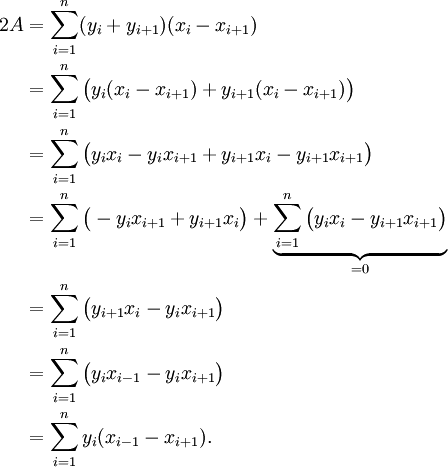
analog lässt sich
zu
umformen.
Die Wortformel:
Die doppelte Fläche entspricht dem Produkt aus dem aktuellen Rechtswert und der Differenz aus vorherigem Hochwert und folgendem Hochwert.
oder:
Die doppelte Fläche entspricht dem Produkt aus dem aktuellen Hochwert und der Differenz aus vorherigem Rechtswert und folgendem Rechtswert.
Anwendung
Im Regelfall dient sie zur Flächenbestimmung im Gauß-Krüger-Koordinatensystem. Hierbei muss jedoch die Flächenverzerrung abhängig vom Abstand zum Hauptmeridian berücksichtigt werden.
Formel zur Berücksichtigung der Flächenverzerrung:
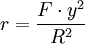
- r = Flächenreduktion
- F = Ausgangsfläche
- y = Abstand zum Hauptmeridian
- R = Erdradius (geodätischer Erdradius = 6381 km)
Wikimedia Foundation.