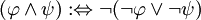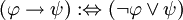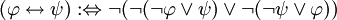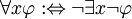- Gentzenkalkül
-
Der Sequenzenkalkül (manchmal auch Gentzenkalkül) ist ein von Gerhard Gentzen entwickelter, primär für metalogische Zwecke konzipierter logischer Kalkül.
Inhaltsverzeichnis
Notationen und Konventionen
In diesem Artikel werden folgende Zeichen verwendet:
- Γ,Φ ... (Formelmengen)
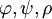 ... (Formeln)
... (Formeln)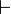 ... (Zeichen für Herleitungsbeziehung)
... (Zeichen für Herleitungsbeziehung)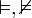 ... (Zeichen für die Beziehung der logischen Wahrheit/Folge)
... (Zeichen für die Beziehung der logischen Wahrheit/Folge) ... (Negationszeichen)
... (Negationszeichen)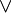 ... (Adjunktionszeichen)
... (Adjunktionszeichen)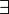 ... (Existenzquantor)
... (Existenzquantor)- (,) ... (Klammern als Hilfszeichen für mehr Übersichtlichkeit)
- ' ... (Kennzeichnung für die Erweiterung einer Formelmenge)
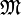 ... (Zeichen für Modell)
... (Zeichen für Modell)- s ... (Zeichen für Variablenbelegungsfunktion)
Es werden folgende Konventionen eingeführt:
- Mittels diverser Regeln lassen sich die übrigen Junktoren
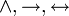 in Formeln umformen, die dann nur noch
in Formeln umformen, die dann nur noch  und
und 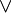 enthalten. Die Umformungregeln folgen:
enthalten. Die Umformungregeln folgen:
- Mittels einer Umformungsregel lässt sich der Quantor
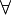 (Allquantor) wie folgt darstellen:
(Allquantor) wie folgt darstellen:
Von diesen Umformungen wird in den Beispielen Gebrauch gemacht.
Definition
Eine Sequenz ist eine endliche Abfolge von Formeln, formal <
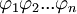 , wobei
, wobei 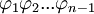 das Antezedens und
das Antezedens und 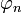 das Konsequens ist. Γ,Δ,... seien Variablen für Sequenzen.
das Konsequens ist. Γ,Δ,... seien Variablen für Sequenzen.Sei Φ eine Formelmenge und
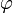 eine Formel.
eine Formel. 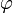 ist aus Φ herleitbar (kurz:
ist aus Φ herleitbar (kurz: 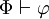 ) :gdw (genau dann wenn) es
) :gdw (genau dann wenn) es 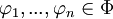 gibt, sodass
gibt, sodass 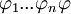 im Sequenzenkalkül herleitbar ist. (M.a.W.: Mittels Regeln werden die Sequenzen so lange manipuliert, bis man das gewünschte Ergebnis erhält.)
im Sequenzenkalkül herleitbar ist. (M.a.W.: Mittels Regeln werden die Sequenzen so lange manipuliert, bis man das gewünschte Ergebnis erhält.)Regeln des Sequenzenkalküls der Prädikatenlogik erster Stufe mit Identität
Die Regeln des Sequenzenkalküls der Prädikatenlogik erster Stufe mit Identität werden in folgende Gruppen eingeteilt:
Grundregeln, Junktorenregeln, Quantorenregeln und Identitätsregeln.
Grundregeln
Zu den Grundregeln gehören die Antezedensregel und die Annahmeregel.
Antezedensregel
 wobei gilt:
wobei gilt: 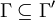 .
.In Worten: Man kann problemlos Annahmen hinzufügen.
Annahmeregel
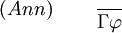 wobei gilt:
wobei gilt: 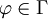
In Worten: Man kann Annahmen aus denselben schließen.
Junktorenregeln
Zu den Junktorenregeln gehören die Fallunterscheidung, die Kontradiktion, die Adjunktionseinführung im Antezedens und die Adjunktionseinführung im Konsequens.
Fallunterscheidung
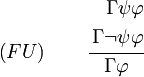
In Worten: Wenn man
 einerseits unter der Annahme von ψ und andererseits unter der Annahme von
einerseits unter der Annahme von ψ und andererseits unter der Annahme von  herleiten kann, darf man, ohne irgendeine Annahme über ψ oder
herleiten kann, darf man, ohne irgendeine Annahme über ψ oder  machen zu müssen, auf
machen zu müssen, auf 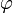 schließen.
schließen.Kontradiktion
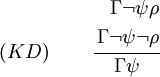
In Worten: Wenn
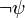 zu einem Widerspruch führt, dann darf auf ψ geschlossen werden.
zu einem Widerspruch führt, dann darf auf ψ geschlossen werden.Adjunktionseinführung im Antezedens
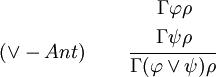
In Worten: Disjunktionen der Form
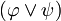 im Antezedens können auf zwei Weisen verwendet werden - einerseits im Fall
im Antezedens können auf zwei Weisen verwendet werden - einerseits im Fall 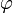 und andererseits im Fall ψ.
und andererseits im Fall ψ.Adjunktionseinführung im Konsequens
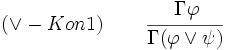
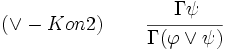
In Worten: Man darf immer das Konsequens durch eine Adjunktionseinführung abschwächen.
Quantorenregeln
Zu den Quantorenregeln gehören die Existenzeinführung im Konsequens und die Existenzeinführung im Antezedens.
Existenzeinführung im Konsequens
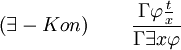
In Worten: Wenn man aus Γ herleiten kann, dass t eine durch
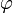 ausgedrückte Eigenschaft hat, dann darf man auch darauf schließen, dass etwas existiert, welches eine Eigenschaft hat, die durch
ausgedrückte Eigenschaft hat, dann darf man auch darauf schließen, dass etwas existiert, welches eine Eigenschaft hat, die durch 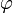 ausgedrückt wird.
ausgedrückt wird.Existenzeinführung im Antezedens
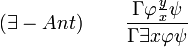 , wenn y in der Sequenz
, wenn y in der Sequenz 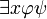 nicht frei vorkommt.
nicht frei vorkommt.Identitätsregeln
Zu den Identitätsregeln gehören die Reflexivität und die Substitutionsregel.
Reflexivität

In Worten: Die Äquivalenzrelation auf den Gegenstandsbereich D ist reflexiv.
Substitutionsregel
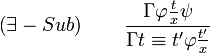
In Worten: Einsetzung von Identischem in Identisches.
Nützliche Herleitungen
Mit den oben aufgestellten Regeln des Sequenzenkalküls werden nun in endlichen Schritten einige nützliche Gesetze hergeleitet. (Zur Erinnerung: Herleitung ist gleichzusetzen mit Sequenzenmanipulation durch Anwendung der Regeln.) Diese Gesetze können dann problemlos verwendet werden, das heißt es reicht, deren Herleitung hier einmal zu zeigen. Hier werden folgende Gesetze gezeigt: der Satz vom ausgeschlossenen Dritten, die Trivialität, der Kettenschluss, die Kontraposition und der disjunktive Syllogismus. Zur Notation: Jede Herleitung ist in drei Spalten aufgeteilt. In der linken Spalte befindet sich die Nummerierung der einzelnen Modifikationen. Sie sind für eine unmissverständliche Bezugnahme durch andere Modifikationen nützlich. Die mittlere Spalte enthält die neue Modifikation, mit einer Abfolge von Sequenzen als Ergebnis. Die rechte Spalte enthält die Information, wie die Sequenz in der mittleren Spalte erreicht wurde. Dabei ist die Regel in Klammern geschrieben, und eventuell, durch ein Doppelpunkt eingeleitet (zu lesen als "angewendet auf"), sind die für das Ergebnis relevanten Zeilennummern notiert. Bsp.: "(Ant):1.,2." wird gelesen als "Antezedensregel, angewendet auf Zeile eins und zwei".
Satz vom ausgeschlossenen Dritten
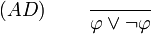
Herleitung:
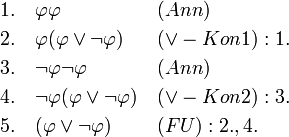
Trivialität
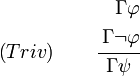
Herleitung:

Kettenschluss
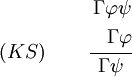
Herleitung:
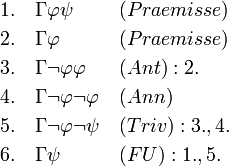
Anmerkung: Bei dieser Herleitung wurde die Regel (Triv) verwendet. An diesem Beispiel sieht man, dass eine hergeleitete Regel bloß einmal fehlerfrei hergeleitet zu werden braucht, um sie dann in Folge als eine Abkürzung zu verwenden. Durch die Verwendung der Regel (Triv) wurden z.B. fünf Herleitungsschritte (nämlich genau die fünf Schritte die man benötigt, um (Triv) herzuleiten) ausgespart.
Kontraposition
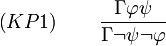
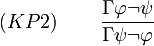
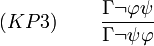
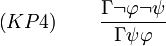
Herleitung von (KP1)((KP2)-(KP4) analog):
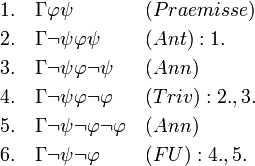
Disjunktiver Syllogismus
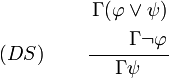
Herleitung:

Eigenschaften des Sequenzenkalküls
Korrektheit
Der Korrektheitssatz lautet wie folgt:
Für alle Formelmengen Φ und alle Formeln
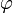 gilt: Wenn
gilt: Wenn 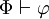 , dann
, dann 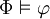 .
.Die Korrektheit des Sequenzenkalküls wird dadurch gezeigt, dass für jede einzelne Regel des Sequenzenkalküls gezeigt wird, dass sie korrekt ist, d.h., dass ein Modell
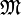 und eine Variablenbelegung s existieren, die die Regel wahr machen. Alle Korrektheitsbeweise zusammengenommen ergeben dann den Beweis des Korrektheitssatzes.
und eine Variablenbelegung s existieren, die die Regel wahr machen. Alle Korrektheitsbeweise zusammengenommen ergeben dann den Beweis des Korrektheitssatzes.Definitionen
Um den Korrektheitssatz zeigen zu können, müssen zuvor noch "Modell", "Variablenbelegung" und "wahrmachen" (logische Wahrheit) definiert werden.
Modell
Ein Modell ist ein geordnetes Paar
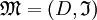 , sodass gilt:
, sodass gilt:- D ist eine nicht-leere Menge (die "Domäne" oder der "Gegenstandsbereich", über die/den die Quantoren laufen)
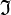 ist die Interpretationsfunktion für Prädikate, Funktionen und Konstanten (in der Folge nicht relevant)
ist die Interpretationsfunktion für Prädikate, Funktionen und Konstanten (in der Folge nicht relevant)
Variablenbelegung
Eine Variablenbelegung s über einem Modell
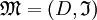 ist eine Funktion
ist eine Funktion  .
.Logische Wahrheit/Folge
Für alle Formeln
 und alle Formelmengen Φ gilt:
und alle Formelmengen Φ gilt:  folgt logisch aus Φ (kurz:
folgt logisch aus Φ (kurz:  ) gdw für alle Modelle
) gdw für alle Modelle 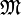 und alle Variablenbelegungen s über
und alle Variablenbelegungen s über 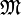 gilt: Wenn
gilt: Wenn 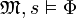 , dann
, dann 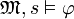 . (M.a.W.: Wenn es
. (M.a.W.: Wenn es 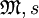 gibt, welche Φ wahrmachen, wird
gibt, welche Φ wahrmachen, wird 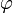 vom selben
vom selben 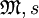 wahr gemacht.)
wahr gemacht.)Korrektheit der Regeln des Sequenzenkalküls
Die Korrektheit der Regeln des Sequenzenkalküls zeigt man, indem man die logische Wahrheit der Regeln zeigt. Dabei stützt man sich auf die Definition der logischen Wahrheit/Folge. Nun wird gezeigt, dass jede einzelne Regel des Sequenzenkalküls logisch wahr ist. (Es werden nicht alle Beiweise gezeigt. Es reicht lediglich einige wenige zu skizzieren. Die restlichen Beweise sind von der Struktur her ähnlich.)
Korrektheit von (Ant)
Angenommen,
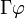 ist korrekt, d.h.
ist korrekt, d.h. 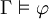 . Sei Γ' eine Formelmenge, sodass gilt:
. Sei Γ' eine Formelmenge, sodass gilt: 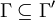 . Seien
. Seien 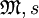 beliebig gewählt, sodass gilt:
beliebig gewählt, sodass gilt: 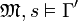 . Dann gilt auch
. Dann gilt auch 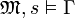 und laut Voraussetzung auch
und laut Voraussetzung auch 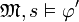 . Daraus folgt
. Daraus folgt 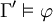 . Also ist
. Also ist 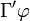 korrekt.
korrekt.Korrektheit von (Ann)
Wenn
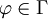 , dann gilt
, dann gilt 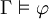 . Somit ist
. Somit ist 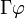 korrekt.
korrekt.Korrektheit von (FU)
Angenommen
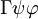 und
und 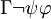 sind korrekt, d.h.
sind korrekt, d.h.  und
und 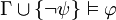 . Seien
. Seien 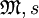 beliebig gewählt, sodass gilt:
beliebig gewählt, sodass gilt: 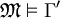 .
.Fall 1:
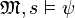 . Dann
. Dann 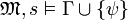 und somit nach Voraussetzung
und somit nach Voraussetzung 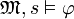 .
.Fall 2:
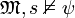 . Dann
. Dann 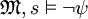 . Dann
. Dann 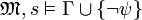 und somit nach Voraussetzung
und somit nach Voraussetzung 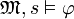 .
.In beiden Fällen gilt
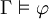 . Somit ist
. Somit ist 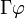 korrekt.
korrekt.Korrektheit von (KD)
Angenommen
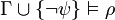 und
und 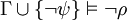 . Dann gilt für alle
. Dann gilt für alle 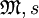 mit
mit 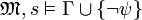 :
: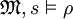 und
und 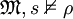 . Dann gibt es kein
. Dann gibt es kein 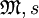 , sodass gilt:
, sodass gilt: 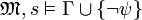 . Dann gilt für alle
. Dann gilt für alle 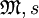 mit
mit 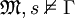 :
: 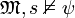 . Somit gilt
. Somit gilt 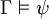 und somit ist Γψ korrekt.
und somit ist Γψ korrekt.
Hat man noch zusätzlich die restlichen Regeln bewiesen, also deren Korrektheit gezeigt, so ist der Korrektheitssatz bewiesen und es kann gesagt werden: Ist eine Formel im Sequenzenkalkül herleitbar, so ist diese Formel auch logisch wahr.Vollständigkeit
Das Kalkül ist außerdem auch noch vollständig. Das heißt es gilt:
Für alle Formelmengen Φ und alle Formeln
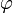 gilt: Wenn
gilt: Wenn 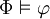 , dann
, dann 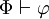 .
.Intuitiv bedeutet dies, dass alle wahren Sequenzen mit Hilfe der oben angegebenen Regeln hergeleitet werden können.
Beispiele
Zum Schluss sollen noch zwei Beispiele mit dem Sequenzenkalkül vorgeführt werden.
Beispiel 1
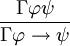
Herleitung:
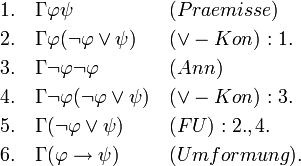
Beispiel 2
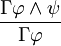
Herleitung:
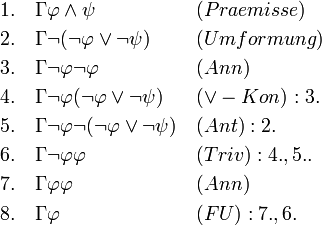
Literatur
- Ebbinghaus H.-D., Flum J., Thomas W.: Einführung in die mathematische Logik. Berlin: Springer-Verlag, 2007.
- Richter, M. M.: Logikkalküle. Stuttgart: Teubner Verlag, 1978.
Weblinks
- Sequent Calculus by Alex Sakharov MathWorld
- Jan von Plato: „The Development of Proof Theory: Natural deduction and sequent calculus“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
- Frederic Portoraro: „Automated Reasoning: Sequent Deduction“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
Wikimedia Foundation.