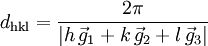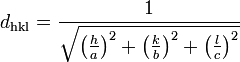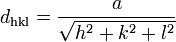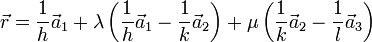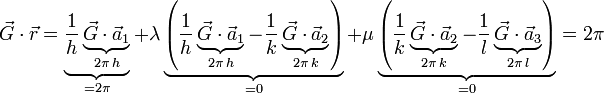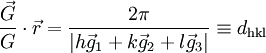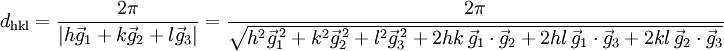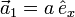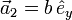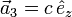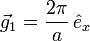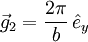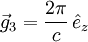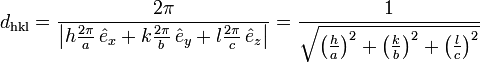- Gitterebenenabstand
-
Als Netz- oder Gitterebene bezeichnet man eine Ebene, die durch Punkte des Kristallgitters aufgespannt wird. Ihre Lage im Raum wird durch die Millerschen Indizes (hkl) beschrieben.
Ein Kristallgitter lässt sich als ganzzahlige Linearkombination der Basisvektoren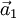 ,
, 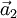 und
und 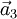 (Richtung der Kristallachsen) beschreiben. Eine Netzebene ist durch ihre Schnittpunkte mit den Kristallachsen festgelegt. Die Millerschen Indizes (hkl) bezeichnen die Ebene, die durch die drei Punkte
(Richtung der Kristallachsen) beschreiben. Eine Netzebene ist durch ihre Schnittpunkte mit den Kristallachsen festgelegt. Die Millerschen Indizes (hkl) bezeichnen die Ebene, die durch die drei Punkte 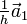 ,
, 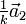 und
und 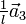 geht. Also schneiden die Kristallachsen des jeweiligen Kristallsystems die Ebenen gerade an den Kehrwerten der einzelnen Indizes. Ein Index von Null bezeichnet dabei einen Schnittpunkt im Unendlichen, d.h. der zugehörige Basisvektor ist parallel zur Ebene.
geht. Also schneiden die Kristallachsen des jeweiligen Kristallsystems die Ebenen gerade an den Kehrwerten der einzelnen Indizes. Ein Index von Null bezeichnet dabei einen Schnittpunkt im Unendlichen, d.h. der zugehörige Basisvektor ist parallel zur Ebene.Der reziproke Gittervektor
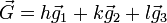 steht senkrecht auf der durch die Millerschen Indizes (hkl) definierten Netzebene. Die Vektoren
steht senkrecht auf der durch die Millerschen Indizes (hkl) definierten Netzebene. Die Vektoren 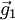 ,
, 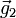 und
und 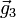 bilden die Basisvektoren des reziproken Gitters.
bilden die Basisvektoren des reziproken Gitters.Eine Netzebenenschar besteht aus allen parallel verlaufenden Netzebenen mit jeweils dem Netzebenenabstand dhkl. Dieser kann aus den Millerschen Indizes und den reziproken Gittervektoren berechnet werden:
Für Kristallsysteme mit rechtwinkligen Achsen, also orthorhombische und höher symmetrische Gitter (tetragonal und kubisch) gilt folgende Formel (a, b, c seien die Gitterkonstanten):
Diese vereinfacht sich beispielsweise für kubische Systeme durch Gleichsetzen von a = b = c weiter:
Herleitungen
Eine Ebene ist eindeutig durch drei nicht auf einer Gerade liegende Punkte definiert. Dies sind hier die Schnittpunkte mit den Kristallachsen:
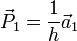 ,
, 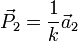 und
und 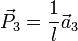 .
.Die Punkte auf der Ebene lassen sich durch die Parameterform
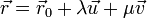 beschreiben (mit Aufpunkt und zwei Richtungsvektoren, die in der Ebene liegen und nicht kollinear sind). Liegen zwei Punkte in der Ebene, so liegt deren Verbindungsvektor ebenfalls in der Ebene. Hierüber lassen sich die Richtungsvektoren konstruieren (
beschreiben (mit Aufpunkt und zwei Richtungsvektoren, die in der Ebene liegen und nicht kollinear sind). Liegen zwei Punkte in der Ebene, so liegt deren Verbindungsvektor ebenfalls in der Ebene. Hierüber lassen sich die Richtungsvektoren konstruieren (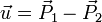 und
und 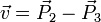 ). Als Aufpunkt wähle irgendeinen in der Ebene liegenden Punkt (hier
). Als Aufpunkt wähle irgendeinen in der Ebene liegenden Punkt (hier 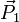 ):
):Bildet man das Skalarprodukt zwischen dem reziproken Gittervektor
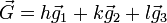 und
und 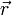 unter Ausnutzung der Relation
unter Ausnutzung der Relation 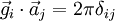 , so ergibt sich:
, so ergibt sich:Für einen Normalenvektor der Ebene
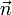 sind die Skalarprodukte mit den Richtungsvektoren gleich Null (
sind die Skalarprodukte mit den Richtungsvektoren gleich Null (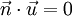 und
und 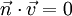 ). Genau das trifft auf
). Genau das trifft auf 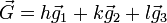 zu, dieser steht also auf der Ebene (hkl) senkrecht.
zu, dieser steht also auf der Ebene (hkl) senkrecht.Durch den Gitterpunkt am Koordinatenursprung verläuft parallel zur gerade betrachteten Ebene durch P1 auch eine Ebene mit den Indizes (hkl). Deren Abstand ist die Projektion eines Verbindungsvektors beider Ebenen (
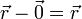 ) auf den normierten Normalenvektor (
) auf den normierten Normalenvektor (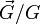 ). Dies ergibt zusammen mit obiger Rechnung den Netzebenenabstand:
). Dies ergibt zusammen mit obiger Rechnung den Netzebenenabstand:Im Nenner treten bei der Betragsbildung sowohl die Längen der reziproken Gittervektoren auf (
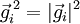 ) als auch die Projektionen der Gittervektoren aufeinander (
) als auch die Projektionen der Gittervektoren aufeinander (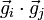 mit
mit 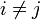 ). Letztere sind bei nicht-orthogonalen Kristallsystemen ungleich Null:
). Letztere sind bei nicht-orthogonalen Kristallsystemen ungleich Null:
Ein orthorhombisches Kristallsystem ist ein rechtwinkliges Kristallsystem mit drei 90°-Winkeln, jedoch ohne gleichlange Achsen. Die Gittervektoren lauten hier ausgedrückt bzgl. der kanonischen Einheitsbasis:Und die dazugehörigen reziproken Gittervektoren sind ebenfalls orthogonal (
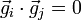 für
für 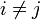 ):
):Setze diese in obige allgemeine Formel für den Netzebenenabstand ein:
Das kubische Kristallsystem ist ebenfalls rechtwinklig, aber zusätzlich sind die Gitterkonstanten bzgl. jeder Kristallachse gleich a = b = c und die Formel vereinfacht sich weiter zu:
Wikimedia Foundation.