- Gleichmäßig stetig
-
Gleichmäßige Stetigkeit ist ein Begriff aus der Analysis. Er bezeichnet einen Spezialfall der Stetigkeit.
Inhaltsverzeichnis
Definition
Sei D eine Teilmenge aus
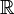 , kurz
, kurz 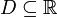 .
.Eine Abbildung
 heißt gleichmäßig stetig genau dann, wenn
heißt gleichmäßig stetig genau dann, wenn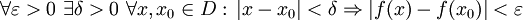 .
.
Zur besseren Unterscheidung bezeichnet man die gewöhnliche Stetigkeit, wenn sie in jedem Punkt von D gegeben ist, auch als punktweise Stetigkeit.
Die Besonderheit der gleichmäßigen Stetigkeit besteht darin, dass δ nur von
 und nicht, wie bei der punktweisen Stetigkeit, noch zusätzlich von der Stelle x0 abhängt.
und nicht, wie bei der punktweisen Stetigkeit, noch zusätzlich von der Stelle x0 abhängt.Anschaulich bedeutet das: Zu jeder noch so kleinen senkrechten Rechteckseite
 kann man eine hinreichend kleine waagrechte Rechteckseite δ finden, sodass, wenn man das Rechteck mit den Seiten
kann man eine hinreichend kleine waagrechte Rechteckseite δ finden, sodass, wenn man das Rechteck mit den Seiten 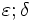 geeignet auf dem Funktionsgraphen entlangführt, dieser immer nur die senkrechten Rechtecksseiten schneidet. (Bsp.: Wurzelfunktion auf
geeignet auf dem Funktionsgraphen entlangführt, dieser immer nur die senkrechten Rechtecksseiten schneidet. (Bsp.: Wurzelfunktion auf 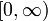 ).
).Beispiele
Betrachte die Funktion
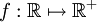 mit f(x) = x2 (s. Abbildung).
mit f(x) = x2 (s. Abbildung).
Diese ist stetig, aber nicht gleichmäßig stetig: Je weiter rechts man zwei Punkte mit einem Abstand kleiner als δ wählt, desto größer wird der Abstand der beiden Funktionswerte. Dies widerspricht der Definition gleichmäßiger Stetigkeit: Unabhängig von den Punkten muss der Abstand der Funktionswerte kleiner als ein vorgegebenes ε sein. Das ist bei dieser Funktion nicht der Fall.
Weiterhin gilt: Jede Einschränkung von f auf ein kompaktes Intervall ist gleichmäßig stetig. Der Beweis lässt sich mit dem Satz von Heine führen.
Ein anderes Beispiel ist die stetige Funktion
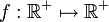 mit
mit 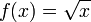
die gleichmäßig stetig, sogar hölderstetig, aber nicht lipschitzstetig ist.
Verallgemeinerung: metrische Räume
Allgemeiner wird auch folgende Definition verwendet:
Seien (X,dx),(Y,dy) zwei metrische Räume. Eine Abbildung
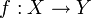 heißt gleichmäßig stetig genau dann, wenn
heißt gleichmäßig stetig genau dann, wenn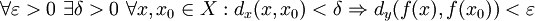 .
.
Verallgemeinerung: uniforme Räume
Noch allgemeiner heißt in der Topologie eine Funktion
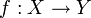 zwischen zwei uniformen Räumen
zwischen zwei uniformen Räumen 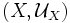 und
und 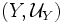 gleichmäßig stetig, wenn das Urbild jeder Nachbarschaft wieder eine Nachbarschaft ist, wenn also
gleichmäßig stetig, wenn das Urbild jeder Nachbarschaft wieder eine Nachbarschaft ist, wenn also 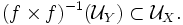
Eigenschaften
Es gilt: Ist f gleichmäßig stetig auf einer Menge M, dann ist f auch stetig in jedem Punkt
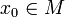 und sogar stetig fortsetzbar auf den Abschluss
und sogar stetig fortsetzbar auf den Abschluss 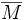 . Umgekehrt gibt es jedoch stetige Funktionen, die nicht gleichmäßig stetig sind.
. Umgekehrt gibt es jedoch stetige Funktionen, die nicht gleichmäßig stetig sind.Ein einfaches Kriterium zum Nachweis gleichmäßiger Stetigkeit ist der Satz von Heine: Jede stetige Funktion auf einer kompakten Menge ist gleichmäßig stetig.
Ist
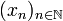 eine Cauchy-Folge im Raum M und ist
eine Cauchy-Folge im Raum M und ist 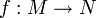 gleichmäßig stetig, so ist auch
gleichmäßig stetig, so ist auch 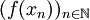 eine Cauchy-Folge in N. Dies gilt im Allgemeinen nicht für Funktionen, die nur stetig sind, wie das Beispiel
eine Cauchy-Folge in N. Dies gilt im Allgemeinen nicht für Funktionen, die nur stetig sind, wie das Beispiel 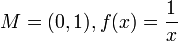 und
und 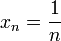 zeigt.
zeigt.Im
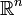 : Polstellen kann es auf einer gleichmäßig stetigen Funktion nicht geben, da bei gegen unendlich strebender Steigung der Abstand der Funktionwerte beliebig groß wird, δ also kein reeller Wert sein kann.
: Polstellen kann es auf einer gleichmäßig stetigen Funktion nicht geben, da bei gegen unendlich strebender Steigung der Abstand der Funktionwerte beliebig groß wird, δ also kein reeller Wert sein kann.Eine spezielle Form der gleichmäßigen Stetigkeit ist die Lipschitz-Stetigkeit.
Sonstiges
- Gleichmäßige Stetigkeit ist nicht zu verwechseln mit gleichmäßiger Konvergenz, die etwas über die Art der Konvergenz von Funktionenfolgen aussagt.
Siehe auch
Wikimedia Foundation.

