Heine-Borel-Eigenschaft

Der Satz von Heine-Borel, auch Überdeckungssatz genannt, nach den Mathematikern Eduard Heine und Émile Borel benannt, ist ein Satz der Topologie metrischer Räume. Er würde besser nach Borel allein benannt; denn Heine hat an ihm keinen Anteil. Von Heine stammt der ebenfalls wichtige Satz, dass jede auf kompaktem Definitionsbereich stetige Funktion gleichmäßig stetig ist.

Er zeigt die Äquivalenz zweier Definitionen der Kompaktheit.

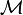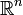Für eine Teilmenge $\mathcal{M}$ des $\mathbb{R}^{n}$ (der metrische Raum aller reellen n-Tupel mit der euklidischen Metrik) sind die folgenden beiden Aussagen äquivalent:

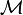1. $\mathcal{M}$ ist beschränkt und abgeschlossen.
2. Jede offene Überdeckung von 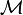$\mathcal{M}$ enthält eine endliche Teilüberdeckung, d.h 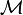$\mathcal{M}$ ist kompakt.

Dieser Satz lässt sich speziell auf Teilmengen der Menge der reellen Zahlen 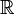$\mathbb{R}$ anwenden.

Gegenbeispiele

Wichtig hierbei ist, dass der umgebende Raum der 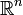$\mathbb{R}^{n}$ ist. Im Allgemeinen ist (Überdeckungs-)Kompaktheit nicht äquivalent zu Abgeschlossenheit und Beschränktheit.

Ein einfaches Gegenbeispiel ist die diskrete Metrik: Sei X eine beliebige Menge. Dann lässt sich immer die sogenannte diskrete Metrik definieren durch

• d(x,x) = 0,
• d(x,y) = 1 für $x\neq y$.

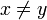In dieser Metrik ist jede Teilmenge abgeschlossen und beschränkt, aber nur die endlichen Teilmengen sind kompakt.

Weitere Gegenbeispiele sind alle unendlich dimensionalen normierten Vektorräume.

Verallgemeinerung

Für allgemeine metrische Räume gilt allerdings, dass die kompakten Mengen diejenigen sind, welche vollständig und totalbeschränkt sind. Dies ist deshalb eine Verallgemeinerung, weil eine Teilmenge des 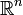$\mathbb{R}^{n}$ genau dann vollständig ist, wenn sie abgeschlossen ist und weil sie genau dann totalbeschränkt ist, wenn sie beschränkt ist.

Siehe auch

• Liste mathematischer Sätze

Weblinks

• Heine Borel (Video, das einen Beweis vom Satz von Heine-Borel illustriert.)