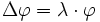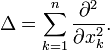- Helmholtz-Differentialgleichung
-
Die Helmholtz-Gleichung (nach Hermann von Helmholtz) ist eine partielle Differentialgleichung. Sie lautet:
in einem Gebiet Ω und geeigneten Randbedingungen auf dem Rand
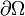 . Dabei ist
. Dabei istder Laplace-Operator in kartesischen Koordinaten.
Die Helmholtz-Gleichung ist dementsprechend eine partielle Differentialgleichung (PDE) zweiter Ordnung aus der Klasse der elliptischen PDE. Sie ergibt sich auch z. B. aus der Wellengleichung nach Trennung der Variablen und Annahme harmonischer Zeitabhängigkeit.
Setzt man λ = 0, so erhält man die Laplace-Gleichung.
Beispiel: Partikuläre Lösung der inhomogenen Maxwellgleichungen
Eine Anwendung aus der Physik ist z. B. die Lösung der inhomogenen Maxwellgleichungen (Maxwellgleichungen mit Strömen und Ladungen). Aus diesen folgt in Gaussschen cgs-Einheiten mit der Lorenz-Eichung:
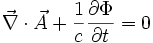
die Gleichung für das elektrische Skalarpotential Φ:
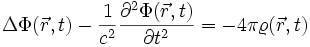
sowie die Gleichung

für das magnetische Vektorpotential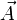 (hier für die einzelnen Komponenten mit:
(hier für die einzelnen Komponenten mit: 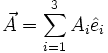 )
)Die allgemeine Lösung dieser Differentialgleichungen ist die Linearkombination der allgemeinen Lösung der dazugehörigen homogenen DGL sowie einer partikulären Lösung der inhomogenen DGL:
Φ = Φhom. + Φpart.
Die Lösung der homogenen DGL sind die elektromagnetischen Wellen; wir beschränken uns hier auf die Herleitung einer partikulären Lösung
Exemplarisch wird nun die Lösung für Φ durchgeführt. Mit hat man dann auch gleichzeitig die Lösungen für
hat man dann auch gleichzeitig die Lösungen für 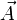 . Wir bilden zunächst die Fourier-Transformierten von Φ und
. Wir bilden zunächst die Fourier-Transformierten von Φ und 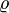
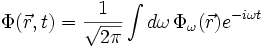
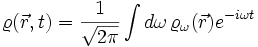
und setzen diese als Ansatz für die Maxwellgleichung
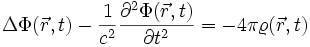 ein:
ein: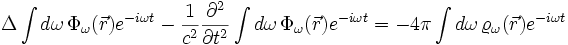
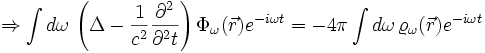
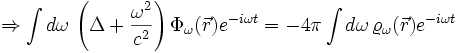
Beide Integranden müssen gleich sein, da sich die dω-Integration über die gleichen Bereiche erstreckt:
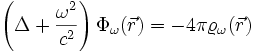
Für
 erkennen wir die Helmholtz-Gleichung wieder.
erkennen wir die Helmholtz-Gleichung wieder.Hier ist k der Betrag des Wellenvektors und heißt Kreiswellenzahl.
 wobei λ die Wellenlänge der elektromagnetischen Welle ist.
wobei λ die Wellenlänge der elektromagnetischen Welle ist.Zur Lösung dieses Problems betrachten wir zunächst

Wir suchen nun also zunächst die Greensche Funktion zum Differentialoperator

Diese lautet:

Dies ist also die Lösung für eine Punktladung am Ort
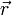 . Damit erhalten wir für die gesamte Ladungsverteilung:
. Damit erhalten wir für die gesamte Ladungsverteilung:
Dieses Ergebnis setzen wir in die Fouriertransformierte für
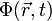 ein und erhalten
ein und erhalten
Wir ersetzen nun
 :
:

Wir setzen nun wieder
 ein:
ein:
Dies ist die gesuchte partikuläre Lösung der inhomogenen Maxwellgleichung. Sie gilt sowohl für Φ als auch für Ai. Damit folgt analog:


Diskussion: Retardierte und avancierte Lösung
Noch steht das Vorzeichen im Argument
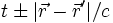 nicht fest. Physikalisch scheint aber plausibel, dass die zeitliche Änderung einer Ladungsverteilung bei
nicht fest. Physikalisch scheint aber plausibel, dass die zeitliche Änderung einer Ladungsverteilung bei 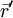 erst zu einem späteren Zeitpunkt bei
erst zu einem späteren Zeitpunkt bei 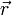 beobachtet werden kann, da sich elektromagnetische Wellen mit der (konstanten) Lichtgeschwindigkeit c ausbreiten. Daher wählen wir das Minuszeichen als physikalisch praktikable Lösung:
beobachtet werden kann, da sich elektromagnetische Wellen mit der (konstanten) Lichtgeschwindigkeit c ausbreiten. Daher wählen wir das Minuszeichen als physikalisch praktikable Lösung: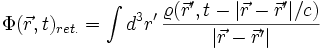
Man nennt das Potential bei Wahl des Minuszeichens auch retardiertes Potential. Wählt man das Pluszeichen, so spricht man vom avancierten Potential.
Weblinks
Wikimedia Foundation.