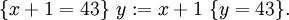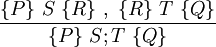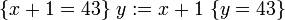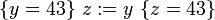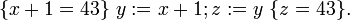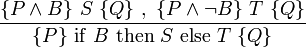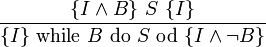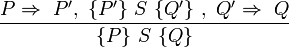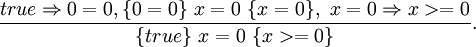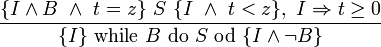- Hoarekalkül
-
Der Hoare-Kalkül (auch Hoare-Logik) ist ein Formales System, entwickelt von dem britischen Informatiker C. A. R. Hoare und später verfeinert von Hoare und anderen Wissenschaftlern. Er wurde 1969 in einem Artikel mit dem Titel An axiomatic basis for computer programming veröffentlicht. Der Zweck des Systems ist es, eine Menge von logischen Regeln zu liefern, die es erlauben, Aussagen über die Korrektheit von imperativen Computer-Programmen zu treffen und sich dabei der mathematischen Logik zu bedienen. Hoare knüpft an frühere Beiträge von Robert Floyd an, der ein ähnliches System für Flussdiagramme veröffentlichte.
Das zentrale Element des Hoare-Kalküls ist das Hoare-Tripel, das beschreibt, wie ein Programmteil den Zustand einer Berechnung verändert:
Dabei nennt man P und Q Zusicherungen (englisch assertions). S ist ein Programmsegment. P heißt die Vorbedingung (englisch precondition), Q heißt die Nachbedingung (englisch postcondition). Zusicherungen sind Formeln der Prädikatenlogik.
Ein Tripel kann auf folgende Weise verstanden werden: Falls P für den Programmzustand vor der Ausführung von S gilt, dann gilt Q danach. Falls S nicht terminiert, dann gibt es kein danach, also kann in diesem Fall Q jede beliebige Aussage sein. Tatsächlich kann man für Q die Aussage false wählen, um auszudrücken, dass S nicht terminiert. Man spricht hier von partieller Korrektheit. Falls S immer terminiert und danach Q wahr ist, spricht man von totaler Korrektheit. Die Terminierung muss unabhängig bewiesen werden.
Inhaltsverzeichnis
Partielle Korrektheit
Der Hoare-Kalkül besteht aus Axiomen und Ableitungsregeln für alle Konstrukte einer einfachen imperativen Programmiersprache:
Zuweisungsaxiom
Das Zuweisungsaxiom besagt, dass nach einer Zuweisung jede Aussage für die Variable gilt, welche vorher für die rechte Seite der Zuweisung galt:
P[x / E] ist die Aussage, die dadurch entsteht, dass man in P jedes freie Vorkommen von x durch E ersetzt.
Genau genommen ist das Zuweisungsaxiom kein einzelnes Axiom, sondern ein Schema für eine unendliche Menge von Axiomen, denn x, E und P können jede mögliche Form annehmen, und P[x / E] kann daraus konstruiert werden.
Ein Beispiel für ein durch das Zuweisungsaxiom beschriebenes Tripel ist:
Kompositionsregel
Diese Regel kann auf folgende Weise angewendet werden: Wenn die über dem Strich stehenden Aussagen bewiesen worden sind, kann die unter dem Strich stehende Aussage auch als bewiesen angesehen werden.
Betrachtet man zum Beispiel die folgenden beiden Aussagen, die aus dem Zuweisungsaxiom folgen
und
kann man die folgende Aussage daraus folgern:
Auswahlregel (if-then-else-Regel)
Die Regel beweist also sowohl den if-Zweig, als auch den else-Zweig.
Iterationsregel (while-Regel)
Hierbei wird I als die Schleifeninvariante bezeichnet.
Konsequenzregel
Die Konsequenzregel erlaubt es, die Vorbedingung zu verstärken und die Nachbedingung abzuschwächen und so die Anwendung anderer Beweisregeln zu ermöglichen. Insbesondere kann man auch die Vor- oder Nachbedingung durch eine äquivalente logische Formel ersetzen. Beispiel:
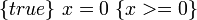 ist partiell korrekt, denn
ist partiell korrekt, denn
Totale Korrektheit
Wie oben erläutert eignet sich das beschriebene Kalkül nur für den Beweis der partiellen Korrektheit. Zum Beweis der totalen Korrektheit kann es durch Erweiterung der while-Regel verwendet werden:
Iterationsregel für totale Korrektheit
Hierbei ist t ein Term, I die Schleifeninvariante – also das, was in jedem Schleifendurchlauf gilt – und z eine Variable, die in B, t, S und I nicht (frei) vorkommt. Sie dient dazu, den Wert des Terms vor der Schleife mit dem nach der Schleife zu vergleichen. Die Bedingung
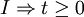 stellt sicher, dass t nicht negativ wird. Die Idee hinter der Regel ist, dass, wenn t mit jedem Schleifendurchlauf abnimmt, aber nie kleiner als Null wird, die Schleife irgendwann enden muss. t muss dabei aus einer fundierten Menge sein.
stellt sicher, dass t nicht negativ wird. Die Idee hinter der Regel ist, dass, wenn t mit jedem Schleifendurchlauf abnimmt, aber nie kleiner als Null wird, die Schleife irgendwann enden muss. t muss dabei aus einer fundierten Menge sein.Literatur
- C. A. R. Hoare: An axiomatic basis for computer programming (pdf). In: Communications of the ACM. 12(10): 576–585, Oktober 1969.
- Robert D. Tennent: Specifying Software. (a recent textbook that includes an introduction to Hoare logic) ISBN 0-521-00401-2 [1]
Weblinks
- Das Project Bali hat Regeln nach Art des Hoare-Kalküls für ein Subset von Java aufgestellt, zur Benutzung mit dem Theorembeweiser Isabelle
- Hoare Tutorial Ein sehr gutes Tutorial das den Umgang mit dem Hoare-Kalkül zur Programmverifikation erklärt
- j-Algo-Modul Hoare Kalkül Ein Visualisierung des Hoare-Kalküls im Rahmen des Algorithmenvisualisierungsprogramms j-Algo
Wikimedia Foundation.

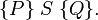
![\{P[x/E]\}\ x:=E \ \{P\}.](/pictures/dewiki/56/864270237efd8757e5926856ac581ca8.png)