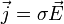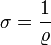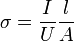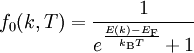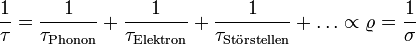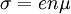- Ionenleitung
-
Die elektrische Leitfähigkeit, auch als Konduktivität bezeichnet, mit dem Formelzeichen σ (griech. sigma) oder auch als κ oder γ, ist eine physikalische Größe, die die Fähigkeit eines Stoffes angibt, elektrischen Strom zu leiten. Die abgeleitete SI-Einheit der elektrischen Leitfähigkeit ist S/m (Siemens pro Meter). Den Kehrwert der elektrischen Leitfähigkeit nennt man spezifischen Widerstand.
Physikalische Größe Name elektrische Leitfähigkeit Größenart Tensor Formelzeichen der Größe σ Größen- und
Einheiten-
systemEinheit Dimension SI 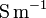
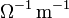
M−1·L−3·T3·I2 Siehe auch: spezifischer Widerstand, elektrischer Leitwert Die elektrische Leitfähigkeit ist definiert als die Proportionalitätskonstante zwischen der Stromdichte
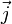 und der elektrischen Feldstärke
und der elektrischen Feldstärke 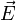 in der allgemeinen Form des ohmschen Gesetzes:
in der allgemeinen Form des ohmschen Gesetzes:Inhaltsverzeichnis
Leitfähigkeit als Tensor
Im speziellen Fall eines homogenen (ortsunabhängigen), isotropen (richtungsunabhängigen) und linearen (feldgrößenunabhängigen) Mediums ist die elektrische Leitfähigkeit ein Skalar (eindimensionaler Wert). Nur in diesem einfachen Fall erfolgt daher die Stromleitung im Leiter proportional und in gleicher Richtung wie das die Stromleitung verursachende elektrische Feld.
Im allgemeinen Fall, wenn eine der obigen Bedingungen nicht zutrifft, ist die elektrische Leitfähigkeit ein Tensor 2. Stufe (Dyade), also ein mehrdimensionaler Wert. Beispiele für Materialien mit solchen Eigenschaften sind Materialien mit Schichtstrukturen wie Graphit und Hochtemperatursupraleiter.
Herkunft und Kehrwert
Es ist zu beachten, dass diese Gleichung – sie zählt zu den drei fundamentalen Materialgleichungen – sich nicht aus den maxwellschen Gleichungen ableiten lässt. Die Maxwellschen Gleichungen mit den Kontinuitätsgesetzen und den Materialgleichungen stellen gemeinsam das Fundament der nicht relativistischen elektrodynamischen Feldtheorie dar.
Der Leitwert ist der Kehrwert des Widerstandes. Der Leitwert eines normiert dimensionierten Stückes eines leitfähigen Materials ist folglich der Kehrwert des spezifischen Widerstands ρ (griech. rho) und wird als dessen spezifischer Leitwert σ bezeichnet (Leitfähigkeit = spezifischer Leitwert). Beide sind über die Formel
verknüpft.
Formelzeichen und Einheiten
Das Formelzeichen für die elektrische Leitfähigkeit ist der griechische Buchstabe σ (sigma). Weitere häufig verwendete Formelzeichen für die elektrische Leitfähigkeit sind κ (kappa) und γ (gamma).
Die abgeleitete SI-Einheit der elektrischen Leitfähigkeit ist S/m (Siemens pro Meter), also A/(V·m). Sehr gebräuchlich sind zudem S/cm, m/(Ω·mm²) und S·m/mm², wobei die Zusammenhänge 1 S/cm = 100 S/m und 1 m/(Ω·mm²) = S·m/mm² = 106 S/m gelten. Eine weitere besonders in den USA gebräuchliche Einheit ist IACS. Hier wird die Leitfähigkeit als Prozentwert der Leitfähigkeit reinen geglühten Kupfers ausgedrückt (sogenannter International Annealed Copper Standard). 100 % IACS entsprechen 58 MS/m.
Messung
Die elektrische Leitfähigkeit kann nicht direkt gemessen werden, sondern wird meist mittels Transportmessungen aus Strom, abfallender Spannung und Probengeometrie analog zum spezifischen Widerstand bestimmt. Je nach Probengeometrie können verschiedene Verfahren verwendet werden: Das Standardverfahren zur Messung einer großflächigen, homogenen Schicht ist die Vierpunktmessung und wird vor allem in der Halbleiterindustrie angewendet. Ist die Schicht dagegen klein und hat eine beliebige Form, kann die Leitfähigkeit mit der Van-der-Pauw-Messmethode bestimmt werden. Für einen langen Leiter bekannten Querschnitts A kann die Leitfähigkeit mittels Vierleitermessung und der Formel
bestimmt werden, wobei I der Strom durch den Leiter und U der Spannungsabfall zwischen zwei im Abstand l befindlichen Kontakten ist.
Ein veraltetes Messgerät zur Messung der elektrischen Leitfähigkeit ist das von Jean-Jacques Rousseau stammende Diagometer.
Elektrische Leitfähigkeit verschiedener Stoffe
Elektrische Leitfähigkeit ausgewählter Materialien bei 300 K Material „Einordnung“ σ in S/m Silber Metall 61,39·106 Kupfer Metall ≥ 58,0·106 [1] Gold Metall 44,0·106[2] Aluminium Metall 36,59·106[2] Natrium Metall 21·106 Wolfram Metall 18,38·106[2] Messing (CuZn37) Metall ≈ 15,5·106 Eisen Metall 10,02·106[2] Chrom Metall 8,74 · 106[2] Blei Metall 4,69·106[2] Titan (bei 273 K) Metall 2,56·106[2] Edelstahl (1.4301) Metall 1,36 · 106 Quecksilber Metall 1,04·106 Gadolinium Metall 0,74·106 Graphit (parallel zu Schichten) Nichtmetall 3 · 106 Diamant Nichtmetall 0,0001 Germanium Halbleiter 1,45 Silizium, undotiert Halbleiter 2,52 · 10−4 Tellur Halbleiter 0,005 Meerwasser – ≈ 5 Leitungswasser – ≈ 0,05 reines Wasser – 5 · 10−6 Nach der elektrischen Leitfähigkeit unterteilt man Stoffe in
- Typischerweise (bei 25 °C): > 106 S/m.
- Die höchste elektrische Leitfähigkeit aller Metalle hat Silber.
- Isolatoren oder Nichtleiter (die meisten Nichtmetalle sowie Kohlenwasserstoffe und viele organische Verbindungen)
- Typischerweise < 10−8 S/m.
- Halbleiter (beispielsweise Silizium, Germanium)
- Bei Halbleitern hängt die Leitfähigkeit von Faktoren, wie Temperatur, Druck oder Belichtung ab. Die Leitfähigkeit liegt im Bereich zwischen Leitern und Isolatoren. Diese Einteilung stammt noch aus der Zeit, als man die Eigenschaften spezieller Halbleiter wie Germanium und Silizium noch nicht kannte. Bei diesen lässt sich die Leitfähigkeit gezielt durch Dotierung (Einlagerung von Fremdatomen) verändern. Diese Stoffgruppe ist vor allem deshalb interessant, weil sich damit spezielle Bauelemente der Elektronik wie z. B. Transistoren herstellen lassen.
- Supraleiter (viele Metalle, verschiedene Legierungen, einige wenige Keramiken und manche Fullerene)
- Unterhalb einer materialabhängigen Sprungtemperatur ist die Leitfähigkeit quasi „unendlich“, der elektrische Widerstand verschwindet vollständig.
- Bei Elektrolytlösungen spricht man von einer elektrolytischen Leitfähigkeit. Hierbei bezieht man die spezifische Leitfähigkeit auf den Widerstand einer Ein-Elektrolytlösung zwischen zwei Elektroden von einem Abstand l = 1 cm und einem Querschnitt von q = 1 cm² , früher bei 18 °C, nach DIN/E-Norm bei 25 °C. Zur auf seine Konzentration bezogenen Leitfähigkeit eines Elektrolyten siehe Molare Leitfähigkeit.
Warum ist ein Stoff elektrisch leitfähig?
Die Leitfähigkeit eines Stoffes oder Stoffgemisches hängt von der Verfügbarkeit von beweglichen Ladungsträgern ab. Dies können locker gebundene Elektronen, wie beispielsweise in Metallen, aber auch Ionen oder delokalisierte Elektronen in organischen Molekülen sein. Letztere werden häufig durch mesomere Grenzstrukturen beschrieben.
Wässrige Lösungen zeichnen sich durch eine geringe Leitfähigkeit aus. Sie steigt, wenn dem Wasser Ionen, also Salze, Säuren oder Basen hinzugefügt werden. Dementsprechend hat Meerwasser eine höhere elektrische Leitfähigkeit als Süßwasser. Reines Wasser (destilliertes oder demineralisiertes) hat eine äußerst geringe Leitfähigkeit und wird gelegentlich bereits als Nichtleiter bezeichnet.
In Halbleitern nutzt man gezielte Verunreinigungen, um die Leitfähigkeit zu beeinflussen (Dotierung). Durch Elektronendonatoren (Elemente mit mehr Außenelektronen als das Material) werden sie n-dotiert, durch Elektronenakzeptoren (Elemente mit weniger Elektronen als das Material) p-dotiert. Durch die p-Dotierung entstehen Elektronenfehlstellen, auch Löcher genannt, die ebenso zur Leitung des elektrischen Stroms beitragen und die Leitfähigkeit ähnlich erhöhen wie überzählige Elektronen in n-dotierten Halbleitern.
Ein Modell zur Veranschaulichung und Erklärung der Leitfähigkeit eines Kristalls ist durch das Bändermodell gegeben.
Da die thermische Leitfähigkeit in metallischen Festkörpern vor allem durch die Elektronen bestimmt wird, sind elektrische und thermische Leitfähigkeit durch das Wiedemann-Franzsche Gesetz verknüpft.
Ursache des elektrischen Widerstandes
1900 formulierte Paul Drude ein nach ihm benanntes Modell, wonach der elektrische Widerstand durch Kollision der Leitungselektronen mit den als starr angenommenen Atomrümpfen des Metalls verursacht wird. Danach ist die Leitfähigkeit
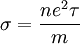 .
.
Hier ist n die Konzentration freier Elektronen, e die Ladung, m die Masse eines Elektrons und τ die mittlere Flugzeit des Elektrons zwischen zwei Stößen (Relaxationszeit). Dieses Modell veranschaulicht die elektrische Leitfähigkeit zwar recht gut, sagt aber manche experimentellen Ergebnisse falsch voraus, da die Annahme des freien Elektronengases zu ungenau ist: Elektronen sind Fermionen, das heißt, jeder Energiezustand im reziproken k-Raum
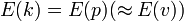 kann nur von zwei Elektronen eingenommen werden, sodass selbst am absoluten Nullpunkt Energieniveaus bis zur Fermi-Energie EF besetzt sind und die Fermi-Kugel bilden. Die temperaturabhängige Wahrscheinlichkeit, ob die Energie E(k) mit Elektronen besetzt ist, wird dabei durch die Fermi-Dirac-Verteilung
kann nur von zwei Elektronen eingenommen werden, sodass selbst am absoluten Nullpunkt Energieniveaus bis zur Fermi-Energie EF besetzt sind und die Fermi-Kugel bilden. Die temperaturabhängige Wahrscheinlichkeit, ob die Energie E(k) mit Elektronen besetzt ist, wird dabei durch die Fermi-Dirac-Verteilunggegeben. Da die Fermi-Energie EF mit einigen Elektronenvolt wesentlich größer als die thermische Energie kBT mit einigen dutzend Millielektronenvolt ist, sind nur Elektronen nahe der Fermi-Energie angeregt und tragen zur elektrischen Leitfähigkeit bei. Im Nicht-Gleichgewichtszustand wird die Zeitabhängigkeit der Verteilung durch die Boltzmann-Gleichung beschrieben. Mit dieser Verbesserung, der Sommerfeld-Theorie, folgt schließlich die gleiche Leitfähigkeit wie nach Drude, jedoch mit zwei entscheidenden Veränderungen:
- Die Relaxationszeit τ ist die Relaxationszeit der Elektronen an der Fermikante, also die der Elektronen mit der Energie EF.
- Die Masse der Elektronen m hat im Kristall scheinbar eine abweichende, effektive Masse m * , welche richtungsabängig und somit auch eine tensorielle Größe ist.
Der Reziprokwert der Relaxationzeit, die Streurate (Anzahl von Streuungen pro Zeit), ist dabei die Summe der individuellen Streuraten der Elektronen an Schwingungen der Atomrümpfe (den Phononen), an anderen Elektronen, an Gitterfehlern (Fremdatome, Fehlstellen, etc.) im Kristall oder auch den Wänden des Kristalls. Daraus ergibt sich eine Verallgemeinerung der Matthiessenschen Regel:
Die individuellen Relaxationszeiten führen zu den verschiedenen Temperaturabängigkeiten der Leitfähigkeit im Metall. So ist z. B. die Streuung an Störstellen temperaturunabhängig und führt zum Restwiderstand, wohingegen die Elektron-Phonon-Streuung bei Zimmertemperatur proportional zur Temperatur ist.
Wenn man in einem allgemeinen Festkörper die Beweglichkeit μ der Ladungsträger berücksichtigt, ergibt sich:
wobei n die Ladungsträgerdichte (Anzahl je Volumeneinheit) ausdrückt.
Temperaturabhängigkeit
Damit lassen sich gut die Temperaturabhängigkeiten der Leitfähigkeit erklären:
Metalle
In Metallen ist n konstant, aber die Beweglichkeit nimmt mit steigender Temperatur ab wegen zunehmender Stöße mit den Atomen bzw. wegen dadurch sinkendem τ. Also sinkt auch die Leitfähigkeit.
Beispiel: Eine elektrische Glühlampe ist im ausgeschalteten Zustand kalt und damit gut leitfähig. Im Augenblick des Einschaltens fließt zunächst ein hoher Einschaltstrom, der bis zu zehnmal größer sein kann als der spätere Betriebsstrom. Dadurch wird die Glühwendel erhitzt, erhöht ihren Widerstand und der Strom sinkt auf das Normalniveau. Grobe Faustregel: Pro Grad Temperaturerhöhung steigt der Widerstand um 1/273 seines Wertes. Glühlampen werden manchmal (statt zur Lichterzeugung) zur Strombegrenzung in elektronischen Schaltungen verwendet, z. B. in Lautsprecherverstärkern.
undotierte Halbleiter
In Halbleitern nimmt die Beweglichkeit zwar aus demselben Grund ab, aber die Ladungsträgerdichte steigt überproportional (genauer: exponentiell) durch Anregung ins Leitungsband, so dass die Leitfähigkeit mit der Temperatur stark steigt. Eine praktische Anwendung der Temperaturabhängigkeit ist die Temperaturmessung mit Hilfe einer stromdurchflossenen Diode, ihr Durchgangswiderstand reagiert sehr empfindlich auf kleine Temperaturänderungen.
Einzelnachweise
- ↑ bei 99,9 % Cu, ≥ 58,6 bei 99,99 % Cu, Info der Norddeutschen Affinerie
- ↑ a b c d e f g David R. Lide: CRC Handbook of Chemistry and Physics: 87th Edition: 2006 - 2007. 87th ed. Auflage. B&T, 2006, ISBN 0849304873.
Literatur
Neil W. Ashcroft, N. David Mermin: Solid State Physics. Saunders College Publishing, New York 1976, ISBN 0-03-083993-9.
Weblinks
Wikimedia Foundation.