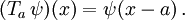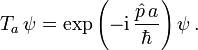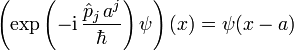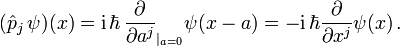- Kanonische Vertauschungsrelationen
-
Der Impulsoperator gehört in der Quantenmechanik zur Impulsmessung von Teilchen.
Der physikalische Zustand
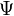 eines Teilchens ist in der Quantenmechanik mathematisch durch einen zugehörigen Vektor eines Hilbertraumes H gegeben. Dieser Zustand wird folglich in der Bra-Ket-Notation durch den Vektor
eines Teilchens ist in der Quantenmechanik mathematisch durch einen zugehörigen Vektor eines Hilbertraumes H gegeben. Dieser Zustand wird folglich in der Bra-Ket-Notation durch den Vektor 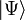 beschrieben. Die Observablen werden durch selbstadjungierte Operatoren auf H dargestellt. Speziell ist der Impuls-Operator die Zusammenfassung der drei Observablen
beschrieben. Die Observablen werden durch selbstadjungierte Operatoren auf H dargestellt. Speziell ist der Impuls-Operator die Zusammenfassung der drei Observablen 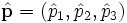 , so dass
, so dassder Mittelwert (Erwartungswert) der Meßergebnisse der j-ten Komponente des Impulses des Teilchens im Zustand
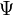 ist.
ist.Definition und Eigenschaften
- Bei der kanonischen Quantisierung deutet man die Phasenraumkoordinaten, den Ort x und den Impuls p des klassischen Systems als selbstadjungierte Operatoren eines Hilbertraums und fordert für die Ortsoperatoren und Impulsoperatoren die kanonischen Vertauschungsrelationen
-
- in Analogie zu den Poisson-Klammern der Hamiltonschen Formulierung
- Der Faktor
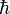 ist aus Dimensionsgründen erforderlich, denn Ort mal Impuls hat die Dimension eines Drehimpulses oder einer Wirkung. Die imaginäre Einheit i muss auftreten, da
ist aus Dimensionsgründen erforderlich, denn Ort mal Impuls hat die Dimension eines Drehimpulses oder einer Wirkung. Die imaginäre Einheit i muss auftreten, da 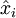 und
und 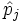 selbstadjungiert sind und ihr Kommutator daher bei Adjunktion sein Vorzeichen wechselt.
selbstadjungiert sind und ihr Kommutator daher bei Adjunktion sein Vorzeichen wechselt.
- Aus den kanonischen Vertauschungsrelationen folgt, dass die drei Komponenten des Impulses gemeinsam messbar sind und dass ihr Spektrum (Bereich der möglichen Messwerte) aus dem gesamten Raum
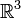 besteht. Die möglichen Impulse sind also nicht quantisiert, sondern kontinuierlich.
besteht. Die möglichen Impulse sind also nicht quantisiert, sondern kontinuierlich. - Die Ortsdarstellung ist durch die Spektraldarstellung des Ortsoperators definiert. Der Hilbertraum H ist der Raum der quadratintegrierbaren, komplexen Funktionen des Ortsraums
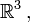 jeder Zustand Ψ ist durch eine Ortswellenfunktion
jeder Zustand Ψ ist durch eine Ortswellenfunktion 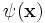 gegeben. Die Ortsoperatoren
gegeben. Die Ortsoperatoren 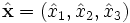 sind die Multiplikationsoperatoren mit den Koordinatenfunktionen, das heißt, der Ortsoperator
sind die Multiplikationsoperatoren mit den Koordinatenfunktionen, das heißt, der Ortsoperator 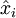 wirkt auf Ortswellenfunktionen durch die Multiplikation der Wellenfunktion mit der Koordinatenfunktion xi
wirkt auf Ortswellenfunktionen durch die Multiplikation der Wellenfunktion mit der Koordinatenfunktion xi
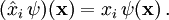
- Der mathematische Satz von Stone und von Neumann besagt dann, dass dann (bei geeigneter Wahl von Phasen) der Impulsoperator, der in den kanonischen Vertauschungsrelationen auftritt, auf Ortswellenfunktionen als Differentialoperator wirkt:
-
- Sein Erwartungswert ist
- In der Impulsdarstellung wirkt der Impulsoperator multiplikativ auf quadratintegrierbare Impulswellenfunktionen
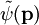
-
- und der Ortsoperator wirkt als Differentialoperator
- Die Orts- und Impulsoperatoren sind Linearkombinationen von Erzeugungs- und Vernichtungsoperatoren:
-
- Dabei sind l1,l2,l3 frei wählbare Längen (größer Null) und die Erzeugungs- und Vernichtungsoperatoren genügen den Vertauschungsrelationen
Warum ist der Impulsoperator ein Differentialoperator?
Nach dem Noether-Theorem gehört zu jeder kontinuierlichen Symmetrie der Wirkung eine Erhaltungsgröße und umgekehrt. Beispielsweise ist der Impuls genau dann erhalten, wenn die Wirkung translationsinvariant ist. In der Hamiltonschen Formulierung erzeugt die Erhaltungsgröße die Symmetrietransformation im Phasenraum durch ihre Poisson-Klammer, der Impuls erzeugt Verschiebungen.
Auf eine Wellenfunktion ψ angewendet ergibt jede Verschiebung um a die verschobene Funktion
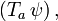 die an jeder Stelle x den Wert hat, den ψ am Urbild x − a hatte,
die an jeder Stelle x den Wert hat, den ψ am Urbild x − a hatte,Die Erzeugende dieser einparametrigen Schar von Verschiebungen definiert bis auf einen Faktor
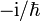 den Impuls, das heißt, der Impuls
den Impuls, das heißt, der Impuls 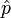 erfüllt definitionsgemäß
erfüllt definitionsgemäßDabei tritt der Faktor
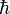 aus Dimensionsgründen auf, denn das Produkt von Impuls und Ort hat die Dimension eines Drehimpulses oder einer Wirkung. Die imaginäre Einheit i ist erforderlich, da Ta eine unitäre Transformation ist und der Impuls selbstadjungiert sein soll. Leitet man die Gleichung
aus Dimensionsgründen auf, denn das Produkt von Impuls und Ort hat die Dimension eines Drehimpulses oder einer Wirkung. Die imaginäre Einheit i ist erforderlich, da Ta eine unitäre Transformation ist und der Impuls selbstadjungiert sein soll. Leitet man die Gleichungnach aj bei a = 0 ab, so ergibt sich der Impulsoperator als Ableitung nach dem Ort,
Siehe auch
Wikimedia Foundation.

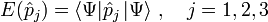
![[\hat{x}_i,\hat{p}_j] = \mathrm{i}\,\hbar\,\delta_{ij}\ ,\quad
[\hat{x}_i,\hat{x}_j]= 0 = [\hat{p}_i,\hat{p}_j]\ ,\quad i,j\in \{1,2,3\}](/pictures/dewiki/50/283b28f1bb85ac377b5281155df03e0b.png)
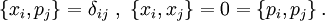
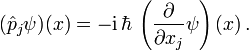
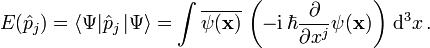
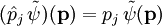
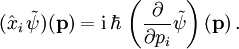
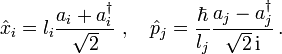
![[a_i, a_j] = 0 = [a_i^\dagger, a_j^\dagger]\ ,\quad [a_i, a^\dagger_j] = \delta_{ij}\ ,\quad i,j\in\{1,2,3\}\,.](/pictures/dewiki/97/aad1861afdc063c859d8f982b226e0af.png)