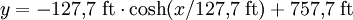- Kettenkurve
-
Eine Katenoide (auch Kettenlinie oder Kettenkurve, englisch catenary oder funicular curve) ist eine mathematische Kurve, die den Durchhang einer an ihren Enden aufgehängten Kette unter Einfluss der Schwerkraft beschreibt. Es handelt sich um eine elementare mathematische Funktion, den Cosinus Hyperbolicus, kurz cosh.
Inhaltsverzeichnis
Mathematische Beschreibung
Die Berechnung der Kettenlinie ist ein klassisches Problem der Variationsrechnung. Zu minimieren ist die potentielle Energie der gesamten Kette unter den Nebenbedingungen, dass die Kettenlänge und die Aufhängepunkte vorgegeben sind. Die Kettenkurve ist die Lösung der Differentialgleichung:
Die Gleichung folgt aus der Überlegung, dass die Masse sich gleichmäßig über die Kette verteilt und keine Biegemomente auftreten:
- FZug = FGewicht



Die Lösungen der Gleichung sind vom Typ
a ist eine Konstante, vx die Verschiebung in x-Richtung, vy die Verschiebung in y-Richtung und cosh der Cosinus Hyperbolicus. Dabei ist a der Krümmungsradius im Scheitelpunkt (siehe Abbildung). Die Kurve hat also stets dieselbe Gestalt, sie ist eine um den Maßstab a vergrößerte Cosinus-Hyperbolicus-Funktion
Die Länge L der Kettenkurve zwischen zwei Punkten 0 und W beträgt mit a = m / k und vx = W / 2 (siehe Kurvenintegral):
Des Weiteren gelten die Beziehungen
wobei h der "Durchhang" ist.
Die potentielle Energie dieses Systems beträgt
wobei μ die Masse je Meter (die Gesamtmasse also
 ) und g die Schwerebeschleunigung ist. Genauer ist dies die Energiedifferenz zwischen einem durchhängenden Seil und einem Seil, das sich komplett auf der Höhe der Aufhängepunkte (y = 0) befindet.
) und g die Schwerebeschleunigung ist. Genauer ist dies die Energiedifferenz zwischen einem durchhängenden Seil und einem Seil, das sich komplett auf der Höhe der Aufhängepunkte (y = 0) befindet.Beziehungen zu anderen Funktionen
Parabel
Erst Gottfried Leibniz, Christiaan Huygens und Johann Bernoulli wiesen 1691 nach, dass sich die Kettenkurve von einer Parabel unterscheidet. Die Parabel stellt sich ein bei einer gleichmäßig über die Spannweite x verteilten Streckenlast, z.B. einer Hängebrücke, bei der das Gewicht der Seile gegenüber dem der Fahrbahn vernachlässigt werden kann. Die Abbildung rechts vergleicht den Kurvenverlauf einer Kettenlinie (rot) mit einer Normalparabel (blau). Bei gleicher Höhe ist die Parabel kürzer, die Kettenkurve dafür weniger gekrümmt.
Katenoid
Die durch Rotation der Katenoide um die x-Achse erzeugte Rotationsfläche wird als Katenoid bezeichnet und ist eine Minimalfläche.
Traktrix
Die Katenoide ist die Evolute zu der Traktrix (Schleppkurve).
Beispiele
Für a = 100 m und einen Mastabstand w von 200 m (also Spezialfall w / 2 = a) wird ein 2·117,5 m langes Seil benötigt:
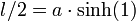 . Der Durchhang beträgt 54 m. Für ein Stahlseil mit 100 cm2 Querschnitt wiegt eine Seilhälfte 9,2 t. Die entsprechende Gewichtskraft von 9·104 N ist die vertikale Kraft an einer Aufhängung. Die horizontale Kraft an einer Aufhängung beträgt 7,7·104 N.
. Der Durchhang beträgt 54 m. Für ein Stahlseil mit 100 cm2 Querschnitt wiegt eine Seilhälfte 9,2 t. Die entsprechende Gewichtskraft von 9·104 N ist die vertikale Kraft an einer Aufhängung. Die horizontale Kraft an einer Aufhängung beträgt 7,7·104 N.Beträgt a etwa 20,2 % der gesamten Breite w, so ist der Durchhang y(x = w / 2) gleich der Breite w (quadratförmige Gesamtabmessungen). Dieser Fall liegt beispielsweise vor beim Gateway Arch (siehe unten im Abschnitt Architektur), der 630 Fuß breit und ebenso hoch ist. Die exakte Formel
mit a = 127,7 Fuß und w/2 = 315 Fuß ist im Inneren des Denkmals ausgestellt.
Anwendungen in der Architektur
Einer der Kettenlinie ähnlichen Stützlinie folgt der scherkräftefreie Bogen des 192 m hohen Gateway Arch in St. Louis. Durch die unterschiedliche Stärke des Bogens liegt jedoch keine echte Katenoide vor.
Siehe auch
Weblinks
Wikimedia Foundation.