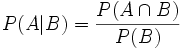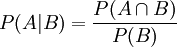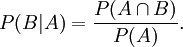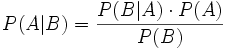- Kolmogorov-Axiome
-
Die Wahrscheinlichkeitstheorie oder Wahrscheinlichkeitsrechnung ist ein Teilgebiet der Mathematik. Gemeinsam mit der Kombinatorik und der mathematischen Statistik bildet sie das mathematische Teilgebiet der Stochastik, die von der Beschreibung zufälliger Ereignisse und ihrer Modellierung handelt.
Inhaltsverzeichnis
Axiomatischer Aufbau
Wie jedes Teilgebiet der modernen Mathematik wird auch die Wahrscheinlichkeitstheorie mengentheoretisch formuliert und auf axiomatischen Vorgaben aufgebaut. Ausgangspunkt der Wahrscheinlichkeitstheorie sind Ereignisse, die als Mengen aufgefasst werden und denen Wahrscheinlichkeiten zugeordnet sind; Wahrscheinlichkeiten sind reelle Zahlen zwischen 0 und 1; die Zuordnung von Wahrscheinlichkeiten zu Ereignissen muss gewissen Mindestanforderungen genügen.
Diese Definitionen geben keinen Hinweis darauf, wie man die Wahrscheinlichkeiten einzelner Ereignisse ermitteln kann; sie sagen auch nichts darüber aus, was Zufall und was Wahrscheinlichkeit eigentlich sind. Die mathematische Formulierung der Wahrscheinlichkeitstheorie ist somit für verschiedene Interpretationen offen, ihre Ergebnisse sind dennoch exakt und vom jeweiligen Verständnis des Wahrscheinlichkeitsbegriffs unabhängig.
Definitionen
Konzeptionell wird als Grundlage der mathematischen Betrachtung von einem Zufallsvorgang oder Zufallsexperiment ausgegangen. Alle möglichen Ergebnisse dieses Zufallsvorgangs fasst man in der Ergebnismenge Ω zusammen. Wenn ein bestimmtes Ergebnis eintritt, spricht man von einem Ereignis. Das Ereignis ist als Teilmenge von Ω definiert. Umfasst das Ereignis genau ein Element der Ergebnismenge, handelt es sich um ein Elementarereignis. Zusammengesetzte Ereignisse enthalten mehrere Ergebnisse. Das Ergebnis ist also ein Element der Ergebnismenge, das Ereignis jedoch eine Teilmenge, wobei diese Unterscheidung häufig vernachlässigt wird.
Damit man den Ereignissen in sinnvoller Weise Wahrscheinlichkeiten zuordnen kann, werden sie in einem Mengensystem aufgeführt, der Ereignisalgebra oder dem Ereignisraum Σ, einer Menge von Teilmengen von Ω. Die Wahrscheinlichkeiten sind dann Bilder einer gewissen Abbildung P des Ereignisraums in das Intervall [0,1]. Solch eine Abbildung heißt Wahrscheinlichkeitsmaß, was definiert ist als ein Maß P: Σ →[0,1] im Sinne der Maßtheorie mit P(Ω)=1. Das Tripel (Ω, Σ, P) wird als Wahrscheinlichkeitsraum bezeichnet.
Im weiteren ist zwischen abzählbaren und überabzählbaren Ergebnismengen zu unterscheiden.
Abzählbare Ergebnismenge
Beispiel: Ein Glücksrad mit Ergebnismenge Ω={1,2,3}, Ereignisraum Σ (hier die Potenzmenge von Ω) und Wahrscheinlichkeitsmaß P.Bei einer abzählbaren Ergebnismenge kann jedem Elementarereignis eine positive Wahrscheinlichkeit zugewiesen werden. Wenn Ω endlich oder abzählbar unendlich ist, kann man für die σ-Algebra Σ die Potenzmenge von Ω wählen. Die Summe der Wahrscheinlichkeiten aller Elementarereignisse aus Ω ist hier 1.
Überabzählbare Ergebnismenge
Die Wahrscheinlichkeit, mit einer als punktförmig angenommenen Dartspitze einen bestimmten Punkt auf einer Scheibe zu treffen, ist null. Eine sinnvolle mathematische Theorie kann man nur auf der Wahrscheinlichkeit aufbauen, bestimmte Gebiete zu treffen. Wenn man diese Gebiete wiederum als infinitesimal annimmt, gelangt man zum Begriff der Wahrscheinlichkeitsdichte.Ein Prototyp einer überabzählbaren Ergebnismenge ist die Menge der reellen Zahlen. In vielen Modellen ist es nicht möglich, allen Teilmengen der reellen Zahlen sinnvoll eine Wahrscheinlichkeit zuzuordnen. Als Ereignissystem wählt man statt der Potenzmenge der reellen Zahlen hier meist die Borelsche σ-Algebra, das ist die kleinste σ-Algebra, die alle Intervalle von reellen Zahlen als Elemente enthält. Die Elemente dieser σ-Algebra nennt man Borelsche Mengen oder auch (Borel)-messbar. Wenn die Wahrscheinlichkeit P(A) jeder Borelschen Menge A als Integral
über eine Wahrscheinlichkeitsdichte f geschrieben werden kann, wird P absolut stetig genannt. In diesem Fall (aber nicht nur in diesem) haben alle Elementarereignisse {x} die Wahrscheinlichkeit 0. Die Wahrscheinlichkeitsdichte eines absolut stetigen Wahrscheinlichkeitsmaßes P ist nur fast überall eindeutig bestimmt, d. h. sie kann auf einer beliebigen Lebesgue-Nullmenge, also einer Menge vom Lebesgue-Maß 0, abgeändert werden, ohne dass P verändert wird. Wenn die erste Ableitung der Verteilungsfunktion von P existiert, so ist sie eine Wahrscheinlichkeitsdichte von P. Die Werte der Wahrscheinlichkeitsdichte werden jedoch nicht als Wahrscheinlichkeiten interpretiert.
Im Rahmen eines maßtheoretischen Aufbaus der Wahrscheinlichkeitstheorie wird der Begriff der Wahrscheinlichkeitsdichte verallgemeinert zum Begriff der Dichte eines Wahrscheinlichkeitsmaßes relativ zu einem Referenzmaß. Im oben beschriebenen Fall ist das Referenzmaß gleich dem Borel-Lebesgue-Maß.
Axiome von Kolmogorow
Die axiomatische Begründung der Wahrscheinlichkeitstheorie wurde in den 1930er Jahren von Andrei Kolmogorow entwickelt. Ein Wahrscheinlichkeitsmaß muss demnach die folgenden drei Kolmogorow-Axiome erfüllen:
- Für jedes Ereignis A aus Σ ist die Wahrscheinlichkeit eine reelle Zahl zwischen 0 und 1: 0≤P(A)≤1.
- Das sichere Ereignis hat die Wahrscheinlichkeit 1: P(Ω)=1.
- Die Wahrscheinlichkeit einer Vereinigung abzählbar vieler inkompatibler Ereignisse entspricht der Summe der Wahrscheinlichkeiten der einzelnen Ereignisse. Inkompatible Ereignisse sind paarweise disjunkte Mengen A1, A2 …; es muss also gelten:
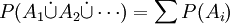 . Diese Eigenschaft wird auch σ-Additivität genannt.
. Diese Eigenschaft wird auch σ-Additivität genannt.
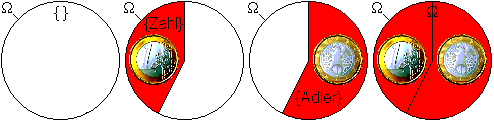
Beispiel: Die Ereignisse beim Werfen einer Münze mögen Zahl oder Adler lauten.
- Dann ist die Ergebnismenge Ω={Zahl, Adler}.
- Als Ereignisraum kann die Potenzmenge
 gewählt werden, also
gewählt werden, also 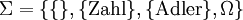 .
. - Für das Wahrscheinlichkeitsmaß P steht aufgrund der Axiome fest:
- P({}) = 0;
- P({Zahl}) = 1 − P({Adler});
- P(Ω) = 1.
Ergebnismenge und Teilmengen bei einem (nicht idealen) MünzwurfZusätzliches (außermathematisches) Wissen ist erforderlich, um P({Zahl}) = P({Adler}) = 0,5 anzusetzen. Dies kann ja durchaus von der Beschaffenheit der Münze abhängen. (siehe A-priori-Wahrscheinlichkeit)
Folgerungen
Aus den Axiomen ergeben sich unmittelbar einige Folgerungen:
1. Aus der Additivität der Wahrscheinlichkeit disjunkter Ereignisse folgt, dass komplementäre Ereignisse (Gegenereignisse) komplementäre Wahrscheinlichkeiten (Gegenwahrscheinlichkeiten) haben: P(Ω\A) = 1-P(A).
- Beweis: Es ist
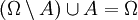 sowie
sowie 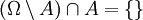 . Folglich nach Axiom (3):
. Folglich nach Axiom (3): 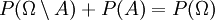 und dann nach Axiom (2):
und dann nach Axiom (2): 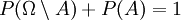 . Umgestellt ergibt sich:
. Umgestellt ergibt sich: 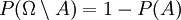 .
.
2. Daraus folgt, dass das unmögliche Ereignis, die leere Menge, die Wahrscheinlichkeit Null hat: P({})=0.
- Beweis: Es ist
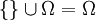 und
und 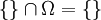 , also nach Axiom (3): P({}) + P(Ω) = P(Ω), d. h. nach Axiom (2): P({}) + 1 = 1. Hieraus folgt P({}) = 0.
, also nach Axiom (3): P({}) + P(Ω) = P(Ω), d. h. nach Axiom (2): P({}) + 1 = 1. Hieraus folgt P({}) = 0.
3. Für die Vereinigung nicht notwendig disjunkter Ereignisse folgt:
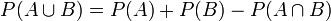 .
.- Beweis: Die für den Beweis erforderlichen Mengen sind im obigen Bild dargestellt. Die Menge
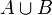 kann danach als Vereinigung von drei disjunkten Mengen dargestellt werden:
kann danach als Vereinigung von drei disjunkten Mengen dargestellt werden:
- Hieraus folgt nach (3):
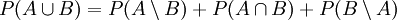 .
. - Andererseits ist nach (3) sowohl
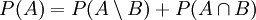 als auch
als auch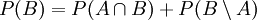 .
.- Addition liefert:
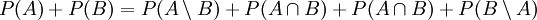
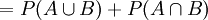 .
.- Umstellen ergibt
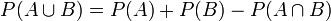 .
.
- Die Siebformel von Poincaré-Sylvester verallgemeinert diese Behauptung im Falle n verschiedener (nicht notwendig disjunkter) Teilmengen.
Spezielle Eigenschaften im Fall diskreter Wahrscheinlichkeitsräume
Laplace-Experimente
Wenn man annimmt, dass nur endlich viele Elementarereignisse möglich und alle gleichberechtigt sind, d. h. mit der gleichen Wahrscheinlichkeit eintreten (wie zum Beispiel beim Werfen einer idealen Münze, wo {Zahl} und {Adler} jeweils die Wahrscheinlichkeit 0,5 besitzen), so spricht man von einem Laplace-Experiment. Dann lassen sich Wahrscheinlichkeiten einfach berechnen: Wir nehmen eine endliche Ergebnismenge Ω an, die die Mächtigkeit |Ω| = n besitzt, d. h. sie hat n Elemente. Dann ist die Wahrscheinlichkeit jedes Elementarereignisses einfach
 .
.- Beweis: Wenn |Ω| = n ist, dann gibt es n Elementarereignisse E1 bis En. Es ist dann einerseits
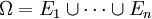 und andererseits sind je zwei Elementarereignisse disjunkt (inkompatibel: wenn das eine eintritt, kann das andere nicht eintreten). Also sind die Voraussetzungen für Axiom (3) erfüllt, und es gilt:
und andererseits sind je zwei Elementarereignisse disjunkt (inkompatibel: wenn das eine eintritt, kann das andere nicht eintreten). Also sind die Voraussetzungen für Axiom (3) erfüllt, und es gilt:  .
.- Da nun andererseits
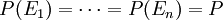 sein soll, ist
sein soll, ist 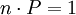 und daher umgestellt:
und daher umgestellt:  wie behauptet.
wie behauptet.
Als Konsequenz folgt, dass für Ereignisse, die sich aus mehreren Elementarereignissen zusammensetzen, die entsprechend vielfache Wahrscheinlichkeit gilt. Ist A ein Ereignis der Mächtigkeit |A| = m, so ist A die Vereinigung von m Elementarereignissen. Jedes davon hat die Wahrscheinlichkeit
 , also ist
, also ist 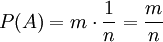 . Man erhält also den einfachen Zusammenhang:
. Man erhält also den einfachen Zusammenhang: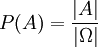 .
.
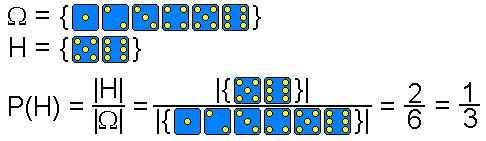
Bei Laplace-Versuchen ist die Wahrscheinlichkeit eines Ereignisses gleich der Zahl der für dieses Ereignis günstigen Ergebnisse, dividiert durch die Zahl der insgesamt möglichen Ergebnisse.
Das nachstehende Bild zeigt ein Beispiel beim Würfeln mit einem idealen Würfel.
Das Ereignis H = Hohe Augenzahl (5 oder 6) hat die Wahrscheinlichkeit 1/3.Ein typischer Laplace-Versuch ist auch das Ziehen einer Karte aus einem Spiel mit n Karten oder das Ziehen einer Kugel aus einer Urne mit n Kugeln. Hier hat jedes Elementarereignis die gleiche Wahrscheinlichkeit.
Das Konzept der Laplace-Experimente lässt sich auf den Fall einer stetigen Gleichverteilung verallgemeinern.
Bedingte Wahrscheinlichkeit
Unter einer bedingten Wahrscheinlichkeit versteht man die Wahrscheinlichkeit für das Eintreten eines Ereignisses A unter der Voraussetzung, dass das Eintreten eines anderen Ereignisses B bereits bekannt ist. Natürlich muss B eintreten können, es darf also nicht das unmögliche Ereignis sein. Man schreibt dann P(A|B) oder seltener PB(A) für „Wahrscheinlichkeit von A unter der Voraussetzung B“, kurz „P von A, vorausgesetzt B“.
Beispiel: Die Wahrscheinlichkeit, aus einem Skatblatt eine Herz-Karte zu ziehen (Ereignis A), beträgt 1/4, denn es gibt 32 Karten und darunter 8 Herz-Karten. Dann ist P(„Herz“) = 8/32 = 1/4.
Ergebnismenge beim Ziehen einer Karte aus einem SkatspielWenn nun aber bereits das Ereignis B „Die Karte ist rot“ eingetreten ist (es wurde eine Herz- oder Karo-Karte gezogen, es ist aber nicht bekannt, welche der beiden Farben), man also nur noch die Auswahl unter den 16 roten Karten hat, dann ist P(A|B) = 8/16 = 1/2 die Wahrscheinlichkeit, dass es sich dann um das Herz-Blatt handelt.
Diese Überlegung galt für einen Laplaceversuch. Für den allgemeinen Fall definiert man die bedingte Wahrscheinlichkeit von „A, vorausgesetzt B“ als
Dass diese Definition sinnvoll ist, zeigt sich daran, dass die so definierte Wahrscheinlichkeit den Axiomen vom Kolmogorow genügt, wenn man sich auf B als neue Ergebnismenge beschränkt; d. h. dass gilt:
- (1a):
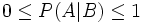
- (2a):
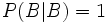
- (3a): Wenn A1 bis Ak paarweise disjunkt sind, so ist
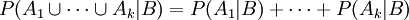
- Beweis: Zu (1a).
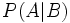 ist Quotient zweier Wahrscheinlichkeiten, für welche nach Axiom (1) gilt
ist Quotient zweier Wahrscheinlichkeiten, für welche nach Axiom (1) gilt 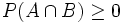 und
und 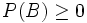 . Da B nicht das unmögliche Ereignis sein soll, ist sogar P(B) > 0. Also gilt auch für den Quotienten
. Da B nicht das unmögliche Ereignis sein soll, ist sogar P(B) > 0. Also gilt auch für den Quotienten 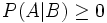 . Ferner sind
. Ferner sind 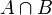 und B\A disjunkt, und ihre Vereinigung ist B. Also ist nach Axiom (3):
und B\A disjunkt, und ihre Vereinigung ist B. Also ist nach Axiom (3):  .
.
Da
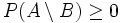 ist, folgt
ist, folgt 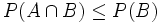 und daher
und daher 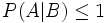 .
.- Zu (2a): Es ist

- Zu (3a): Es ist
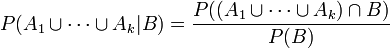
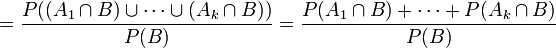
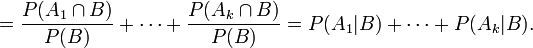
- Dies war zu zeigen.
Beispiel: Es sei wie oben A das Ereignis „Ziehen einer Herz-Karte“ und B das Ereignis „Es ist eine rote Karte“. Dann ist
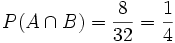 und
und 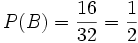 . Folglich
. Folglich  .
.Aus der Definition der bedingten Wahrscheinlichkeit ergeben sich folgende Konsequenzen:
Verbundwahrscheinlichkeit (Schnittmengen von Ereignissen)
Das gleichzeitige Eintreten zweier Ereignisse A und B entspricht mengentheoretisch dem Eintreten des Verbund-Ereignisses
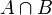 . Die Wahrscheinlichkeit hiervon berechnet sich zur gemeinsamen Wahrscheinlichkeit oder Verbundwahrscheinlichkeit
. Die Wahrscheinlichkeit hiervon berechnet sich zur gemeinsamen Wahrscheinlichkeit oder VerbundwahrscheinlichkeitBeweis. Nach Definition der bedingten Wahrscheinlichkeit ist einerseits
und andererseits auch
Umstellen nach
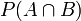 liefert dann sofort die Behauptung.
liefert dann sofort die Behauptung.Beispiel: Es wird eine Karte aus 32 Karten gezogen. A sei das Ereignis: „Es ist ein König“. B sei das Ereignis: „Es ist eine Herz-Karte“. Dann ist
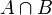 das gleichzeitige Eintreten von A und B, also das Ereignis: „Die gezogene Karte ist ein Herz-König“. Offenbar ist
das gleichzeitige Eintreten von A und B, also das Ereignis: „Die gezogene Karte ist ein Herz-König“. Offenbar ist 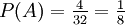 . Ferner ist
. Ferner ist 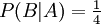 , denn es gibt nur eine Herz-Karte unter den vier Königen. Und in der Tat ist dann
, denn es gibt nur eine Herz-Karte unter den vier Königen. Und in der Tat ist dann  die Wahrscheinlichkeit für den Herz-König.
die Wahrscheinlichkeit für den Herz-König.Bayes-Theorem
Die bedingte Wahrscheinlichkeit von A, vorausgesetzt B, lässt sich durch die bedingte Wahrscheinlichkeit von B, vorausgesetzt A, wie folgt ausdrücken, wenn man die totalen Wahrscheinlichkeiten P(B) und P(A) kennt (Bayes-Theorem).:
Abhängigkeit und Unabhängigkeit von Ereignissen
Ereignisse nennt man unabhängig voneinander, wenn das Eintreten des einen die Wahrscheinlichkeit des anderen nicht beeinflusst. Im umgekehrten Fall nennt man sie abhängig. Man definiert:
- Zwei Ereignisse A und B sind unabhängig, wenn gilt
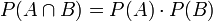 .
.
- Ungenau, aber einprägsam formuliert: Bei unabhängigen Ereignissen kann man die Wahrscheinlichkeiten multiplizieren.
Dass dies dem Begriff „Unabhängigkeit“ gerecht wird, erkennt man durch Umstellen nach P(A):
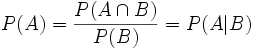 . Das bedeutet: Die totale Wahrscheinlichkeit für A ist ebenso groß wie die Wahrscheinlichkeit für A, vorausgesetzt B; das Eintreten von B beeinflusst also die Wahrscheinlichkeit von A nicht.
. Das bedeutet: Die totale Wahrscheinlichkeit für A ist ebenso groß wie die Wahrscheinlichkeit für A, vorausgesetzt B; das Eintreten von B beeinflusst also die Wahrscheinlichkeit von A nicht.Beispiel: Es wird eine aus 32 Karten gezogen. A sei das Ereignis „Es ist eine Herz-Karte“. B sei das Ereignis „Es ist eine Bild-Karte“. Diese Ereignisse sind unabhängig, denn das Wissen, dass man eine Herz-Karte zieht, beeinflusst nicht die Wahrscheinlichkeit, dass es eine Bild-Karte ist (Der Anteil der Bilder unter den Herz-Karten ist ebenso groß wie der Anteil der Bilder an allen Karten). Offenbar ist P(A) = 8/32 = 1/4 und P(B) = 12/32 = 3/8.
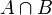 ist das Ereignis „Es ist eine Herz-Bildkarte“. Da es davon drei gibt, ist
ist das Ereignis „Es ist eine Herz-Bildkarte“. Da es davon drei gibt, ist 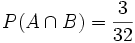 . Und in der Tat stellt man fest, dass
. Und in der Tat stellt man fest, dass 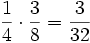 ist.
ist.Ein weiteres lesenswertes Beispiel für sehr kleine und sehr große Wahrscheinlichkeiten findet sich hier: Infinite Monkey Theorem.
Wahrscheinlichkeitstheorie und Statistik
Wahrscheinlichkeitstheorie und mathematische Statistik werden zusammenfassend auch als Stochastik bezeichnet. Beide Gebiete stehen in enger wechselseitiger Beziehung:
- Statistische Verteilungen werden regelmäßig unter der Annahme modelliert, dass sie das Resultat zufälliger Prozesse sind.
- Umgekehrt liefern statistische Daten über eingetretene Ereignisse Anhaltspunkte (in frequentistischer Interpretation sogar die einzigen akzeptablen Anhaltspunkte) für die Wahrscheinlichkeit künftiger Ereignisse.
Anwendungsgebiete
Die Wahrscheinlichkeitstheorie entstand aus dem Problem der gerechten Verteilung des Einsatzes bei abgebrochenen Glücksspielen. Auch andere frühe Anwendungen stammen aus dem Bereich des Glücksspiels.
Heute ist die Wahrscheinlichkeitstheorie eine Grundlage der mathematischen Statistik. Die angewandte Statistik nutzt Ergebnisse der Wahrscheinlichkeitstheorie, um Umfrageergebnisse zu analysieren oder Wirtschaftsprognosen zu erstellen.
Große Bereiche der Physik wie die Thermodynamik und die Quantenmechanik nutzen die Wahrscheinlichkeitstheorie zur theoretischen Erklärung ihrer Resultate.
Sie ist ferner die Grundlage für mathematische Disziplinen wie die Zuverlässigkeitstheorie, die Erneuerungstheorie und die Warteschlangentheorie und das Werkzeug zur Analyse in diesen Bereichen.
Auch in der Mustererkennung ist die Wahrscheinlichkeitstheorie von zentraler Bedeutung.
Siehe auch
Literatur
- Heinz Bauer: Wahrscheinlichkeitstheorie und Grundzüge der Maßtheorie. 4. Auflage. DeGruyter, Berlin 1991, ISBN 3-11-012191-3.
- Richard M. Dudley: Real Analysis and Probability. Cambridge University Press, Cambridge 2003, ISBN 0-521-00754-2.
- Hans-Otto Georgii: Stochastik. DeGruyter, Berlin 2004, ISBN 3-11-018282-3.
- Ulrich Krengel: Einführung in die Wahrscheinlichkeitstheorie und Statistik. Vieweg, Braunschweig 2005, ISBN 3-528-67259-5.
Wikimedia Foundation.