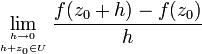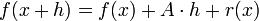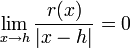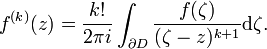- Komplex differenzierbar
-
Holomorphie (von gr. holos, „ganz“ und morphe , „Form“) ist eine Eigenschaft von bestimmten komplexwertigen Funktionen, die in der Funktionentheorie (einem Teilgebiet der Mathematik) behandelt werden. Eine Funktion
 für eine offene Menge
für eine offene Menge 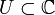 heißt holomorph, falls sie in jedem Punkt aus U komplex differenzierbar ist.
heißt holomorph, falls sie in jedem Punkt aus U komplex differenzierbar ist.Auch wenn die Definition analog zur reellen Differenzierbarkeit ist, zeigt sich in der Funktionentheorie, dass die Holomorphie eine sehr starke Eigenschaft ist. Sie produziert nämlich eine Vielzahl von Phänomenen, die im Reellen kein Pendant besitzen. Beispielsweise ist eine holomorphe Funktion stets unendlich oft differenzierbar und lässt sich lokal in jedem Punkt in eine Potenzreihe entwickeln.
Inhaltsverzeichnis
Definitionen
Es sei
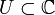 eine offene Teilmenge der komplexen Ebene und
eine offene Teilmenge der komplexen Ebene und 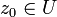 ein Punkt dieser Teilmenge. Eine Funktion
ein Punkt dieser Teilmenge. Eine Funktion  heißt komplex differenzierbar im Punkt z0, falls der Grenzwert
heißt komplex differenzierbar im Punkt z0, falls der Grenzwertexistiert. In diesem Fall bezeichnet man diesen Grenzwert als
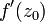 .
.Die Funktion f heißt holomorph im Punkt z0, falls eine Umgebung von z0 existiert, in der f komplex differenzierbar ist. Ist f auf ganz
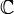 holomorph, so nennt man f eine ganze Funktion.
holomorph, so nennt man f eine ganze Funktion.Erläuterungen
Unterschied zwischen komplexer und reeller Differenzierbarkeit
Zu beachten ist, dass es, im Gegensatz zu reeller Differenzierbarkeit, nicht nur zwei, sondern unendlich viele Möglichkeiten gibt, sich dem Punkt z zu nähern. Komplexe Differenzierbarkeit ist also eine starke Eigenschaft.
Nicht jede reell differenzierbare Funktion
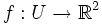 mit
mit  ist also, wenn man sie in naheliegender Weise als Funktion auf
ist also, wenn man sie in naheliegender Weise als Funktion auf 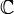 auffasst, auch holomorph. Im Reellen heißt eine Funktion differenzierbar, falls eine
auffasst, auch holomorph. Im Reellen heißt eine Funktion differenzierbar, falls eine 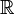 -lineare Abbildung A existiert, so dass die Gleichung
-lineare Abbildung A existiert, so dass die Gleichunggilt, wobei r eine Funktion mit
ist. Für holomorphe Funktionen muss A natürlich
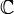 -linear sein, was eine starke Einschränkung bedeutet.
-linear sein, was eine starke Einschränkung bedeutet.Zusammenhang zwischen komplexer und reeller Differenzierbarkeit
Eine Funktion
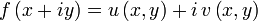 ist genau dann komplex differenzierbar, wenn u,v stetig partiell differenzierbar sind und die cauchy-riemannschen Differentialgleichungen
ist genau dann komplex differenzierbar, wenn u,v stetig partiell differenzierbar sind und die cauchy-riemannschen Differentialgleichungen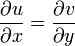 und
und 
erfüllt sind.
Beispiele
Folgende Funktionen sind holomorph auf ganz
 :
:- jedes Polynom
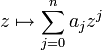 mit Koeffizienten
mit Koeffizienten 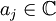
- die Exponentialfunktion exp
- die trigonometrischen Funktionen sin und cos
- die hyperbolischen Funktionen sinh und cosh
Folgende Funktionen sind in keinem komplex differenzierbar und damit auch nirgendwo holomorph:
komplex differenzierbar und damit auch nirgendwo holomorph:- die Betragsfunktion
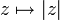
- die Projektionen auf den Realteil
 beziehungsweise auf den Imaginärteil
beziehungsweise auf den Imaginärteil 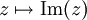
- die komplexe Konjugation
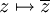
Eigenschaften
Hier folgt eine Auflistung fundamentaler Eigenschaften holomorpher Funktionen, die allesamt kein Pendant in der reellen Theorie besitzen. In der Folge sei
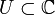 ein Gebiet und
ein Gebiet und 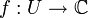 holomorph.
holomorph.Cauchyscher Integralsatz
Ist
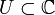 einfach zusammenhängend und γ ein Zyklus in U, so gilt der cauchysche Integralsatz
einfach zusammenhängend und γ ein Zyklus in U, so gilt der cauchysche IntegralsatzCauchysche Integralformel
- Sei D: = Ur(a) die offene Kreisscheibe mit Radius r um den Punkt
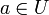 , die ganz in U liegt. Dann gilt für alle
, die ganz in U liegt. Dann gilt für alle 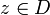 und
und 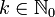 die cauchysche Integralformel
die cauchysche Integralformel
Der Funktionswert eines Punktes in einem Gebiet hängt also nur von den Funktionswerten am Rand dieses Gebietes ab. Für mehrdimensionale holomorphe Abbildungen gibt es ein Analogon. Dieses ist unter dem Namen bochner-martinellische Integralformel bekannt.
Holomorphie und Analytizität
Eine Folgerung aus der cauchyschen Integralformel ist, dass in der komplexen Ebene der Begriff der Analytizität äquivalent zur Holomorphie ist: Jede in z0 holomorphe Funktion ist in z0 analytisch. Umgekehrt lässt sich jede in z0 analytische Funktion zu einer in z0 holomorphen Funktion fortsetzen.
Da Potenzreihen unendlich oft komplex differenzierbar sind (und zwar durch gliedweise Differentiation), erhält man insbesondere, dass holomorphe Funktionen unendlich oft differenzierbar und alle ihre Ableitungen wiederum holomorphe Funktionen sind. Hieran erkennt man schon deutliche Unterschiede zur reellen Differentialrechnung.
Identitätssatz
Es zeigt sich, dass eine holomorphe Funktion schon durch sehr wenig Information eindeutig bestimmt ist. Der Identitätssatz besagt, dass zwei holomorphe Funktionen auf einem Gebiet
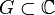 bereits dann auf G identisch sind, wenn sie auf einer geeigneten Teilmenge
bereits dann auf G identisch sind, wenn sie auf einer geeigneten Teilmenge  übereinstimmen. Dabei muss die Übereinstimmungsmenge M noch nicht mal ein kontinuierlicher Weg sein, es reicht aus, dass M einen Häufungspunkt in G besitzt. Diskrete Teilmengen reichen hierfür hingegen nicht aus.
übereinstimmen. Dabei muss die Übereinstimmungsmenge M noch nicht mal ein kontinuierlicher Weg sein, es reicht aus, dass M einen Häufungspunkt in G besitzt. Diskrete Teilmengen reichen hierfür hingegen nicht aus.Weiteres
- Der Satz von Liouville besagt, dass jede beschränkte ganze Funktion konstant ist. Eine einfache Folgerung hieraus ist der Fundamentalsatz der Algebra.
- Ist
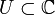 ein Gebiet und
ein Gebiet und 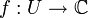 nicht konstant, dann ist
nicht konstant, dann ist 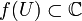 wieder ein Gebiet. (Satz von der Gebietstreue)
wieder ein Gebiet. (Satz von der Gebietstreue)
- Eine Folgerung der Gebietstreue ist das Maximumprinzip.
- Konvergiert eine Folge
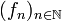 holomorpher Funktionen kompakt auf U gegen die Grenzfunktion f, so ist f wieder holomorph, und man kann Limesbildung und Differentiation vertauschen, das heißt, die Folge (f'n) konvergiert kompakt gegen f'. (Satz von Weierstraß).
holomorpher Funktionen kompakt auf U gegen die Grenzfunktion f, so ist f wieder holomorph, und man kann Limesbildung und Differentiation vertauschen, das heißt, die Folge (f'n) konvergiert kompakt gegen f'. (Satz von Weierstraß).
- Ist die Folge
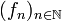 holomorpher Funktionen auf U lokal beschränkt, so existiert eine kompakt konvergente Teilfolge. (Satz von Montel)
holomorpher Funktionen auf U lokal beschränkt, so existiert eine kompakt konvergente Teilfolge. (Satz von Montel)
Biholomorphe Funktionen
Eine Folgerung des Satzes über implizite Funktionen ist, dass für eine holomorphe Funktion, die bijektiv ist, stets auch die Umkehrabbildung holomorph ist. Eine holomorphe und bijektive Abbildung heißt biholomorph.
Holomorphie mehrerer Veränderlicher
Sei
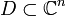 eine komplexe offene Teilmenge. Eine Abbildung
eine komplexe offene Teilmenge. Eine Abbildung  heißt holomorph, falls
heißt holomorph, falls  in jeder Teilfunktion und jeder Variablen holomorph ist.
in jeder Teilfunktion und jeder Variablen holomorph ist.Seien
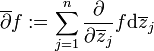 und
und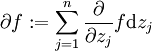
die Dolbeault-Operatoren. Eine äquivalente Definition der Holomorphie einer Funktion f lautet
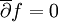 , und für die Ableitungsfunktion gilt
, und für die Ableitungsfunktion gilt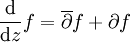 .
.
Hierbei bezeichnen
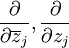 die Wirtingerableitungen, welche definiert sind als
die Wirtingerableitungen, welche definiert sind als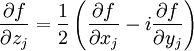 und
und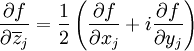 .
.
Die Äquivalenz der Definitionen ist leicht mit Hilfe der cauchy-riemannschen Differentialgleichungen zu erkennen.
Literatur
Standardwerke
Einführungen
- Klaus Jänich: (Die ersten beiden Auflagen unterscheiden sich deutlich von den folgenden. Unter anderem fehlen ab der dritten Auflage die vier „Stern“-Kapitel zu Wirtinger-Kalkül, riemannschen Flächen, riemannschen Flächen eines holomorphen Keimes und algebraischen Funktionen.)
-
- Einführung in die Funktionentheorie. 2. Auflage. Springer-Verlag, Berlin/Heidelberg 1980, ISBN 3-540-10032-6.
-
- Funktionentheorie – Eine Einführung. 6. Auflage. Springer-Verlag, Berlin/Heidelberg 2004, ISBN 3-540-20392-3.
- Wolfgang Fischer, Ingo Lieb: Funktionentheorie – Komplexe Analysis in einer Veränderlichen. 8. Auflage. Vieweg, Braunschweig/Wiesbaden 2003, ISBN 3-528-77247-6.
Ausführliche Darstellungen der Funktionentheorie
- Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 3. Auflage. Springer, 2000, ISBN 3-540-67641-4.
- Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage. Springer, Heidelberg 2002, ISBN 3-540-41855-5.
Siehe auch
Wikimedia Foundation.