- Konstruktions-Remen
-
Vormetrische Längenmaße umfassen alle, insbesondere antike Längenmaße, die vor Festlegung des Meter im Jahr 1799 benutzt wurden. Viele dieser Maße wurden bereits in der Antike von verschiedenen Gelehrten – unter anderem von Herodot, Heron und dem Alexandriner Didymos – beschrieben. Laut diesen Quellen standen viele Maße des Altertums in festen Zahlenverhältnissen, in so genannten Ratios, zueinander.
Einige Forscher aus dem Bereich der historischen Metrologie gehen heute davon aus, dass alle Längenmaße der Antike – zuerst die, des fruchtbaren Halbmondes, sowie des gesamten Mittelmeerraumes, des Nahen und Mittleren Ostens und später auch ganz Europas – jeweils Bezug auf einander nehmen. Wurde ein neues Maßsystem gebildet, so orientierten sich die Metrologen, die es festlegten, stets an schon vorhandenen Maßen der Region.
Forschungen bezüglich antiker Maßsysteme werden seit der Renaissance unternommen. Heute sind die meisten Längenmaße der Antike bekannt, statistisch erfasst und ihre arithmetische Herleitung für viele erklärt. Sehr viele Längenmaße des europäischen Mittelalters scheinen entweder identisch mit den Maßen der Antike zu sein oder können als einfache Ableitungen derselben interpretiert werden. Die Überlieferungslage gibt allerdings keine Anhaltspunkte, wie diese Übereinstimmungen zustande gekommen sein könnten. Historische Traditionen sind zumeist auszuschließen, viele Gleichsetzungen bleiben daher fragwürdig. Die Maße der Antike sind durch archäologische Funde von bisher etwa tausend antiken Maßstäben sowie über Gebäude- und Stadienlängen heute sehr gut ermittelt.
Nach heutigen Erkenntnissen standen insbesondere zwei Ellen am Ursprung der vormetrischen Längenmaße:
- die Nippurelle zu circa 518,5 Millimetern, sowie – letztlich auch von der Nippurelle abgeleitet –
- die ägyptische Königselle zu etwa 529,2 mm. Sie steht im Verhältnis 50 : 49 zur Nippurelle.
Einleitung
Die Metrologie ist eine der ältesten Wissenschaften. Maß und Gewicht sind seit Alters her von außerordentlich großer ökonomischer Bedeutung. Sie gehörten daher immer zu den Regalien. Der schon in der Antike internationale Handel erforderte, dass die Maße in einfachen Ratios vergleichbar waren.
Wurde ein Gebiet erobert oder in ein Abhängigkeitsverhältnis gebracht, konnten die Maße oktroyiert werden. Andererseits konnten sich Metrologen freiwillig in eine Stadt, die durch hervorragende Standards glänzte – im Mittelalter etwa Troyes für Gewichte – begeben, um dort „Maß zu nehmen“.
In beiden Fällen war es nicht ausgeschlossen, dass das übernommene Grundmaß, je nach lokaler Tradition, anders geteilt oder vervielfacht wurde. Selbst innerhalb eines Herrschaftsgebietes war es üblich, verschiedene Maße zu verwenden, die aber stets ihrerseits untereinander feste, bekannte, aus hochzusammengesetzten Zahlen bestehende Verhältnisse einhielten.
So beschreibt zum Beispiel Heron von Alexandria in seiner Geometria[1] eines der griechischen Maßsysteme: „Das Stadion hat 6 Plethren, 60 Maßruten, 400 Ellen, 600 Philetairische Fuß und 720 italische Fuß.“ Die beiden – im folgenden noch häufiger genannten Fußmaße – der Philetairische Fuß, wissenschaftlich pous philetairikos, und der italische Fuß, pous italikos, unterhalten also schon laut Heron die exakte Ratio von 10 : 12, wobei der pous italikos jenem im Agrarmaß Joch, dem iugerum, auf Grund der höheren Teilbarkeit – 28800 gegenbüber 20000 Quadratfuß –, vorgezogen wurde.[2]
Ein weiterer Grund für verschiedene Maße, selbst innerhalb eines Herrschaftsbereiches, war die Besteuerung. Bei Grundbesitz war es durchaus üblich, in Regionen mit Böden, die aus topographischen oder geologischen Gründen einen niederen Ertrag pro Fläche erbrachten, einen Steuernachlass pro Flächeneinheit zu gewähren. Dazu wurden die steuerlich relevanten Feldgrößen modifiziert und die lokalen Messruten angepasst, wobei aber stets darauf geachtet wurde, dass sie in einem einfachen Verhältnis zum Hauptmaß des Landes standen.
So sind seit Alters her sehr viele dieser Ratios bekannt und tradiert. Das antike Stadion zu Athen misst – heute noch nachmessbar – 600 kyrenaische Fuß, was, wie auch in der Antike bekannt, genau 625 römischen Fuß entspricht. Letzterer steht seinerseits zum Beispiel im Verhältnis 30 : 32 zum Pous metrios, einem weiteren wichtigen griechischen Fußmaß.
Die ersten sechs Fußmaße
Aus den beiden Grundmaßen – der mesopotamischen Nippurelle und der ägyptischen Königselle – bildeten sich folgende sechs, direkt abgeleitete Fußmaße:
Teilungsart : Metrologischer Name: Länge in Fingerbreit: Fuß Pous 16 Mazedonische
EllePygme 18 Kretische
EllePygon 20 Klassische
EllePechys 24 Ägyptische
ElleNeilos 28 Mesopotamische
ElleMesopotamos 30 Nubische
ElleNibw * 32 Der „nubische Nippurfuß“ 259,308 291,7215 324,135 388,962 453,789 486,2025 518,616 Der mesopotamische Nippurfuß 276,5952 311,1696 345,744 414,8928 484,0416 518,616 553,1904 Der ägyptische Nippurfuß 296,352 333,396 370,44 444,528 518,616 555,66 592,704 Der ägyptische Nippurfuß wurde später zum römischen Fuß. In Ägypten heißt sein Pygon: Remen. Die Pygme des „nubischen Nippurfußes“ ist der spätere bairische Fuß. Der „nubische Königsfuß“ 264,6 297,675 330,75 396,9 463,05 496,125 529,2 Der „mesopotamische Königsfuß“ 282,24 317,52 352,8 423,36 493,92 529,2 564,48 Der ägyptische Königsfuß 302,4 340,2 378 453,6 529,2 567 604,8 Der „nubische Königsfuß“ wird wissenschaftlich Pous italikos genannt. Sein Mesopotamos ist die babylonische Elle. Seine Pygme ist der hebräische oder latinische Fuß. * Die alte, griechische Nomenklatur der Maße kennt keinen eigenen Namen für die Doppelelle. So wird die 32-Digit-Elle Nibw (sprich: Nibu) genannt, da in Nubien die Elle stets in 32 Fingerbreit geteilt wurde.
Wenn der später römisch genannte Fuß sicher zu recht als ägyptischer Nippurfuß bezeichnet werden kann, so müssen die drei anderen Namen in Anführungsstriche gesetzt werden.
Sie stehen in der obigen Tabelle respektive für: der Fuß der nubisch geteilten Nippurelle, den Fuß der nubisch geteilten Königselle und den Fuß der mesopotamisch geteilten Königselle.Die klassische 24-Daktyloi-Elle wird auch pechys ephtymetrikos genannt. Der Neilos auch pechys neilos sowie der Mesopotamos auch pechys histonikos. Der in der Literatur der Antike auch angeführte pechys thrakikos zu 34 Fingerbreit wird von der heutigen metrologischen Forschung nicht mehr berücksichtigt. In der Tat ist er als Vielfaches innerhalb eines Systems nicht nachzuweisen. Als Ratio zwischen verschiedenen, voneinander abgeleiteten Maßen kann aber die Ratio 17 : 16 tatsächlich auftreten.
Korrekt muss diese Ratio 1701 : 1600 lauten. Die Zahl 1701 ist drei hoch fünf mal sieben. Die Primzahlen 17 und 13 kommen in den alten Systemen nie, die Primzahl 11 fast nie vor. Es verbleiben also zwei, drei, fünf und sieben, das heißt die sieben-glatten Zahlen.
Genau aus diesem Grund optiert man heute sogar für sieben-glatte, konventionelle Absolutwerte. Das Rechnen mit sieben-glatten Werten bedeutet allerdings weder, die antiken Metrologen hätten ihre Längenmaß auf Bruchteile von Mikrometern genau bestimmt, noch, die moderne historische Metrologie könnte heute diesen Wert mit derselben Präzision feststellen. Sieben-glatte Werte stellen nur eine praktische – aber auch klar innerhalb des für die alten Längenmaße ermittelten Variationskoeffizienten liegende – Rundung aller voneinander abgeleiteten Maße dar, um nicht ständig arbiträr dezimal runden zu müssen.
Die in der Tabelle kursiven Werte sind wichtige – seit der Antike bekannte – Längenmaße.
Die davon ab- oder hergeleiteten Maße
Ableitungen direkt von der Nippurelle
Der ursprüngliche mesopotamische Nippurfuß
Die Nippurelle wurde in Mesopotamien – der Ursprungsregion des Sexagesimalsystems – in 30 Fingerbreit geteilt.
- Sechzehn dieser Finger bilden den mesopotamischen Nippurfuß, oder auch einfach nur kurz Nippurfuß genannt.
- Seine Pygme ist in der Literatur als attisch-olympischer Fuß bekannt.
- Sein Pygon wird in der historisch-metrologischen Forschung Indus-Fuß genannt.
- Sein Neilos ist als Salamis-Elle bekannt.
Der ägyptische Nippurfuß oder spätere Römische Fuß
Zu Beginn des dritten Jahrtausends vor Christus übernahmen die alten Ägypter die Nippurelle, teilten diese aber in nur 28 gleiche Teile.
- So entstand der ägyptische Nippurfuß, den die Römer gut 2000 Jahre später als ihren Fuß übernahmen, welhalb er seither römischer Fuß genannt wird.
- Die Pygme dieses Fußes heißt Drusianischer Fuß. Manchmal wird dieser auch als karolingischer Fuß bezeichnet.
- Der Pygon des römischen Fußes heißt im ägyptischen Remen und spielte eine wichtige Rolle in der Findung des ägyptischen Königsfußes.
- Sein Pechys ist natürlich der römische Cubitus.
- Sein Mesopotamos ist die sogenannte Garde-Elle.
- Sein Nibw ist gleich zwei römische Fuß.
Der Fuß der nubisch geteilten Nippurelle
- Teilt man die Nippurelle durch zwei, so erhält man den recht kurzen, selten verwendeten Fuß der nubisch geteilten Nippurelle.
- Die Pygme dieses Fußes jedoch galt in Bayern bis zum 1. Januar 1872 als bairischer Fuß.
- Sein Pygon wurde vielfach von mittelalterlichen Dombauern verwendet (gleich 18 : 16 Baumaß bzw. polnische Fuß.)
- Sein Nibw wurde in der Toskana, bis in die Neuzeit, als florentinisches Maß von den dortigen Landvermessern verwendet.[3]
Ableitungen direkt von der Königselle
Der (neue) ägyptische Königsfuß
Der ägyptische Fuß wurde aufgrund einer trigonometrischen Approximation von den alt-ägyptischen Geometern in 28 Teile geteilt.
- Der ägyptische Königsfuß ist der dazugehörige Fuß dieser Elle. Eventuell ist dieser Fuß – als Shaku – auch bis nach Japan gelangt.
Der Fuß der nubisch geteilten Königselle
- Die halbe ägyptische Königselle ist der Fuß der nubisch geteilten Königselle, der Pous italikos, der von den in Süditalien siedelnden Griechen verwendet wurde.
- Seine Pygme übernahmen die Hebräer von den Babyloniern. Das Maß ist auch als Heraion-Fuß bekannt und wurde in Latium bis in die Neuzeit als latinischer Fuß verwendet.
- In Babylonien wurde dazu ein Mesopotamos zu 30 Digiti gebildet, der als babylonische Elle bezeichnet wird.
Der Fuß der mesopotamisch geteilten Königselle
- Teilt man die ägyptische Königselle direkt durch dreißig, so erhält man den wenig verwendeten Fuß der mesopotamisch geteilten Königselle.
- Seine Pygme ist der bekannte Pous Philetairikos, der seit Heron bekannte Philetarische Fuß. Er gelangte, als „Tschi“ – über die Seidenstraße – vielleicht bis nach China.
- Sein Pygon ist der, ebenfalls weit verbreitete Pous Ptolemaikos, der ptolemäische Fuß.
Mit diesen ersten sechs Ableitungen – die alle schon im dritten Jahrtausend stattgefunden haben – sind bereits etwa die Hälfte aller seit der Antike bekannten Grundmaße erklärt.Weitere Längenmaße der Antike
Der kyrenaische Fuß
Der Nibw des kyrenaischen Fußes steht zur ägyptischen Königselle im Verhältnis 28 : 24. Er entsteht dadurch, dass man den Königsfuß als 24-Finger-Elle behandelt und aus dem neu entstandenen Finger einen Neilos bildet. Die Hälfte dieser neu gebildeten Elle – dann nubisch geteilt – ist der wichtige kyrenaische Fuß.
Der Pechys basilikos
Der Pechys basilikos, wörtlich: „große Elle“, steht zum römischen Doppelfuß im Verhältnis 27 : 30 oder 18 : 20 oder 9 : 10. Sein konventioneller, sieben-glatter Wert lieg bei 533,4336 mm. Sein Fuß, der sogenannte Pous basilikos, hat zu seinem Pechys die Ratio 16 : 24 und ist somit 355,6224 mm lang.
Die samische Elle und ihre Ableitungen
Eine besondere Rolle spielt – nicht zuletzt in der historischen Bauforschung – die samische Elle und die wichtigen, von ihr abgeleiteten Maße.
Die samische Elle steht zur Königselle 80 : 81 und misst somit konventionelle 522 ⅔ mm. Noch in der ersten Hälfte des 20. Jahrhunderts postulierte der Bauforscher Armin von Gerkan einen ionischen Fuß, der zwei Drittel der samischen Elle beträgt, also in etwa 348 4/9 Millimeter. Mit einem „angeblichen ionischen Fuß“ etwa dieser Länge ist aber – nach Angaben des zeitgenössischen Bauforschers de Zwarte – „wenig anzufangen“.[4] Ausgehend von der samischen Elle ergeben sich drei weitere wichtige Fußmaße der Antike:Ratio 20 : 32 Dorischer Fuß = 326 ⅔ mm. Ratio 16 : 28 Ionischer Fuß = 298 ⅔ mm. Ratio 18 : 32 Attischer Fuß = 294 mm. Der dorische Fuß
Der sowohl in der Antike als auch im Mittelalter weit verbreitete dorisch Fuß, seit Herodot (Werke VI, 127) auch pheidonische Fuß genannt, ist der Pygon zur samischen Elle.
Vor dem Maßwechsel in Frankreich unter Colbert 1668 war er auch der offizielle französische Fuß. Das Freiburger Münster wurde offensichtlich ebenfalls nach diesem Fußmaß erbaut. Vereinzelt wird der dorische Fuß auch als „attischer Fuß“ bezeichnet, was aber im Widerspruch zur weitgehend anerkannten Nomenklatur steht.Der ionische Fuß
Als sogenannter ionischer Fuß wird in der modernen historischen Bauforschung nicht mehr der Fuß der samischen Elle als Pechys angesehen (s.o.), sondern jener Fuß, der sich aus der ägyptisch geteilten samischen Elle ergibt, also das Maß zu etwa 298 ⅔ Millimeter. Dieser ionische Fuß tritt auch in den Maßen der Ausgrabungen in Didyma deutlich zu Tage. Die ehemalige österreichische Leinenelle beträgt mit ihren 896 Millimetern ebenfalls drei ionische Fuß.
Der attische Fuß
Sehr viel Verwirrung stiftete in der historischen Metrologie, das im gesamten Mittelmeerraum anzutreffende ca. 294-mm-Maß, also auch 10:9 italische Fuß.
Da dieses Maß auch in Italien weit verbreitet war, wurde der attische Fuß, insbesondere Ende des 19. Jahrhunderts von Paul Guilhiermoz, selbst mit dem römischen Fuß verwechselt. Aufgrund seiner häufigen Präsenz in Italien, konnte sich auch Letronne – ein Mittel bildend zwischen diesem Maß und dem römischen pes monetalis – nur auf etwa 295 mm für den römischen Fuß festlegen. Andere historische Metrologen nennen diesen Fuß heute auch „neu-punischen Fuß“, weil er auch in der Gegend Karthagos nach der römischen Besiedlung Nordafrikas nachzuweisen ist. Bei Ausgrabungen, sowohl im griechischen Kleinasien, als auch auf dem griechischen Festland ist der attischer Fuß zu 294 mm sehr häufig anzutreffen.Wichtige europäische Längenmaße im Verhältnis zu den Maßen der Antike
Der englische Fuß
Der englisch genannte Fuß geht direkt aus dem ebengenannten Pechys basilikos hervor. Der Doppelfuß des ersteren steht zum letzteren im Verhältnis 32 : 28.
Im Jahr 1959 wurde der englische Fuß auf 304,8 mm festgelegt. Die verschiedenen Definitionen davor, im Vereinigten Königreich, im Commonwealth sowie in den Vereinigten Staaten waren ein wenig größer oder kleiner. Der Wert des englischen Fußes von 1959 weicht um nur (304,8 × 2) ÷ (533,4336 ÷ 28 × 32) - 1 = - 0,0063 % vom heutigen Vergleichswert ab.Der französische Fuß
Der Nibw des französisch genannten Fußes steht zu zwei englischen Fuß im Verhältnis 32 : 30.
Der französische Fuß wurde 1799 in der Dezimalmeterdefinition – in Millimeter ausgedrückt – auf genau 9.000.000 ÷ 27.706 mm festgelegt. So ist der Wert des französischen Fußes von 1799 etwa 0,086 % geringer als 16 Fünfzehntel des englischen Fußes von 1959. Bezüglich des 7-glatten Vergleichswertes ist der französische Fuß von 1799 um etwa 0,093 % zu kurz.Der österreichische Fuß
Der später österreichisch genannte Fuß hieß im Altertum Pous metrios.
Er entsteht dadurch, dass der gerade genannte Pous basilikos als Pygme gedeutet wird. Aus dem erhaltenen neuen, kürzeren Digit wird dann der normale Sechzehnfingerfuß gebildet. Er steht also im Verhältnis 16 : 18 zum großen ptolemäischen Fuß und misst somit konventionelle 316,1088 mm. Der im Jahr 1871 empirisch festgestellte Wert lag nur 0,009 % darunter.Der bairische Fuß
Der bereits erwähnte bairische Fuß ist die Pygme zum Fuß der nubisch geteilten Nippurelle. Seine Ratio zum römische Fuß beträgt 63 : 64.
Er wurde 1869 unter König Ludwig II. amtlich auf genau 291,859.206 Millimeter festgelegt, war also 0,047 % länger als der heutige sieben-glatte Vergleichswert.
In der Praxis entstand er dadurch, dass die 1¾ römische Ellen betragende Wiener Elle zuerst durch zweiunddreißig geteilt und dann mit zwölf multipliziert wurde.Der rheinische oder preußische Fuß
Der in Europa sehr weit verbreitete rheinische oder karolingische Fuß wurde 1793 auch zum preußischen Fuß.
Der rheinische Fuß steht zum Fuß der mesopotamisch geteilten Königselle im einfachen Verhältnis von 20 zu 18.
Er steht auch 24 : 25 zum ionischen Fuß, welcher wiederum 20 : 18 zum attischen Fuß steht. Der rheinische Fuß beträgt somit 326 ⅔ ÷ 25 × 24 = 313,6 mm;
64 : 63 kyrenaische Fuß. Der 1872 aufgegebene preußische Fuß war also ca. (313,853 ÷ 313,6 - 1 =) 0,081 % länger als der heutige sieben-glatte Vergleichswert.Der böhmische Fuß
In Prag galt legal eigentlich auch der 1760 von Maria Theresia eingeführte Pous metrios, das heißt der österreichische Fuß.
In der Praxis hielt Böhmen am traditionellen Pous romanikos, also dem römischen Fußes fest, den sie mit 296,380 mm ansetzten[5], etwa 0,009 % mehr als der Vergleichswert.Der latinische Fuß
In Latium wurde von den Landvermessern bis 1863 der in Antike so genannte Pous Heraion verwendet. Dieser ist identisch mit dem hebräischen Fuß.
Es ist die Pygme zum Pous italikos, also der nubisch geteilten Nippurelle und steht auch 18:30 zur babylonischen Elle mit konventionellen 496,125 mm. Der Fuß misst somit 297,675 mm.
Da der Pous italikos auch der ureigene Fuß der in Antike in Süditalien siedelnden Griechen war – daher sein Name – war der Gebrauch seiner Pygme auch in Italien weit verbreitet.Viele historische Metrologen der Frühen Neuzeit und bis ins 19. Jahrhundert verwechselten ihn sogar mit dem römischen Fuß.
Dieser Fuß wurde in Latium mit dem Wert von 297,896 mm verwendet[6], ca. 0,074 % mehr als der sieben-glatte Vergleichswert.Die irrationale, alte Königselle und das Konstruktionsremen
Die Königselle galt in Ägypten – als nie modifiziertes Referenzmaß – über die gesamte ägyptische Geschichte der Antike, außer in den allerersten Jahrhunderten.
In der Tat, für die Zeit vor der 4. Dynastie – also auch noch vor der Zeit der großen Pyramidenbauten – findet die moderne historische Metrologie keinerlei Nachweis für die Verwendung der bekannten ägyptischen Königselle. Es zeigt sich deutlich, dass bis etwa 2700 v.Chr. offensichtlich ein etwa um ein ganzes Prozent kürzeres Maß verwendet wurde.
Dieses alte Maß, das allgemein die alte ägyptische Königselle genannt wird, setzen moderne historische Metrologen mit arbiträren 20 × 30 × 5-2 × 71 × 1871 = 523,88 mm oder – theoretisch um gut 2,4 ppm genauer – gleich 518,616 × (20√2 / 28) Millimeter – an.
Was für die seit Beginn der Menschheitsgeschichte auf allerbeste Präzision erpichten theoretischen Metrologen als inakzeptable Korruption, ja nahezu als Sakrileg erscheinen musste, nämlich eine Differenz von einem vollen Prozent in der Präzision der Längenmaße, das akzeptierten die praktisch orientierten Geometer des Nildeltas mit Freude. Sie hatten – mittels einer trigonometrischen Approximation – einen arbeitstauglichen „Trick“ gefunden, wie sie – nach den jährlichen Nilschwemmen – die irrationale Zahl Wurzel 2 bei der Neuvermessung der Felder praktisch beherrschen konnten.
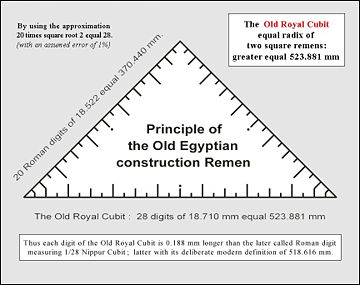
Dazu schufen dazu sie 'ein großes „Geodreieck“, das sogenannte ägyptische Konstruktions-Remen.
Bei diesem betrugen die beiden Katheten jeweils 20 römische Digiti: 20 × 18,522 = 370,44 mm.
Ein Fingerbreit, der durch 28 geteilten Hypotenuse, ist nach dem Satz des Pythagoras: 18,71004543 mm.
Dieser irrationale Wert wird aus praktischen Gründen oft auf 18,71 mm gerundet.Zwar hatten die Geometer ein sich in der Praxis bewährendes Arbeitshilfsmittel geschaffen, die Metrologen aber konnten sich weder mit dem ein Prozent Unterschied abfinden, noch konnten sie eine einfache Ratio zu den von den Nachbarn verwendeten Maßen finden. Sehr bald, schon um 2700 v. Chr., erkannten sie aber, dass, wenn sie als Digitmaß der Katheten statt den, später so genannten römischen Fingerbreit von 18,522 mm, die der (alten) Elle zu 18,71 mm einzusetzen, sie auf der Hypotenuse eine etwas längere Elle erhielten, deren Digits 18,9 mm maßen.
Diese neue Königselle hatte den Vorteil, dass sieben Ellen jetzt genau 12½ später sogenannte römische Fuß ergaben, die neue Königselle mit der Nippurelle also die einfache und genaue Ratio von 50 : 49 unterhielt, da (28 / 20√2) × (28 / 20√2) die rationale Zahl 0,98 ergibt.
Da die Metrologen schon damals einfache Verhältniszahlen zu anderen Maßen schätzten, konnte sich die neue, reformierte Königselle schnell durchsetzen.
Die alte Königselle war folglich von den Ägyptern bereits sehr früh wieder aufgegeben worden, jedoch lebte ihr Digitmaß in der Fingerbreite der Katheten des von Bauingenieuren verwendeten Hilfsmittels, in seiner neuen Version, weiter fort.
Die Bauingenieure des Olympiastadions in Olympia hatten offensichtlich auch ein solches Konstruktionsremen verwendet, dieses aber mit einem griechischen Daktylos-Wert belegt.
Die Katheten ihres Remens maßen (317,52 / 16 × 20 =) 396,9 mm. Es ist also der Pygon, oder auf ägyptisch das Remen, des seit Heron wohlbekannten Philetarische Fußes, der auch Milesischer Fuß genannt wird und selbst wiederum die Pygme des Fußes der mesopotamisch geteilten neuen Königselle darstellt. Die Hypotenuse dieses antiken Baudreiecks der Konstrukteure des antiken Stadion zu Olympia betrug also circa 561,301363 mm. Ein Hypotenusen-Daktylos von etwa 20 325/7000 Millimeter. Im Ergebnis waren somit alle Maße des griechischen Konstruktionsremen im Vergleich zum ägyptischen um die Ratio 30 : 28 erhöht.Der Fuß des Stadions zu Olympia beträgt 16 : 28 der Länge der Hypotenuse des griechischen Konstruktionsremen, also etwa (16 × 20 325/7000 =) 320 5200/7000 Millimeter.
Die Stadionslänge müsste also – ausgehend vom modernen, sieben-glatten, konventionellen Referenzwert – etwa
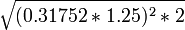
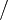
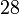
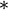
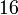
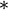
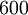

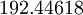 m betragen.
m betragen.Tatsächlich beträgt es – wie es Dieter Lelgemann im Jahr 2004 von seinen Studenten nachmessen ließ[7] – nur 192,27 m, ist also, bezogen auf moderne konventionelle Referenzwertes, etwa 17,6 cm zu kurz. Diese Abweichung liegt aber mit -0,092 % noch sehr gut im Rahmen der Präzision der antiken Maße.
Die Ratios der beiden Remen zum später römisch genannten Fuß
Maße Remen Neues
Remen„Römischer“
FußKonventioneller Wert
in MillimeterRemen 1 : 1 20√2 : 28 20 : 16 20 × 18,522 = 370,440 Neues Remen 28 : 20√2 1 : 1 25√2 : 28 20 × 18,71 = 374,20 „Römischer“ Fuß 16 : 20 28 : 25√2 1 : 1 16 × 18,522 = 296,352 Vor der Reform der Königselle standen das Remen, also die Katheten des alten Konstruktionsremen, und der später römisch genannte Fuß in einem rationalen Verhältnis zueinander.
Die Ratios der beiden Königsellen untereinander und zur Nippurelle
Maße Nippurelle Alte
KönigselleKönigselle Konventioneller Wert
in MillimeterNippurelle 1 : 1 20√2 : 28 49 : 50 28 × 18,522 = 518,616 Alte Königselle 28 : 20√2 1 : 1 20√2 : 28 28 × 18,71 = 523,88 Königselle 50 : 49 28 : 20√2 1 : 1 28 × 18,9 = 529,2 „Römischer“ Fuß 16 : 28 20 : 25√2 28 : 50 16 × 18,522 = 296,352 Seit der Reform der Königselle steht sie zur Nippurelle und zu den „römischen“ Maßen in einem rationalen Verhältnis. Dies bevorzugten die Ägypter seit etwa 2700 v. Chr.
Die Diversifikation der Längenmaße im Mittelalter
Die Diversifikation der verschiedenen Längenmaßsysteme, vor allem im europäischen Mittelalter, bringt es mit sich, dass gerade aus dieser Zeit noch nicht alle Systeme lückenlos aufgeklärt sind. Die Hohheit über Maß- und Gewicht war zunehmend auf kleinere politische Verwaltungseinheiten übergegangen. Ein gemeinsames Maßsystem gab es z.B. im Heiligen Römischen Reich nicht oder nur teilweise, cf. Mark (Gewicht). Kleinere Fürstentümer, Städte mit Marktrecht hatten daneben oft ihre eigenen, regionalen Maßsysteme. Auch Handwerker-Vereinigungen setzten ihre lokalen Maße fest. Als Beispiele hierzu können hier die verschiedenen Schneiderellen und die von den Dombaumeistern verwendeten Maße angeführt werden.
In nicht wenigen Regionen wurden einfach die alten, aus der Antike stammenden Maße bewahrt und weiterverwendet. In anderen Gebieten kamen neue Maße auf, deren Herleitungen heute noch nicht aufgeklärt sind. In manchen Fällen sind trigonometrische Ableitungen nachgewiesen. In anderen Fällen werden Ungenauigkeiten bei der Übertragung bzw. der Bewahrung der Maße vermutet, nämlich immer dann, wenn eine Fehlervermutung das Maß in eine einfache Ratio zu einem bekannten Längenmaßen bringt, sonst aber entweder gar keine, oder nur eine äußerst komplizierte, daher höchst unwahrscheinliche Ableitung gefunden werden kann. Für die wichtigsten Längenmaße, auch des Mittelalters, ist dies aber praktisch ausnahmslos nicht der Fall.
Bekannt sind in der historischen Metrologie auch Fälle von Fehlinterpretation bzw. willentlicher Anpassung an ein Hauptsystem, wenn z.B. ein offensichtlich ganz anders hergeleitetes Tuchmaß, unter in Kaufnahme einer erheblichen Alteration des ursprünglichen Maßes, in ein einfacheres Verhältnis zum Hauptlängenmaß des Landes gebracht wurde.
Belegt sind fernerhin, insbesondere aus dem 19. Jahrhundert, Gesetze über Anpassungen der alten Maße an, entweder die geographische Meile[8] oder auch zum dezimalen Meter selbst, mit jeweils mehr oder weniger großen Abweichungen zu den alten Maßen.
Zwei wichtige, bekannte metrologische Kommata
Aus diesen beschriebenen, gegenseitigen Ableitungen ergeben sich notwendigerweise metrologische Kommata. Diese metrologischen Kommata sind durchaus vergleichbar mit den musikalischen Kommata. Hier wie da, handelt es sich um geringfügige Unterschiede in den absoluten Werten, obwohl es sich um das gleiche Maß bzw. die gleiche Note handelt.
In den Längenmaßen gelten die Ratios 81 : 80, 126 : 125 und 225 : 224 nicht als Kommata, da zum Beispiel die letztere Ratio einen Unterschied von ca. 0,45% bedeutet, was natürlich als ein anderes Längenmaß anzusehen ist.
Die als metrologische Kommata zu betrachtenden Unterschiede verbleiben, im Gegensatz dazu, innerhalb der für die alten Längenmaße ermittelten, statistischen Variationskoeffizienten, das heißt, bezüglich eines hinlänglich belegten und in ausreichender Anzahl statistisch erfassten Normalfußes von knapp 300 mm sind das ca. ± 0,5 Millimeter oder etwa 0,17 Prozent.
Alle kleineren Abweichungen der antiken und mittelalterlichen Längenmaße können als Kommata gelten.
- 2401 : 2400 = 20 × 30 × 50 × 74 : 25 × 31 × 52 × 70 = 1,000 416. Es handelt sich hierbei um das so genannte (common) comma, also das (gemeine) Komma.
- 4375 : 4374 = 20 × 30 × 54 × 71 : 21 × 37 × 50 × 70 ≤ 1,000 229. Es handelt sich hierbei um das so genannte poppy-seed comma, also das Mohnkorn-Komma.
Natürlich war den Metrologen der Antike zum Beispiel der Unterschied zwischen 492 : (402 × 3÷2) = 2401 : 2400 durchaus bekannt. Dennoch spielte dieser Unterschied, sowohl im Altertum und als im auch Mittelalter, in der Praxis, einerseits wegen seiner Geringfügigkeit und andererseits aufgrund der mangelnden präzisen Absolutwerte der alten Maße, keine Rolle.
Eine Multiplikation dieser beiden Kommata, ist das dezimalmetrische Komma von 250 047 zu 250 000, gleich genau 1,000 188. (Vergleiche hierzu das Lemma: kyrenaischer Fuß.)Des Weiteren kann man von metrologischen Kommata sprechen, die aufgrund der sehr verschiedenen, nationalen Definitionen der alten Maße im 19. und 20. Jahrhundert entstanden.
So ist zum Beispiel die Ratio (53 × 127 =) 15875 : 15876 (= 22 × 34 × 72) das Komma des angelsächsischen Kompromissfußes von 1959 zu dezimal-metrisch gerundeten 304,8 mm.Literatur
- Friedrich Hultsch: Griechische und römische Metrologie. 2. Auflage. Berlin 1882.
- Eberhard Knobloch, Dieter Lelgemann, Andreas Fuls: Zur hellenistischen Methode der Bestimmung des Erdumfangs und zur Asienkarte des Klaudios Ptolemaios. In: Zeitschrift für Geodäsie, Geoinformation und Landmanagment 128 (3/2003). S. 211-217.
Weblinks
- Vormetrische Längeneinheiten Von Rolf C. A. Rottländer, Rottenburg / Köln
- „On the Ancient Determination of Meridian Arc Length by Eratosthenes of Kyrene“ - Dieter Lelgemann, Workshop History of Surveying and Measurement, Athens, Greece, May 22-27, 2004 (PDF)
- „Recovery of the Ancient System Foot/Cubit/Stadion“ - Dieter Lelgemann, Workshop History of Surveying and Measurement, Athens, Greece, May 22-27, 2004 (PDF)
Einzelnachweise
- ↑ Heron von Alexandria, Geometria, Heiberg, 1912, ISBN 3-519-01416-5, Seite 403, Absatz 12. Siehe auch das Tabellenfragement des Heron, Fragmente 2, 2 und ein dem Didymos Chalkenteros von Alexandria untergeschobenes Werk Περὶ μαρμάρων καὶ παντοίων ξύλων (Über alle Marmor- und Holzarten) 16.
- ↑ Heron von Alexandria, Geometria, Heiberg, 1912, ISBN 3-519-01416-5, Seite 413, Absatz 67 ff.
- ↑ MARTINI, Angelo, Manuale di metrologia ossia misure, pesi e monete, Torino, Loescher, 1883. Seite 206: Florenz.
- ↑ R. de Zwarte: Der ionische Fuß und das Verhältnis der römischen, ionischen und attischen Fußmaße zueinander. In: Bulletin Antieke Beschaving. Bd. 69, 1994, Seite 131.
- ↑ MARTINI, Angelo, Manuale di metrologia ossia misure, pesi e monete, Torino, Loescher, 1883. Seite 577: Prag.
- ↑ MARTINI, Angelo, Manuale di metrologia ossia misure, pesi e monete, Torino, Loescher, 1883. Seite 596: Rom.
- ↑ Recovery of the Ancient System of Foot/Cubit/Stadion – Length Units, 2004 by Dieter Lelgemann, Germany
- ↑ MARTINI, Angelo, Manuale di metrologia ossia misure, pesi e monete, Torino, Loescher, 1883. Seite 783: Turin.
Wikimedia Foundation.