Calabi-Yau-Mannigfaltigkeit — Ein Schnitt durch eine Calabi Yau, die Quintik Mit Calabi Yau Mannigfaltigkeit, kurz Calabi Yau, bezeichnet man in der Mathematik spezielle komplexe Mannigfaltigkeiten, die eine Rolle in der algebraischen Geometrie spielen. Die theoretische… … Deutsch Wikipedia
Kählermannigfaltigkeit — In der Mathematik bezeichnet man mit Kählermannigfaltigkeit (nach Erich Kähler) eine glatte Mannigfaltigkeit zusammen mit einer komplexen Struktur und einer riemannschen Metrik (im Sinne einer riemannschen Mannigfaltigkeit), die miteinander… … Deutsch Wikipedia
Calabi-Yau — Ein Schnitt durch eine Calabi Yau, die Quintik Mit Calabi Yau Mannigfaltigkeit, kurz Calabi Yau, bezeichnet man in der Mathematik spezielle komplexe Mannigfaltigkeiten, die eine Rolle in der algebraischen Geometrie spielen. Die theoretische… … Deutsch Wikipedia
Calabi-Yau-Raum — Ein Schnitt durch eine Calabi Yau, die Quintik Mit Calabi Yau Mannigfaltigkeit, kurz Calabi Yau, bezeichnet man in der Mathematik spezielle komplexe Mannigfaltigkeiten, die eine Rolle in der algebraischen Geometrie spielen. Die theoretische… … Deutsch Wikipedia
Monge-Ampere-Gleichung — Eine monge ampèresche Gleichung, oder monge ampèresche Differentialgleichung, ist eine spezielle nichtlineare partielle Differentialgleichung zweiter Ordnung in n Variablen. Sie wurde von Gaspard Monge Anfang des 19. Jahrhunderts eingeführt, um… … Deutsch Wikipedia
Monge-Ampere Gleichung — Eine monge ampèresche Gleichung, oder monge ampèresche Differentialgleichung, ist eine spezielle nichtlineare partielle Differentialgleichung zweiter Ordnung in n Variablen. Sie wurde von Gaspard Monge Anfang des 19. Jahrhunderts eingeführt, um… … Deutsch Wikipedia
Monge-Amperesche Gleichung — Eine monge ampèresche Gleichung, oder monge ampèresche Differentialgleichung, ist eine spezielle nichtlineare partielle Differentialgleichung zweiter Ordnung in n Variablen. Sie wurde von Gaspard Monge Anfang des 19. Jahrhunderts eingeführt, um… … Deutsch Wikipedia
Claire Voisin — am IHÉS, 2007 Claire Voisin (* 4. März 1962 in Saint Leu la Forêt) ist eine französische Mathematikerin, die sich mit algebraischer Geometrie beschäftigt. Inhaltsverzeichnis … Deutsch Wikipedia
Charakteristisches Dreieck — Historisch war der Begriff des Differentials bzw. Differenzials im 17. und 18. Jahrhundert der Kern der Entwicklung der Differentialrechnung. Ab dem 19. Jahrhundert wurde die Analysis durch Augustin Louis Cauchy und Karl Weierstrass auf der… … Deutsch Wikipedia
Differenzial (Mathematik) — Historisch war der Begriff des Differentials bzw. Differenzials im 17. und 18. Jahrhundert der Kern der Entwicklung der Differentialrechnung. Ab dem 19. Jahrhundert wurde die Analysis durch Augustin Louis Cauchy und Karl Weierstrass auf der… … Deutsch Wikipedia
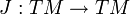 eine komplexe Struktur und
eine komplexe Struktur und 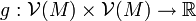 , wobei
, wobei 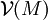 der Raum der Vektorfelder auf
der Raum der Vektorfelder auf 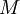 ist, eine Riemannsche Metrik. Das Tripel
ist, eine Riemannsche Metrik. Das Tripel 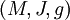 heißt Kählermannigfaltigkeit, wenn
heißt Kählermannigfaltigkeit, wenn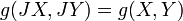 und
und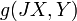 definiert eine symplektische Form
definiert eine symplektische Form 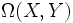 ,
,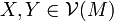 gilt.
gilt.