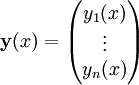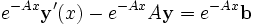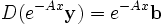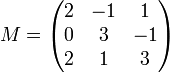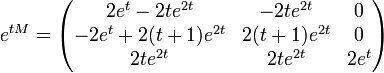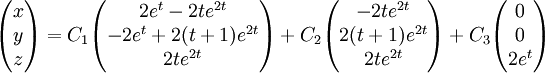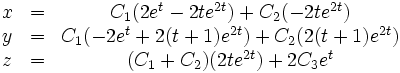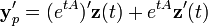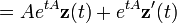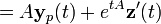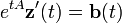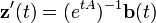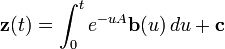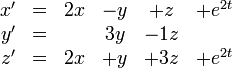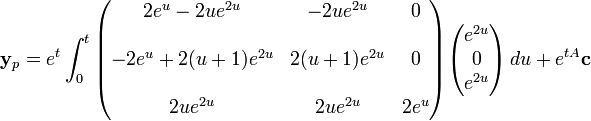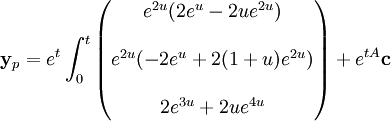- Matrixexponenzial
-
In der Mathematik ist das Matrixexponential oder Matrixexponenzial eine Funktion auf der Menge der quadratischen Matrizen, welche analog zur reellen Exponentialfunktion definiert ist. Das Matrixexpontial stellt die Verbindung zwischen Liealgebra und der zugehörigen Liegruppe her.
Sei X eine reelle oder komplexe n×n-Matrix. Das Exponential von X, welches durch eX oder exp(X) bezeichnet wird, ist die n×n-Matrix, welche durch die folgende Potenzreihe definiert ist.
Diese Reihe konvergiert immer. Daher ist das Exponential von X wohldefiniert. Wenn X eine 1×1-Matrix ist, entspricht das Matrixexponential von X der gewöhnlichen Exponentialfunktion.
Inhaltsverzeichnis
Eigenschaften
Das Matrixexponential teilt eine Reihe der Eigenschaften der gewöhnlichen Exponentialfunktion. Beispielsweise ist das Exponential der n×n-Nullmatrix 0 gleich der n×n-Einheitsmatrix E:
Für beliebige komplexe n×n-Matrizen X und beliebige komplexe Zahlen a und b gilt
Daraus folgt
d.h.
Dabei bezeichnet
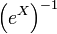 die zu eX inverse Matrix.
die zu eX inverse Matrix.Die Exponentialfunktion erfüllt
 für alle Zahlen x and y. Dasselbe gilt für kommutierende Matrizen X und Y, d.h. aus
für alle Zahlen x and y. Dasselbe gilt für kommutierende Matrizen X und Y, d.h. ausfolgt
Für nichtkommutierende Matrizen braucht diese Gleichung nicht zu gelten. In diesem Fall kann man eX + Y mit Hilfe der Baker-Campbell-Hausdorff-Formel berechnen.
Das Exponential der zu X transponierten Matrix ist gleich der Transposition des Exponentials von X:
Daraus folgt, dass die Matrixexponentialfunktion symmetrische Matrizen auf symmetrische Matrizen und schiefsymmetrische Matrizenen auf orthogonale Matrizen abbildet. Analog gilt zwischen Adjunktion und Transposition die Beziehung
so dass die Matrixexponentialfunktion hermitesche Matrizen auf hermitesche Matrizen und schiefhermitesche Matrizen auf unitäre Matrizen abbildet.
Weiterhin gilt:
- Wenn Y invertierbar ist, dann ist
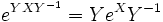 .
. - det(eX) = etr(X). Hier bezeichnet tr(X) die Spur der quadratischen Matrix X.
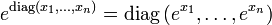 .
.
Die Exponentialabbildung
Das Exponential einer Matrix ist immer eine invertierbare Matrix. Die Inverse von eX ist durch e−X gegeben. Das Matrixexponential liefert somit eine Abbildung
aus dem Vektorraum aller n×n-matrizen in die allgemeine lineare Gruppe, die Gruppe aller invertierbaren Matrizen. Diese Abbildung ist surjektiv, d.h. jede invertierbare Matrix kann als die Exponentialmatrix einer anderen Matrix geschrieben werden. (Dies gilt nur wenn man als Einträge komplexe Zahlen zulässt. Lässt man nur reelle Zahlen zu, so gilt die Aussage nicht.) Der Matrixlogarithmus liefert die Umkehrung dieser Abbildung.
Für je zwei Matrizen X und Y, gilt
wobei || · || eine beliebiege Matrixnorm bezeichnet. Daraus folgt, dass die Exponentialabbildung stetig und auf kompakten Teilmengen von Mn(C) sogar lipschitzstetig ist.
Die Zuordnung
definiert eine glatte Kurve in der allgemeinen linearen Gruppe, welche für t = 0 die Einheitsmatrix liefert. Dies liefert eine Einparameter-Untergruppe der allgemeinen linearen Gruppe, da
gilt. Die Ableitung dieser Funktion am Punkt t ist durch
gegeben. Die Ableitung für t = 0 ist gerade die Matrix X, d. h. X erzeugt diese Einparameter-Untergruppe.
Allgemeiner gilt:
Beispiele von Liealgebren und zugehörigen Liegruppen
Liegruppe Beispiel Allgemeine lineare Gruppe: GL(n,K) Orthogonale Gruppe: O(n,K) Unitäre Gruppe: 
Spezielle unitäre Gruppe: SU(n) 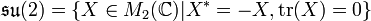 wird von exp surjektiv auf
wird von exp surjektiv auf 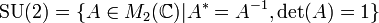 abgebildet.
abgebildet.Spezielle orthogonale Gruppe: SO(n,K)  (schiefsymmetrische Matrizen) wird von exp surjektiv auf
(schiefsymmetrische Matrizen) wird von exp surjektiv auf  abgebildet.
abgebildet.Spezielle lineare Gruppe: SL(n,K) 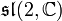 wird von exp nicht surjektiv auf
wird von exp nicht surjektiv auf 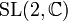 abgebildet. Notorisches Gegenbeispiel
abgebildet. Notorisches Gegenbeispiel  mit
mit 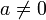 liegt nicht im Bild von
liegt nicht im Bild von 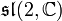 .
.Aus dem letzten Beispiel ist ersichtlich, dass die Exponentialabbildung für die Erzeugung von Liegruppen (je nach Liealgebra) im Allgemeinen nicht surjektiv ist.
Lineare Differentialgleichungen
Einer der Vorzüge des Matrixexponentials ist, dass man es benutzen kann, um Systeme von linearen gewöhnlichen Differentialgleichungen zu lösen. Aus Gleichung (1) unten folgt zum Beispiel, dass die Lösung des Anfangswertproblems
wobei A eine Matrix ist, durch
gegeben ist. Das Matrixexponential kann auch zur Lösung der inhomogenen Gleichung
verwendet werden. Beispiele findet man unten im Kapitel Anwendungen.
Für Differentialgleichungen der Form
mit nicht-konstantem A gibt es keine geschlossenen Lösungen. Die Magnus-Reihe liefert jedoch eine Lösung als unendliche Summe.
Berechnung des Matrixexponentials
Diagonalisierbare Matrizen
Ist die Matrix A eine Diagonalmatrix
dann kann man ihr Exponential ermitteln, indem man die übliche Exponentialfunktion auf jeden Eintrag der Hauptdiagonalen anwendet:
Damit kann man auch das Exponential diagonalisierbarer Matrizen berechnen. Wenn A = UDU−1 mit einer Diagonalmatrix D ist, dann ist eA = UeDU−1.
Nilpotenter Fall
Eine Matrix N ist nilpotent, wenn Nq = 0 für eine geeignete natürliche Zahl q gilt. In diesem Fall kann das Matrixexponential eN direkt aus der Reihenentwicklung berechnet werden, da die Reihe nach einer endlichen Anzahl von Termen abbricht:
Allgemeiner Fall
Eine beliebige Matrix X kann eindeutig in eine Summe
zerlegt werden, wobei
- A diagonalisierbar ist
- N nilpotent ist
- A mit N kommutiert (d.h. AN = NA)
Damit kann man das Exponential von X berechnen, indem man es auf die vorgenannten Fälle reduziert:
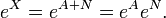 Im letzten Schritt benötigt man die Kommutativität von A und N.
Im letzten Schritt benötigt man die Kommutativität von A und N.Eine andere (nah verwandte) Methode ist die Verwendung der Jordanschen Normalform von X. Sei J die Jordansche Normalform von X mit der Übergangsmatrix P, das heißt, es gilt
Wegen
gilt
Daher muss man nur das Exponential eines Jordan-Blocks kennen. Nun ist jeder Jordan-Block von der Form
wobei N eine spezielle nilpotente Matrix ist. Das Exponential des Jordan-Blocks ist also
Leider ist die Jordan-Normalform-Zerlegung numerisch instabil, da aufgrund der Gleitkommaarithmetik Rundungsfehler in die Eigenwerte eingeführt werden, die eine Gruppierung der Eigenwerte in Gruppen identischer Eigenwerte unmöglich macht.
Numerische Verfahren
Einer der effektivsten verfügbaren Algorithmen ist die Padé-Approximation mit Skalieren und Quadrieren. Bei großen Matrizen kann der Rechenaufwand zusätzlich reduziert werden, indem Krylovräume verwendet werden, deren Basisvektoren mit dem Arnoldi-Verfahren orthogonalisiert worden sind.
Berechnung
Man betrachte die Matrix
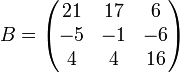 ,
,
welche die Jordansche Normalform
 ,
,
mit der Übergangsmatrix
hat. Dann gilt
und
Somit ist
Das Exponential einer 1×1-Matrix ist trivial. Mit eJ1(4)=e4 folgt
Die Jordansche Normalform und daraus das Exponential zu berechnen, ist auf diesem Weg sehr mühsam. Meist reicht es, die Wirkung der Exponential-Matrix auf einige Vektoren zu berechnen.
Anwendungen
Lineare Differentialgleichungen
Das Matrixexponential kann für die Lösung eines System von Differentialgleichungen verwendet werden. Eine Differentialgleichung der Form
- y′ = Cy
hat die Lösung eCx. Wenn man Vektor
betrachtet, dann kann man ein System von gekoppelten linearen Differentialgleichung betrachten als
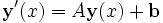 .
.
Wenn man den Integrationsfaktor e−Ax ansetzt und auf beiden Seiten multipliziert, erhält man
Wenn man eAx berechnet, erhält man eine Lösung des Differentialgleichungssystems.
Beispiel (homogen)
Gegeben seien folgende Differentialgleichungen
Die zugehörige Matrix ist
Daraus errechnen wir das zugehörige Matrixexponential
Damit ist die allgemeine Lösung des Differentialgleichungssystems
bzw.
Inhomogener Fall - Variation der Konstanten
Für den inhomogenen Fall kann man eine Methode ähnlich der Variation der Konstanten benutzen. Es wird ein Lösung der Form yp(t)=exp(tA)z(t) gesucht:
Um die Lösung yp zu ermitteln, setzt man
Damit ergibt sich
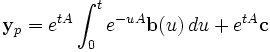
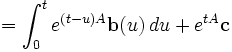 ,
,
wobei c durch die Anfangsbedingungen bestimmt wird.
Beispiel (inhomogen)
Gegeben sei das System von Differentialgleichungen
Damit ergibt sich folgende Matrix
und
Von oben kennen wir die allgemeine Lösung der homogenen Gleichung.
Die Summe aus homogenen und speziellen Lösungen ergeben die Lösung für das inhomogene Problem. Man muss jetzt nur noch die spezielle Lösung finden (über die Variation der Konstanten).
Von der Gleichung oben erhält man:
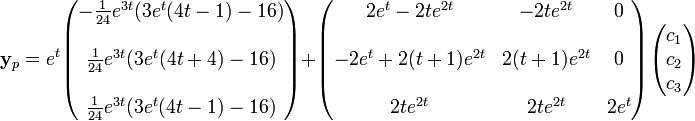 ,
,
welche weiter vereinfacht werden kann, um die notwendige spezielle Lösung durch Variation der Konstanten zu bestimmen.
Siehe auch
Literatur
- Roger A. Horn and Charles R. Johnson. Topics in Matrix Analysis. Cambridge University Press, 1991. ISBN 0-521-46713-6 (englisch).
Weblinks
- Claudia Würz. Gruppen in der Physik - Liegruppen und Liealgebren 1.Teil. Vortrag vom 13.06.2006.
- Ferienserie.pdf (ETH Zürich, 2008).
Wikimedia Foundation.

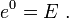
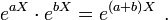
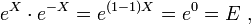
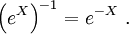
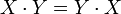
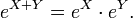
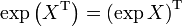
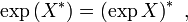

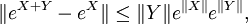
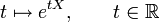
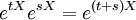
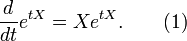

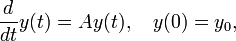

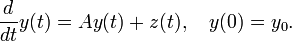
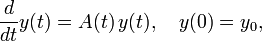

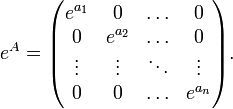
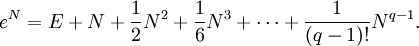
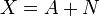
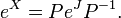
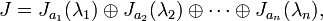
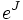
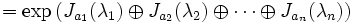
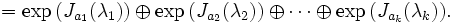
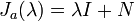
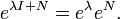
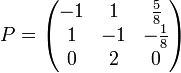
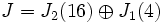
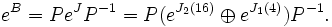
![\exp \left[ 16 E+\begin{pmatrix} 0 & 1 \\
0 & 0 \end{pmatrix} \right] = e^{16}\left[\begin{pmatrix} 1 & 0 \\
0 & 1 \end{pmatrix} + \begin{pmatrix} 0 & 1 \\
0 & 0 \end{pmatrix} + {1 \over 2!}\begin{pmatrix} 0 & 0 \\
0 & 0 \end{pmatrix}+\cdots\right]=\begin{pmatrix} e^{16} & e^{16} \\
0 & e^{16} \end{pmatrix}](/pictures/dewiki/100/d617d19d6c3b3e5c72bfec583c863101.png)