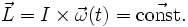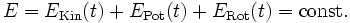- Mechanik starrer Körper
-
Dieser Artikel wurde aufgrund von inhaltlichen Mängeln auf der Qualitätssicherungsseite des Portals Physik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Physik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Hilf mit, die inhaltlichen Mängel dieses Artikels zu beseitigen, und beteilige dich an der Diskussion.
Ein starrer Körper ist ein physikalisches Modell eines nicht verformbaren Körpers. Hierfür erfolgt eine Idealisierung durch die Annahme, dass zwei beliebige Punkte des Körpers unabhängig von äußeren Kräften immer den gleichen Abstand zueinander besitzen. In der klassischen Mechanik wird dabei eine kontinuierliche Massenverteilung und in der Quantenmechanik ein System von diskreten Massenpunkten (z. B. Atome, Moleküle) zugrunde gelegt.
Die Mechanik starrer Körper befasst sich mit der Bewegung starrer Körper unter dem Einfluss äußerer Kräfte. Durch die Modellvoraussetzungen treten dabei ausschließlich Bewegungen des gesamten Körpers in eine Richtung (Translationsbewegungen) und Rotationsbewegungen auf. Zusätzliche Bewegungsformen, wie Schwingungen einzelner Massenpunkte oder Verformungen des Körpers, werden durch die allgemeinere Mechanik fester Körper behandelt.
Ein starrer Körper ohne Translationsbewegung wird als Kreisel bezeichnet.
Inhaltsverzeichnis
Allgemeine Bewegungen starrer Körper
Die Massenpunkte eines starren Körpers haben bezüglich eines körperfesten Bezugssystems (Schwerpunktsystem) (zeitlich) konstante Raumkoordinaten. Aus einer ruhenden Betrachtung (Laborsystem) heraus setzt sich eine freie Bewegung (ohne Einwirkung äußerer Kräfte) als Folgerung des Schwerpunktsatzes aus zwei unabhängigen Bewegungsformen zusammen:
- einer geradlinigen Bewegung des Schwerpunktes
- einer Drehbewegung des Körpers um eine (freie) Rotationsachse
Jede solche Bewegung ist äquivalent zu einer Schraubenbewegung. Dies bedeutet, dass sich zu einer gegebenen Bewegung eines starren Körpers zu jedem Zeitpunkt eine Schraubenlinie angeben lässt, die die ursprüngliche Raumposition und Orientierung in die aktuelle überführt (Theorem von Chasles: Michel Chasles, 1832). Eine Allgemeine Bewegung starrer Körper (mit äußeren Kräften) kann somit durch eine Folge von Schraubenbewegungen (sog. Schrotung) beliebig genau angenähert werden.
Aus gruppentheoretischer Sicht lassen sich die Translations- und die Rotationsabbildung jeweils durch die Translationsgruppe T(3) und die Drehgruppe SO(3) erzeugen. Die Komposition beider Abbildungen führt zu der speziellen euklidischen Gruppe SE(3), welche eine Lie-Gruppe ist. Dies ist wichtig, um zu erkennen, dass die Abbildung differenzierbar ist.
Freiheitsgrade und Konfigurationsraum
 Eulersche Winkel zur Beschreibung der Orientierung eines flugzeugfesten Koordinatensystems
Eulersche Winkel zur Beschreibung der Orientierung eines flugzeugfesten KoordinatensystemsDie Freiheitsgrade eines n-Teilchen-Systems bilden einen sogenannten Konfigurationsraum. Dieser setzt sich bei starren Körpern aus drei Freiheitsgraden bezüglich der Position und drei weiteren bezüglich der Orientierung zusammen. Neben verschiedenen ortsfesten Koordinatensystemen, die eine Beschreibung der Position erlauben, bieten die Eulerschen Winkel eine Möglichkeit zur Beschreibung der Orientierung, die besonders in der Luft- und Raumfahrt eine wichtige Rolle einnimmt.
Zur Anschauung kann ein freier Körper wie ein (kunstflugtaugliches) Flugzeug herangezogen werden, welches drei Freiheitsgrade einer geradlinigen Bewegung besitzt, da es sich frei in drei Raumdimensionen bewegen kann. Hinzu kommen drei weitere Freiheitsgrade der Drehungen um räumliche (unabhängige) Drehachsen.
Offensichtlich vermindert nun jede Einschränkung der Bewegungmöglichkeit die Anzahl der Freiheitsgrade. Wird beispielsweise ein Massenpunkt des starren Körpers räumlich fixiert, so kann man in diesen den Ursprung des Bezugssystems legen. Dadurch reduziert sich die Bewegung auf eine reine Änderung der Orientierung und es bleiben nur mehr drei Freiheitsgrade. Wird ein weiterer Punkt festgehalten, so kann der Körper nur noch um eine raumfeste Drehachse rotieren und hat damit nur noch einen Freiheitsgrad, nämlich den Drehwinkel. Legt man schließlich noch einen dritten Punkt des Körpers fest, so verliert er auch den letzten Freiheitsgrad und ist damit bewegungslos. Jede weitere räumliche Fixierung von Punkten führt nunmehr zu einer sogenannten statischen Überbestimmtheit, die in der Statik eine wichtige Rolle spielt.
Formulierung der Allgemeinen Bewegungsgleichung
Wählen wir nun den Ursprung des raumfesten Koordinatensystems so, dass er zum Zeitpunkt t = 0 mit dem Schwerpunkt des Körpers übereinstimmt, so kann die Position eines beliebigen Teilchens mit der von der der Winkelgeschwindigkeit abhängigen Drehmatrix in folgender allgemeinen Bewegungsgleichung beschrieben werden:
Die Ableitung nach der Zeit ergibt:
dabei bezeichnen:
- rT(t), vT(t) die vektorielle Position und Geschwindigkeit des Teilchens zum Zeitpunkt t, wobei r0 = rT(0)
- rS(t), vS(t) die vektorielle Position und Geschwindigkeit des Schwerpunktes zum Zeitpunkt t
- A(t) die Drehmatrix in Abhängigkeit von der vektoriellen Winkelgeschwindigkeit ω(t) zum Zeitpunkt t
Da die äußeren Kräfte im allgemeinen jedoch nicht als konstant anzusehen sind und wiederum selbst von Position und Geschwindigkeit im Kraftfeld abhängen können (Reibung), stellt die Bestimmung der Bewegungsgleichung oftmals ein schwieriges Problem dar.
Ansätze zur Bestimmung der Bewegungsgleichung
Nach der Modellvoraussetzung gelten konstante Distanzen zwischen den Teilchen. Aus dem Schwerpunktsatz lassen sich nun einige Folgerungen ziehen:
- Für die Wirkung eines Systems äußerer Kräfte auf einen starren Körper sind nur die resultierende Kraft F und das resultierende Drehmoment M entscheidend. Alle Kräftesysteme mit gleichen Resultierenden sind somit in ihrer Wirkung äquivalent.
- Der Trägheitstensor I eines starren Körpers ist bezüglich eines Schwerpunktsystems konstant.
Häufig werden dem Modell zudem weitere Idealisierungen zugrunde gelegt, die es erlauben sogenannte Erhaltungssätze zur Bestimmung der Bewegungsgleichung einzuführen:
Wird ein abgeschlossenes System angenommen, so folgt aus dem Drehimpulserhaltungssatz, dass der vektorielle Gesamtdrehimpuls L des Systems konstant ist, und es gilt:
dabei bezeichnen:
- I den Trägheitstensor des starren Körpers
- ω(t) die vektorielle Winkelgeschwindigkeit zum Zeitpunkt t
Wird ein konservatives Kraftfeld zugrunde gelegt, so folgt aus dem Energieerhaltungssatz, dass die Gesamtenergie E konstant ist, und es gilt:
dabei bezeichnen:
- EKin(t), EPot(t) die kinetische Energie der Translation und die potentielle Energie zum Zeitpunkt t
- ERot(t) die kinetische Energie der Rotation, bzw die Rotationsenergie zum Zeitpunkt t
Drehung eines starren Körpers um eine raumfeste Achse
Wird die Drehachse festgelegt, so bleibt der Drehwinkel als einziger Freiheitsgrad der Rotation. Die Rotation wird durch die Rotationsgeschwindigkeit ω beschrieben. Diese Größe lässt sich als Vektor schreiben und mit Ort
 und Bahngeschwindigkeit
und Bahngeschwindigkeit  eines Punktes verknüpfen
eines Punktes verknüpfenDiese Gleichung gilt genau dann, wenn als Richtung des Vektors
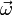 die Rotationsachse gewählt wird. In Richtung des Vektors gesehen findet dabei die Rotation im Uhrzeigersinn statt.
die Rotationsachse gewählt wird. In Richtung des Vektors gesehen findet dabei die Rotation im Uhrzeigersinn statt.Wenn ein Körper um zwei Achsen rotiert, lassen sich für beide Achsen Vektoren zur Winkelgeschwindigkeit definieren. Ihre Summe ergibt dann die Gesamtrotation des Körpers. Es findet also insgesamt nur eine Rotation um eine Achse statt. Damit ist gewährleistet, dass die Winkelgeschwindigkeit als Vektor additiv ist und es daher sinnvoll ist, diese Größe als Vektor darzustellen.
Drehung eines starren Körpers um einen raumfesten Punkt
Eine solche Bewegung heißt auch sphärische Bewegung, weil sich dabei alle Punkte des Körpers auf Kugelschalen („Sphären“) bewegen, deren Mittelpunkt der feste Punkt O ist.
Wir betrachten wieder zwei Punkte A und B des starren Körpers. Durch eine beliebige Bewegung um den festen Punkt O mögen die beiden Punkte in die Endlage A' und B' überführt werden. Wenn wir wieder von dem tatsächlichen Verlauf der Bewegung absehen und nur die Ausgangs- und die Endlage betrachten, so kann der gleiche Effekt stets durch eine Rotation um eine durch den festen Punkt gehende Achse erzielt werden. Es gilt also der Satz: Eine beliebige Bewegung eines starren Körpers um einen festen Punkt ist äquivalent (d. h. hinsichtlich des Ergebnisses gleichwertig) einer Rotation um eine bestimmte, durch diesen Punkt gehende Achse (Eulersches Theorem).
Der Beweis verläuft analog zu dem für die ebene Bewegung.
Die beiden Dreiecke OAA' und OBB' sind gleichschenklig. Wir errichten die mittelsenkrechte Ebene e auf AA' und f auf BB' . Jeder Punkt der Ebene e ist von A und A' gleich weit entfernt, und jeder Punkt der Ebene f ist von B und A'B' gleich weit entfernt. Beide Ebenen gehen durch O und schneiden einander in einer Geraden OC. Alle Punkte dieser Geraden haben die Eigenschaften der Punkte beider Ebenen gemeinsam: sie sind sowohl von A und A' als auch von B und B' gleich weit entfernt. Außerdem ist der Winkel AOC gleich dem Winkel A’OC und der Winkel BOC gleich dem Winkel B'OC.
Jede durch O gehende und in der Ebene e liegende Gerade kann als Drehachse dienen, um A in A' überzuführen. Dasselbe gilt für jede in der Ebene f liegende und durch O gehende Gerade bezüglich der Punkte B und B' . Da die Gerade OC zusammen mit der Strecke AB als starrer Körper aufgefasst werden kann, führt eine Drehung um OC, welche A in A' überführt, auch B in B' über.
Analog zu unserem Vorgehen bei der ebenen Bewegung betrachten wir nun mehrere Zwischenstadien der tatsächlichen Bewegung und nähern jede der Bewegungsphasen durch eine Rotation um eine bestimmte Achse an, die wie oben gefunden werden kann. Die verschiedenen Achsen und die von ihnen bestimmten Ebenen bilden dann einerseits eine im Raum feste Pyramidenfläche (Rastpolpyramide) mit der Spitze in O und andererseits eine im Körper feste (und somit im Raum bewegliche) Pyramidenfläche, die Gangpolpyramide. Beide Pyramiden rollen über die Kanten aneinander ab.
Wenn die Anzahl der betrachteten Bewegungsphasen unbeschränkt zunimmt, gehen die beiden Pyramidenflächen in Kegelflächen über, die aufeinander abrollen und deren Mantellinien die (raumfesten und körperfesten) momentanen Drehachsen sind.
Im Hinblick auf die später zu behandelnde Kreiselbewegung ist insbesondere der Fall interessant, in dem die beiden Kegelflächen kreisförmig sind. Dabei sind zwei Fälle zu unterscheiden: Der Gangpolkegel (blau) kann auf dem Rastpolkegel (rot) außen oder innen abrollen. Dies zeigt die folgenden Abbildung.
Ebene Bewegung eines starren Körpers
Ein Beispiel für die ebene Bewegung eines starren Körpers ist ein Buch, das auf einer Tischplatte bewegt wird. Dabei bewegen sich alle Punkte des Körpers (des Buches) parallel zu einer Ebene (zur Tischplatte). Alle Punkte des Körpers, die auf demselben Lot zur Ebene liegen, bewegen sich dabei auf kongruenten Bahnen. Daher genügt es, den Körper auf eine einzige Ebene – hier eine Seite des Buches – zu reduzieren und lediglich die Bewegung einer Ebene auf einer anderen, festen Ebene zu betrachten.
Diese Bewegung hat drei Freiheitsgrade: Wir können die beiden Koordinaten irgendeines Punktes der beweglichen Ebene beliebig wählen und dann die Ebene noch um diesen Punkt drehen.
Zunächst will ich zeigen, dass man jede beliebige ebene Verschiebung eines Körpers aus einer Position (1) in eine Position (2) als das Ergebnis einer Drehung um einen Punkt auffassen kann. Dabei wird von den Zwischenstadien der Verschiebung völlig abgesehen und es werden nur die Anfangs- und die Endposition betrachtet. Dabei genügt es, zwei in der Bewegungsebene gelegene Punkte A und B des Körpers herauszugreifen, denn durch die Lage dieser beiden Punkte ist auch die Position aller übrigen Punkte des Körpers festgelegt. Durch die betrachtete Verschiebung seien die beiden Punkte A und B auf einem beliebigen Weg in die Position A' bzw. B' bewegt worden. Konstruiert man die Mittelsenkrechten der Strecken AA' und BB' und schneidet sie miteinander, so erhält man das gesuchte Rotationszentrum P. Während der Drehung wird das Dreieck PAB in das kongruente Dreieck PA'B' übergeführt und gleichzeitig werden alle anderen Punkte des Körpers aus ihrer ursprünglichen Lage in eine neue Position gebracht. Da das Drehzentrum für alle Punkte dasselbe ist, würde man denselben Punkt P auch mit zwei beliebigen anderen Punkten (statt A und B) finden.
(Zum vollständigen Beweis muss gezeigt werden, dass dieselbe Drehung, welche die Strecke PA in die Strecke PA' überführt, auch die Strecke PB in die Strecke PB' überführt. Dazu muss bewiesen werden, dass der Winkel APA' gleich dem Winkel BPB' ist. Wegen der Kongruenz der Dreiecke APB und A'PB' sind die Winkel APB und A'PB' gleich. Ich nenne sie α. Nun ist aber Winkel APA' = α + Winkel BPA' und Winkel A'PB' ebenfalls gleich α + Winkel BPA' . Also sind die beiden fraglichen Winkel gleich. – Einfacher ist folgende Argumentation, die später auch noch in einem anderen Zusammenhang benutzt werden kann: Da wir es hier mit einem starren Körper zu tun haben, ist auch das Dreieck ABP ein starres Gebilde. Daher können sich bei einer Rotation um P die beiden Radien PA und PB immer nur um gleiche Winkel drehen.))
Wenn wir nun die Zwischenstadien der Bewegung nicht ignorieren, sondern die Bahnkurven der Punkte A und B exakt verfolgen wollen, so können wir zunächst einige Zwischenstadien der Bewegung betrachten:
Für je zwei benachbarte Lagen der Strecke ’’AB’’ können wir – wie oben – ein temporäres Drehzentrum konstruieren und so die gesamte Ortsveränderung durch eine Anzahl von Drehungen um ein jeweils anderes temporäres Drehzentrum („temporärer Pol“) annähern.
Verbindet man die benachbarten temporären Drehzentren miteinander, so entsteht ein Polygonzug. Es lohnt sich, diesen Vorgang in seinen Phasen in einem Modell zu realisieren. Dazu befestigt man ein Blatt Papier (die feste Ebene) auf einer geeigneten Unterlage (Korkbrett, Weichfaserplatte, Styroportafel …). Ein zweites Blatt Papier (das transparent sein sollte) stellt die bewegte Ebene (den bewegten Körper) dar, auf der zwei Punkte A und B und ihre Verbindungsgerade markiert werden. Anstatt nun aber die einzelnen Phasen der Verschiebung dieser Ebene vorzugeben und dann Mittelsenkrechten über mehreren kleinen Teilstrecken zu errichten und diese paarweise miteinander zu schneiden (was mühsam und ungenau wäre), ist es weitaus bequemer, das Pferd von hinten aufzuzäumen und sich den Polygonzug von temporären Zentren beliebig vorzugeben. Dann wird das transparente Papier auf die feste Ebene gelegt. Mit einer Stecknadel sticht man zunächst in den Punkten A und B durch die beiden Papiere hindurch und markiert so deren Ausgangslage auf der festen Ebene. Dann sticht man im ersten Drehzentrum P1 durch beide Ebenen und dreht das obere Papier um einen beliebigen Winkel (etwa 20° bis 30°), wobei die Stecknadel die Drehachse bildet. Dann sticht man die Nadel durch das zweite Drehzentrum und dreht wiederum die obere Ebene um einen beliebigen Winkel usw. Nach der letzten Drehung markiert man durch Durchstechen die Lage der Punkte Πi auf der festen Ebene und ebenso Endlage der Punkte A und B, die mit A' und B' bezeichnet sind. Dadurch erhält man auf der festen Ebene eine Figur, die etwa so aussieht:
Diese Abbildung lässt sich auch als „Ausschneidebogen“ zur Demonstration verwenden. Dazu schneidet man den linken Teil am blauen Polygonzug entlang aus. Dann legt man die Punkte Π6 und P6 wieder aufeinander und dreht den ausgeschnittenen linken Teil um Π6, bis Π5 auf P5 zu liegen kommt usw. So kann man den ganzen Vorgang rückwärts verfolgen, bis man am Anfang angekommen ist. Von dort kann man den ursprünglichen Ablauf nachvollziehen. Man kann also die wirkliche Bewegung der Ebene (oder des Körpers) annähern, indem man das körperfeste (blaue) Polygon um das raumfeste (rote) Polygon „kantet“.
Wenn wir nun die Anzahl der betrachteten Bewegungspasen unbegrenzt wachsen lassen, so nähert sich der Bewegungsablauf unbeschränkt dem tatsächlichen Vorgang und die beiden Polygone werden zu glatten Kurven, von denen die blaue auf der roten abrollt. So ergibt sich folgender Satz:
Jede beliebige Bewegung eines starren Körpers in einer Ebene kann dadurch erzeugt werden, dass eine bestimmte, im Körper feste Kurve auf einer bestimmten, im Raume festen Kurve abrollt. Die erste Kurve heißt Gangpolkurve oder Körperzentrode, die zweite Rastpolkurve oder Raumzentrode.
Handelt es sich um die ebene Bewegung eines Körpers, so können wir in den Punkten der Rast– und Gangpolkurve Lote auf der festen Ebene errichten. Diese bilden je eine gerade Zylinderfläche, die Gangpolfläche (blau) und die Rastpolfläche (rot), die aufeinander abrollen. [1]
Wikimedia Foundation.