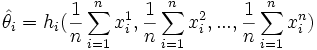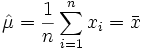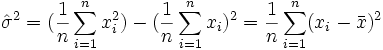Momentenschätzer

Die Momentenmethode ist in der schließenden Statistik ein Schätzverfahren, mit dem man anhand einer Stichprobe die Parameter der theoretischen Verteilung einer Grundgesamtheit schätzen kann. Dazu drückt man diese Parameter in Abhängigkeit von den Momenten (um Null) der Verteilung aus. In einem zweiten Schritt setzt man die empirischen Momente anstatt der Momente in die Gleichungen ein und erhält so die Momentenschätzer. Indem man die Werte einer Stichprobe in den Momentenschätzer einsetzt, erhält man eine Schätzung des entsprechenden Parameters der theoretischen Verteilung.

Die Momentenmethode ist die älteste Schätztechnik und geht auf Karl Pearson zurück. Sie ist in der Anwendung sehr einfach, hat aber den Nachteil, dass die resultierenden Schätzer nicht immer erwartungstreu sind.

Vorgehensweise

1. Die Parameter θ_i der theoretischen Verteilung werden als Funktionen der Momente m_k angegeben:

   θ_i = h_i(m₁,m₂,...,m_n)

2. Die Momentenschätzer 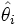$\hat\theta_i$ für die einzelnen Parameter werden berechnet, indem in den obigen Gleichungen die empirischen Momente 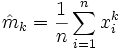$\hat m_k = \frac {1}{n}\sum_{i=1}^n x_i^k$ für die Momente m_k eingesetzt werden:

   $\hat\theta_i = h_i(\frac {1}{n}\sum_{i=1}^n x_i^1, \frac {1}{n}\sum_{i=1}^n x_i^2, ..., \frac {1}{n}\sum_{i=1}^n x_i^n)$

Ein einzelner Parameter kann direkt errechnet werden. Bei mehreren zu schätzenden Parametern ergibt sich häufig ein Gleichungssystem, das bezüglich der unbekannten Parameter aufgelöst werden kann.

Durch Einsetzen der Werte einer Stichprobe erhält man dann Werte für die Parameter der theoretischen Verteilung.

Beispiel

Es wird angenommen, dass die Grundgesamtheit normalverteilt ist. Ausgehend von einer Zufallsstichprobe sollen Erwartungswert μ und Varianz σ² der entsprechenden Zufallsvariable geschätzt werden.

Bei der Normalverteilung gilt E(X) = μ und E(X²) = σ² + μ². Die unbekannten Parameter hängen dann wie folgt von m₁ = E(X) und m₂ = E(X²) ab:

θ₁ = μ = E(X)

θ₂ = σ² = E(X²) − μ² = E(X²) − E(X)²

Setzt man nun die Schätzfunktionen ein, so erhält man die folgenden Schätzungen:

$\hat\mu = \frac {1}{n}\sum_{i=1}^n x_i = \bar x$

$\hat\sigma^2 = (\frac {1}{n}\sum_{i=1}^n x_i^2) - (\frac {1}{n}\sum_{i=1}^n x_i)^2 = \frac {1}{n}\sum_{i=1}^n (x_i - \bar x)^2$

Man sieht, dass σ² nicht erwartungstreu ist, da die Quadratsumme durch n statt n − 1 geteilt wird. Aber sie ist asymptotisch erwartungstreu.

Literatur

• Rainer Schlittgen: Einführung in die Statistik. 9. Auflage. Oldenbourg Wissenschaftsverlag, Oldenbourg 2000, ISBN 3-486-27446-5