- Bild (Kategorientheorie)
-
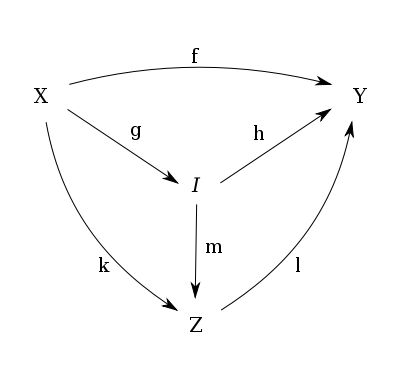
In der Kategorientheorie ist ein Bild eines Morphismus
 ein Unterobjekt
ein Unterobjekt  von Y, das die folgende universelle Eigenschaft hat:
von Y, das die folgende universelle Eigenschaft hat:- Es gibt einen Morphismus
 mit f = hg.
mit f = hg. - Für jedes Unterobjekt
 , das obige Eigenschaft erfüllt (f = lk), gibt es einen eindeutigen Morphismus
, das obige Eigenschaft erfüllt (f = lk), gibt es einen eindeutigen Morphismus  mit k = mg und h = lm.
mit k = mg und h = lm.
Das Kobild eines Morphismus
 ist der duale Begriff: ein Kobild ist ein Quotientenobjekt
ist der duale Begriff: ein Kobild ist ein Quotientenobjekt  von X, das die folgende universelle Eigenschaft hat:
von X, das die folgende universelle Eigenschaft hat:- Es gibt einen Morphismus
 mi f = hg.
mi f = hg. - Für jedes Quotientenobjekt
 , das obige Eigenschaft erfüllt (f = lk), gibt es einen eindeutigen Morphismus
, das obige Eigenschaft erfüllt (f = lk), gibt es einen eindeutigen Morphismus  mit k = mg und h = lm.
mit k = mg und h = lm.
In Kategorien mit Kern und Kokern ist jeder Kern eines Kokerns von f ein Bild von f, jeder Kokern des Kernes ein Kobild.In abelschen Kategorien wie den Kategorien der Vektorräume oder abelschen Gruppen stimmen Bild und Kobild überein. In den genannten Kategorien sind sie auch gleich dem mengentheoretischen Bild.
- Es gibt einen Morphismus
Wikimedia Foundation.