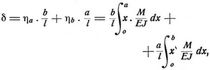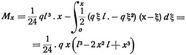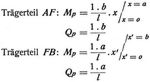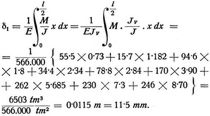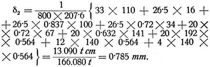- Durchbiegung
Durchbiegung (sagging or hogging; flexion; flessione) im weiteren Sinne die Größe der infolge von Krafteinwirkungen bei einem (stab- oder plattenförmigen) Körper sich ergebenden Änderung des Abstands seiner Punkte von einer Geraden oder Ebene, die man sich durch bestimmte Stützpunkte des Körpers gelegt denkt; D. im engeren Sinn, Einbiegung, auch Einsenkung, ist das Maß der senkrechten Verschiebungen, die einzelne Punkte der Längsachse eines stabförmigen Trägers erleiden, wenn dieser auf zwei oder mehr als fest vorausgesetzten Stützpunkten aufliegt und entweder bloß durch sein eigenes Gewicht, oder noch durch äußere Kräfte oder Lasten beansprucht wird.
Die durch den Einfluß einer Last hervorgerufene D. verschwindet nach Aufhören der Kraft (nach der Entlastung) entweder ganz oder nur teilweise. Die wieder verschwindende Änderung nennt man die elastische, die andere die bleibende (permanente) D.
Bei den Probebelastungen von Baukonstruktionen, hauptsächlich von Eisenbrücken (s. Brückenprobe), wird nach Messung der gesamten D. die Probelast wieder entfernt und die bleibende D. bestimmt. Der Unterschied der beiden D. gibt sodann die elastische, die mit der gerechneten in Vergleich gebracht wird und nicht zu sehr davon abweichen soll. Die bleibende D. soll in der Regel nicht mehr als 1/5000 der Stützweite betragen. Bleibende D. sollen nur bei der erstmaligen Belastung auftreten und nur von der unvermeidlichen Unvollkommenheit der Anarbeitung, nicht aber von einer Überanstrengung der Tragkonstruktion über die Elastizitätsgrenzen hinaus herrühren.
Die Umstände, die auf das Maß der D. Einfluß haben, sind: die Größe der einwirkenden Kräfte, die Länge und die Ausbildung des Trägers (vollwandig, gegliedert, Querschnittsform), ferner die Art der Auflagerung (frei aufliegend oder mit den Enden eingespannt) und schließlich die Formänderungszahl des Trägermaterials.
D. vollwandiger Träger.
Im allgemeinen wirken auf einen Querschnitt eines solchen Trägers ein Biegungsmoment, eine Querkraft, eine Achsial- oder Längskraft und der Einfluß der Temperatur. In der Regel treten bei solchen Tragwerken keine Längskräfte auf, und auch der Einfluß der Querkräfte auf die Größe der D. ist ein sehr kleiner, so daß dieser Einfluß meist vernachlässigt werden kann, insbesondere wenn die Querschnittsabmessung gegenüber der Bauwerksabmessung klein ist. Die Ermittlung der D. kann auf rechnerischem und zeichnerischem Wege erfolgen.
A. Rechnerische Ermittlung der D.
1. Durch unmittelbares Verfolgen der elastischen Formänderung auf Grund des Hookeschen Gesetzes;
2. durch die Anwendung der Gesetze über die Formänderungsarbeit.
Bei ersterem Verfahren wird der Einfluß jeder einzelnen Kraftwirkung gesondert ermittelt, während sich beim zweiten Verfahren eine gemeinschaftliche Behandlung aller Kraftwirkungen erreichen läßt, die in vielen Fällen eine bedeutende Vereinfachung der Rechnung ermöglicht.
Zu 1. Formänderung auf Grund des Hookeschen Gesetzes. Mit Vernachlässigung des Einflusses der Längskräfte und der Temperaturwirkung möge nur der Einfluß der Biegungsmomente und der Querkräfte behandelt werden.
a) D. infolge Biegungsmomente.
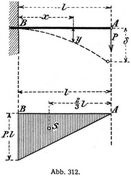
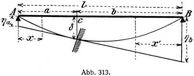
Aus der Gleichung der Biegungslinie d2y/dx2 = M/EJ ergibt sich, daß dieselbe als Seillinie aufgefaßt werden kann, deren Polentfernung EJ und deren Belastungsfläche die Momentenfläche ist (Satz von Mohr). Ein wagrecht eingespannter Kragträger sei an seinem freien Ende mit einer Einzellast P belastet (Abb. 312).
Die Momentenfläche M ist ein Dreieck mit der Fläche
Die größte D. tritt am freien Ende A auf, und ist die über AB schraffierte Momentenfläche als Belastungsfläche anzusehen. Sodann ist
und gemäß dem Satze, daß die Senkrechte an einer Stelle zwischen Seilpolygon und Schlußlinie, mit der Polentfernung multipliziert, das Moment an dieser Stelle gibt M1 = δ. EJ, d.h. δ = M1/EJ = Pl3/3EJ.
Hat man es mit anderen Trägerarten zu tun, so greift man zur Berechnung der D. auf den Kragträger zurück. Liegt z.B. ein beiderseits frei aufliegender Träger mit veränderlichem Trägheitsmomente vor und es sei im Querschnitt C in den Entfernungen a und b von den Stützen A und B die D. δ zu rechnen, so denkt man sich an die Biegungslinie unter C eine Tangente gezogen, den frei aufliegenden Träger gewissermaßen in zwei Kragträger AC und BC zerlegt (Abb. 313). Die Abschnitte dieser Tangente an der Stützenvertikalen ergeben sich somit mit
wobei x von A, x‵ von B zu rechnen sind
wobei M das durch irgendeinen Belastungszustand hervorgerufene Moment, J das allgemein veränderliche Trägheitsmoment des frei aufliegenden Trägers bedeuten. Trägt man nun in der Momentenfläche statt der Ordinaten M die jeweilige Größe M/J als Ordinaten auf, so erhält man die verzerrte Momentenfläche und es stellt in der früheren Gleichung für δ das erste Integral das statische Moment der verzerrten Momentenfläche im Trägerteile AC in bezug auf die linke Stützenvertikale, das zweite Integral das statische Moment der verzerrten Momentenfläche des Trägerteiles BC auf die rechte Stützen vertikale dar (s. das Beispiel eines Blechträgers).
Träger mit konstantem Querschnitt.
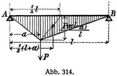
Ein auf zwei Stützen frei aufliegender Träger durch eine Einzellast belastet (Abb. 314).
Die einfache Momentenfläche ist hier
Ihr Schwerpunkt liegt von A entfernt um
Wird diese Momentenfläche als Belastung angesehen, so ergibt sich dafür der Auflagerdruck in B
und das Moment für die Mitte
demnach die D. in der Trägermitte
Unter der Last wird die D.
für a = l/2 ist
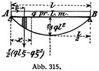
Ein auf zwei Stützpunkten frei aufliegender Träger mit gleichförmig verteilter Last q pro Längenmeter belastet (Abb. 315).
Das Moment der als Belastung aufgefaßten einfachen Momentenfläche in x wird
und die Senkung
für x = l/2 ist
Bei Trägern, die mit einem Ende eingemauert sind, während das andere frei aufliegt, oder bei welchen beide Enden eingespannt sind, ferner bei Trägern, welche auf mehr als zwei Stützen aufliegen, das ist bei kontinuierlichen Trägern, entstehen an den Einspannungsstellen, bzw. an den Zwischenstützen ebenfalls Momente, welche bei Bestimmung der Belastungsfläche für die elastische Linie zu berücksichtigen sind, u. zw. im Sinn ihrer Drehungen.
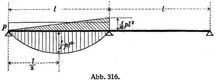
Ein Träger ruhe auf drei Stützen frei auf (kontinuierlicher Träger mit zwei Feldern) und eine Öffnung sei mit p pro Längenmeter gleichmäßig belastet (Abb. 316).
Das Moment für den einfachen Träger ist 1/8 pl2.
An der Mittelstütze entsteht ein entgegengesetztes Moment 1/16 pl2. Die Momentenfläche ist ein Dreieck mit der Fläche
Das zweite Moment für den freien Träger ist
und die Senkung
Für den einfachen Träger ist die Senkung, wie früher gezeigt wurde,
daher für den kontinuierlichen Träger
Für x = l/2 ist
Das Verhältnis der D. des einfachen Trägers zum kontinuierlichen (bei zwei Feldern) mit derselben Stützweite ist also 5 : 7/2 = 10 : 7, d.h. der kontinuierliche Träger hat 7/10 der Biegung des einfachen Trägers.
b) D. infolge der Wirkung der Querkräfte.
Unter der Wirkung eines Biegungsmomentes werden zwei unendlich benachbarte Stabquerschnitte gegeneinander verdreht, während unter der Einwirkung einer Querkraft eine Verschiebung des einen Querschnittes gegenüber dem anderen entsteht. Diese Verschiebung rechnet sich aus:
worin bedeuten: Q die Querkraft, F den Trägerquerschnitt, G den Elastizitätskoeffizienten für Schub- oder Gleitungskoeffizienten
k eine für einen bestimmten Querschnitt konstante Größe. (Für ein Rechteck 5/6, für den Kreis 9/10 für ein
 Profil k = h∙d / f, worin h . d die Fläche des Steges und f die ganze Querschnittsfläche des Profilträgerquerschnittes bedeuten.)
Profil k = h∙d / f, worin h . d die Fläche des Steges und f die ganze Querschnittsfläche des Profilträgerquerschnittes bedeuten.)Zu 2. Rechnerische Ermittlung der D. durch die Anwendung der Arbeitsgesetze.
Unter der Annahme, daß man es mit festen, unelastischen Stützen zu tun hat, wie das in der Regel der Fall ist, daß weiter bei einem Vollwandträger keine Achsialkräfte auftreten und der Einfluß der Temperatur gesondert betrachtet wird, lautet die Gleichung der Verschiebungsarbeit:
Um nun die D. δ an einem bestimmten Querschnitte n zu ermitteln, wird die Kraft 1 am Orte n in der Richtung von δ, also bei der D. vertikal wirkend angenommen. Dieser Kraft P = 1 entsprechen die Größen Qp, MP, und die Arbeitsgleichung lautet unter den früher genannten Annahmen.
Auch aus der Gleichung für die Formänderungsarbeit läßt sich die D. berechnen, da ja der partielle Differentialquotient der Formänderungsarbeit nach der Kraft Pn, welche nur in dem Querschnitt n, wo δ zu suchen ist, im Sinne von δ wirkend gedacht wird, gleich dem Wege also der D. δn sein muß.
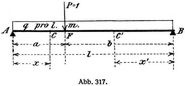
Ein frei aufliegender Träger von konstantem Querschnitt mit festen, unnachgiebigen Stützen sei gleichmäßig mit q auf die Längeneinheit belastet. Es ist die D. des Querschnittes F in der Entfernung a von der linken Stütze zu berechnen (Abb. 317). Zu diesem Zwecke denkt man sich die Last P = 1 in F wirksam. Infolge des Belastungszustandes P = 1 in F werden folgende Kräfte hervorgerufen:
Infolge des Belastungszustandes mit q werden folgende äußere Kräfte für einen Querschnitt im Abstand x von der linken Stütze bedingt:
daher
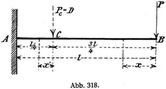
Ein Kragträger von konstantem Querschnitt sei durch eine Einzellast an seinem freien Ende belastet; es ist die D. im ersten Viertel dieses Trägers zu rechnen (Abb. 318).
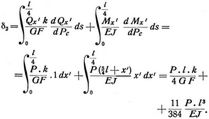
Zu diesem Zwecke muß man eine gedachte Last in C in lotrechtem Sinne wirkend annehmen, Pc, für die Ermittlung der D. aus der Arbeit aber natürlich wieder = 0 setzen. Im Trägerteile BC sind
im Trägerteile CA sind
Die gesamte D. δ = δ1 + δ2, wobei δ1 von dem Trägerteile BC, δ2 vom Trägerteile CA herrührt δ1 = 0, δ = δ2
B. Zeichnerische Ermittlung der D.
Aus der Gleichung der Biegungslinie d2y/dx2 = M/EJ folgt, daß diese als eine Momentenlinie aufgefaßt werden kann, wobei jedes Längenteilchen mit M/EJ belastet gedacht wird. Werden nun die einzelnen Teile der Momentenfläche als Belastungen angesehen, und wird dazu ein Seileck gezeichnet, so ist dieses Seileck unmittelbar die Biegungslinie, wenn die Polweite des Kraftecks mit der Maßeinheit tm × m = tm2 gleich E. J tm2 gewählt wird. Hat man Träger mit veränderlichem J, so nimmt man das Trägheitsmoment eines vorhandenen Querschnittes, meist jenes des stärksten Querschnittes, als Vergleichsträgheitsmoment an, Jv, und hat die Größe M/EJ umzuformen in (1/EJ) ∙ (M Jv/J) so daß man dadurch die verzerrte Momentenfläche erhält und als Polweite im Krafteck H = EJV zu wählen ist. Da EJv in der Regel eine ziemlich große Größe darstellt, wird man als Polweite einen Bruchteil E Jv/n = H nehmen, so daß die Ordinaten der Biegungslinie im n-fachen Maßstabe vergrößert erscheinen.
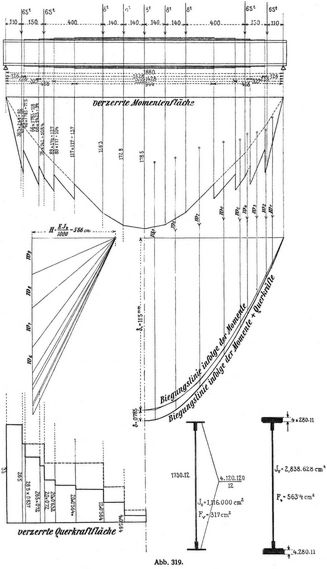
Beispiel. Es soll für den in der Abb. 319 ersichtlichen Blechträger von 18∙8 m Stützweite die größte D. in der Mitte für den Belastungszug nach Norm I der Verordnung des k. k. österr. Eisenbahnministeriums vom 28. August 1904 ermittelt werden.
Als ungünstigste Lastenstellung ergibt sich die in der Abb. 319 ersichtliche und wurde für diese Lastenstellung die Maximalmomentenkurve für Verkehrslast eingezeichnet. Wie aus der Längsansicht zu entnehmen ist, besteht der Träger aus 5 Querschnittstypen. Als Vergleichsträgheitsmoment wird der stärkste Querschnitt in der Trägermitte mit je 4 Lamellen gewählt; hiefür ist Jv = J4 = 2,830.628 cm4, J3 = 2,406.000 cm4, J2 = 1,993.000 cm4, J1 = 1,583.000 cm4, J0 = 1,116.000 cm4 Grundquerschnitt; daher Jv/J3 = 1∙17, Jv/J2 = 1∙42, Jv/J1 = 1∙78, Jv/J0 = 2∙54. Mit diesen Koeffizienten werden die jeweiligen Momentenordinaten multipliziert und man erhält die verzerrte Momentenfläche. Nun werden die Flächeninhalte der einzelnen Streifen der verzerrten Momentenfläche gebildet und als elastische Gewichte in einem Kräfteplane aufgetragen. Bezeichnet man M.Jv/J = w, so sind
Als Polweite im Kräfteplan sollte genommen werden E.JV = 20,000.000 × 0∙0283 tm2 = 566.000 tm2.
Nachdem die elastischen Gewichte wo im Maßstabe 1 cm = 100 tm2 aufgetragen wurden und als Polweite H = 5∙66 cm = 566 tm2 gewählt wurde, so ergeben sich die Ordinaten der zugehörigen Seillinie (Biegungslinie) in 1000facher Vergrößerung gegenüber dem Längenmaßstabe. Die größte Ordinate dieser Biegungslinie unter der Trägermitte ergibt sich mit δ1 = 11∙5 cm = 11∙5 m des Längenmaßstabes = 11∙5/1000 = 11∙5 mm der Wirklichkeit.
Nachdem die Trägerausbildung und die ungünstigste Lastenstellung gegenüber der Mitte eine symmetrische ist, so läßt sich diese D. auch rasch rechnerisch durchführen.
In der Praxis wird vielfach bei solchen Blechträgern die D. infolge der Biegungsmomente gerechnet nach der Formel
worin MP das größte Moment in der Mitte infolge Nutzlast, l die Stützweite des Trägers, J das größte Trägheitsmoment des Querschnittes bedeuten. Hierbei macht man folgende Vernachlässigungen gegenüber dem tatsächlichen Bestande. Man nimmt als Momentenlinie eine Parabel, deren Scheitelordinate gleich dem größten Moment infolge Einzellasten ist, denkt sich also eine äquivalente, gleichförmig verteilte Belastung und berücksichtigt weiters die schwächeren Querschnitte gegen die Auflager zu nicht. Für unser Beispiel ergäbe sich
daher ein Fehler gegenüber der genauen Ermittlung von rund 1%.
An diesem Beispiel möge gleichzeitig der Einfluß der Querkräfte auf die D. gezeigt werden. Da hier verschiedene Querschnittflächen vorhanden sind, so wird man auch hier einen Querschnitt als Vergleichsfläche annehmen, u. zw. den Grundquerschnitt wählen, da hierfür die Größe
ist. Fv = 317 cm2, F1 = 378∙6 cm2, F2 = 440∙2 cm2, F3 = 501∙8 cm2 und F4 = 563∙4 cm2; Fv/F1 = 0∙837, Fv/F2 = 0∙72, Fv/F3 = 0∙632, Fv/F4 = 0∙564. Die Querkraftordinaten mit diesen Koeffizienten multipliziert, geben die verzerrte Querkraftlinie (Abb. 319).
Nun ist
hierin bedeuten h. d = 207∙6 cm2, G = 0∙4. E = 800 t/cm2, Q1 die Ordinaten der verzerrten Querkraftfläche.
Daher die gesamte D. δ = δ1 + δ2 = 11∙5 + 0∙785 = 12∙285 mm.
Wie zu ersehen ist, beträgt der Einfluß der Querkraft auf die gesamte D. rund 6∙4%.
Durchbiegung von Fachwerksträgern.
Bei der Formänderung von Fachwerken kommt, abgesehen vom Temperatureinfluß, nur die Wirkung von Achsialkräften in Betracht, da in den einzelnen Fachwerksstäben bei Voraussetzung gelenkiger Knotenpunkte keine anderen Kräfte auftreten. Auch hier gibt es zur Ermittlung der D. zwei Wege.
A. Rechnerischer Weg.
In der Praxis wird es sich bei der Ermittlung der D. eines Fachwerkes immer darum handeln, nicht die D. aller Knotenpunkte, sondern eines ganz bestimmten, in der Regel des mittleren Knotenpunktes, zu finden. Hierfür wendet man wieder die allgemeine Gleichung für die Verschiebungsarbeit an. Wird der Einfluß der Temperatur gesondert betrachtet und werden feste, unverschiebliche Stützen vorausgesetzt, so reduziert sich die allgemeine Gleichung auf:
Da im Fachwerk die Achsialkraft N für jeden Stab, in dessen Länge s konstant und durch die Stabkraft S, bzw. S‵ zu ersetzen ist, so lautet die Gleichung
Um nun die Verschiebung irgend eines Knotenpunktes zu finden, wählt man die Kraft P‵ = 1 in jenem Knotenpunkte lotrecht wirkend an, dessen D. (lotrechte Formänderung) gesucht werden soll. Die Arbeitsgleichung lautet dann: 1. δ = ∑ S‵. Δ s. Darin bedeuten S‵ die Stabkräfte, hervorgerufen durch die alleinige Wirkung der Kraft 1 im betreffenden Knotenpunkte, welche am besten mit Hilfe eines Cremonaplanes ermittelt werden; Δ s die Längenänderungen der Stäbe infolge des Belastungszustandes, für den die D. gesucht werden soll, δ die Größe der D.
Hat man nun für alle Knotenpunkte eines Fachwerkes die lotrechten Verschiebungen zu ermitteln, so wird man mit Vorteil einen schnelleren Weg benutzen. Trägt man die lotrechte Verschiebung jedes Knotens als Ordinate von einer wagrechten Linie aus im entsprechenden Sinne auf, so gibt die Verbindung dieser Punkte die Biegungslinie der betreffenden Gurtung. Zur Bestimmung der Biegungslinie muß man die Änderung der von je zwei aufeinanderfolgenden Gurtstäben gebildeten Randwinkel und die Längenänderungen der Gurtstäbe kennen.
a) Änderung der Winkel.
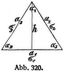
Die Randwinkel setzen sich aus den einzelnen Dreieckswinkeln zusammen, und die Summe der einzelnen Änderungen dieser Dreieckswinkel gibt die Änderung des betreffenden Randwinkels. Wenn in einem Dreieck (Abb. 320) a1, a2, a3 die Seiten und α1, α2, α3 die gegenüberliegenden Winkel bezeichnen und σ1, σ2, σ3 die Spannungen der Stäbe a1, a2, a3, so ergibt sich die Änderung des Winkels α1 mit:
Δ α1 = 1/E [(σ1 – σ2) cotg α3 + (σ1 – σ2) cotg α2],
mit welcher Gleichung alle die Änderungen der einzelnen den Gesamtrandwinkel bildenden Dreieckswinkel gerechnet werden können.
b) Längenänderungen der Gurtstäbe.
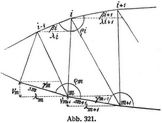
α) Untergurte (Abb. 321).
Zwei aneinander stoßende Gurtstäbe sm und sm + 1 haben eine vertikale Projektion νm und vm + 1 und eine horizontale λm und λm + 1, die Winkel dieser Gurtstäbe gegen die Wagrechte sind γm und γm + 1 (positiv, wenn der Gurtstab unter der Wagrechten, welche durch das linke Stabende gezogen wird, liegt).
Die Senkungen der Knotenpunkte seien δm und δm + 1.
Dann ist
wobei
Faßt man die Ausdrücke
als Einzellasten auf, welche in den Knotenpunkten eines einfachen Trägers wirken, so gibt das mit diesen Einzellasten gezeichnete Momentenvieleck das Biegungsvieleck der unteren Gurtung.
β) Für die obere Gurtung erhält man ähnlich die Gleichung
Treten am ersten und letzten Knotenpunkt senkrechte Verschiebungen auf, so sind diese als Ordinaten in dem gezeichneten Momentenvieleck nach aufwärts aufzutragen und gibt die Verbindungslinie die Schlußlinie, von welcher die senkrechten Abstände des Vielecks an den Knoten zu messen sind.
Bei Fachwerken (wo eine Lage der Streben senkrecht ist) kann das Biegungsvieleck der oberen Gurtung leicht gefunden werden, indem man von der Senkung der unteren Knotenpunkte die Änderung der entsprechenden Vertikalen abzieht, d.h. δ0 = δu – Δ h.
B. Zeichnerischer Weg.
Hierbei kann man sich zweier Methoden bedienen:
1. Die Ermittlung der Biegelinie mit Hilfe eines aus den elastischen Gewichten der Winkeländerungen gezeichneten Krafteckes.
2. Die Ermittlung der Biegelinie aus den Verschiebungsplänen, auch Williotsches Verfahren benannt.
Zu 1. Bei der zeichnerischen Ermittlung der Winkeländerungen muß man alle Randwinkel im Zuge des Ober- oder Untergurtes berücksichtigen, je nachdem für welche Knotenpunkte die D. gesucht werden soll. Alle Änderungen dieser Randwinkel setzen sich aus den Änderungen der Einzelwinkel zusammen.
Die Winkeländerung kann nach verschiedenen Verfahren zeichnerisch ermittelt werden. Ein Verfahren besteht in folgendem:
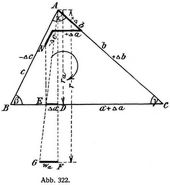
Sind die Längen der Dreieckseiten abc, die Winkel α, β, γ und die drei Höhen ra, rb, rc, so lassen sich die einzelnen Seiten als trigonometrische Funktionen der Winkel und anderen Dreieckseiten ausdrücken. a = b. cos γ + c. cos β (Abb. 322) α + β + γ = π; durch totale Differenzierung der ersten Gleichung erhält man Δa = Δ b. cos γ + Δ c. cos β – b. sin γ Δ – c. sin β. Δ β. Ferners muß Δ α + Δ β+ Δ γ = 0 und b. sin γ = c sin β = ra, daher
Δa = Δ b. cos γ + Δ c cos β + ra Δ α., und
der Zähler dieses Ausdruckes stellt vor die Projektion der algebraischen Summe der Längenänderungen aller drei Dreieckseiten auf die Seite a; Δα = Δa‵/ra. Zur Konstruktion dieses Ausdruckes geht man so vor, daß man von dem Eckpunkte des Dreieckes ausgeht, dessen Winkeländerung ermittelt werden soll, etwa A (Abb. 322), umfährt den Dreiecksumfang im Sinne des Uhrzeigers und reiht nun die Längenänderungen der einzelnen Stäbe durch Einzeichnen von Parallelen zu den betrachteten Seiten derart aneinander an, daß man Verlängerungen als + Werte in demselben Umfahrungssinne (Δa, Δb), Verkürzungen als (–) Werte im entgegengesetzten Umfahrungssinne aufträgt (Δc), in welchem man die angehörigen Seiten durchfährt. Dadurch erhält man einen Endpunkt N. Diesen Endpunkt projiziert man auf die Seite a und erhält den Punkt E. Es stellt daher DE = a‵ die Projektion der algebraischen Summe der Längenänderungen aller drei Seiten auf a vor. Diese Größen sind + oder (–), wenn sie sich, von A aus betrachtet, von den Fußpunkten der Höhen aus nach rechts oder links erstrecken. In unserem Falle ist Δa positiv. Da nun für die verschiedenen Dreieckswinkel auch verschieden große Höhen vorliegen, so bringt man sämtliche Winkeländerungen auf eine gemeinsame Grundlänge r, um die dadurch ermittelten Größen gleich als elastische Gewichte in das Krafteck übertragen zu können. Man trägt daher auf allen Dreieckshöhen ein und dasselbe Maß r auf, etwa AF = r, verbindet A mit dem Endpunkte E von Δa‵ und errichtet in F eine Parallele zu a. F G ∥ B C; daher Δa‵/ra = wa/r. Mit diesen Größen w zeichnet man wieder ein Krafteck, wählt eine Polweite H und zeichnet dazu die Seillinie. Die Ordinaten dieser Seillinie müssen dann noch mit H/r multipliziert werden, wobei r und die Ordinaten im Längenmaßstab abzugreifen sind. Es ist daher vorteilhaft für die Polweite H, ein Vielfaches von r zu wählen. Diese nach diesem Verfahren ermittelte Seillinie stellt aber erst den Einfluß der Winkeländerungen dar. Zu diesen Seillinienordinaten ist noch der Einfluß der Stablängenänderungen des betrachteten Stabzuges hinzuzufügen; denn das in den Knotenpunkten anzubringende gesamte elastische Gewicht rechnet sich nach früherem
Diesen zweiten Einfluß ermittelt man sich mittels eines Verschiebungsplanes, hat aber dann die dadurch ermittelten lotrechten Verschiebungen immer in entsprechendem Maßstabe den Ordinaten der ursprünglichen Seillinie hinzuzufügen.
Ist der betrachtete Gurt wagrecht, so sind alle Winkel β der früheren Gleichung Null, d.h. in diesem speziellen Falle entfällt dieser zweite Einfluß und die ursprüngliche Seillinie ist schon die Biegungslinie des betrachteten Gurtes (s. späteres Beispiel).
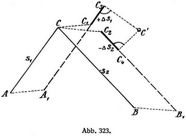
Zu 2. Ermittlung der D. aus den Williotschen Verschiebungsplänen. Dieses Verfahren beruht auf folgender Überlegung. Denkt man sich einen Punkt C durch 2 Stäbe s1 und s2 mit 2 anderen Punkten A und B festgehalten, und würden sich die Endpunkte A und B nach A1 und B1 verschieben, so müßten die Stäbe s1 und s2 parallel zu ihrer ursprünglichen Lage nach A1 C1 und B1 C1 zu liegen kommen, falls eine Längenänderung dieser Stäbe nicht eintreten würde (Abb. 323), A1 C1 || AC, B1 C2 || BC. Erleiden nun diese Stäbe Längenänderungen, etwa Stab s1 als gezogen + Δs1, Stab s2 als gedrückt – Δs2, so fallen die Endpunkte C1 nach C3 und C2 nach C4, so daß der Stab s1 gegeben ist durch A1 C3, der Stab s2 durch B1 C4. Diese ideal gedachten Punkte C3 und C4 müssen aber nach der Formänderung zusammenfallen, da das Dreieck ein geschlossenes sein muß. Es müssen daher beide Stäbe A1 C3 und B1 C4 so weit gedreht werden, bis C3 und C4 im Punkte C1 zusammenfallen. C3 bewegt sich auf einem Kreisbogen, dessen Mittelpunkt A1 ist, C4 auf einen Kreisbogen mit dem Mittelpunkt B1. Da nun diese Verschiebungen tatsächlich sehr kleine Größen vorstellen, so kann man die Kreisbogen durch die Senkrechten auf die Stabrichtungen ersetzen, in deren Schnittpunkte die wirkliche Lage des Punktes C1 nach der Formänderung sich befindet.
Liegt nun ein Fachwerksträger vor, so wiederholt man dieses Verfahren durch Aneinanderreihung für sämtliche Dreicke des Fachwerkes, wobei man vorerst einen beliebigen, zweckmäßig einen mittleren Stab des Fachwerkes festhält. Dadurch erhält man den sog. ersten Verschiebungsplan. Diese so erhaltene Verschiebung des Fachwerkes wäre jene, wenn der beliebig gewählte Stab festgehalten gedacht wäre. Dies ist nun nicht der Fall. Bei den gewöhnlichen frei aufliegenden Fachwerksträgern wird nur ein Knotenpunkt, jener am festen Auflager, tatsächlich festgehalten, während die Verschiebungsrichtung des Knotenpunktes am beweglichen Auflager durch die Bewegungsrichtung der Rollen (gewöhnlich horizontal) bedingt ist. Man muß daher zu der zunächst angenommenen Verschiebung des ganzen Fachwerkes noch eine Drehung um das feste Auflager vornehmen, wobei die Bewegungsrichtung des beweglichen Auflagers vorgeschrieben erscheint. Infolge dieser kleinen Drehbewegung beschreibt jeder Knotenpunkt im ersten Verschiebungsplane einen Weg senkrecht zu seiner Verbindung mit dem festen Auflagerknoten, und die Wege der Knotenpunkte verhalten sich wie ihre Abstände vom festen Knotenpunkte. Der die Drehbewegung darstellende 2. Verschiebungsplan muß daher der Fachwerksfigur ähnlich und um 90° gegen dieselbe verdreht sein. Die Größe dieses zweiten Verschiebungsplanes folgt aus der Bedingung, daß die aus der Drehbewegung des beweglichen Auflagerknotens und der zunächst angenommenen Verschiebung im ersten Verschiebungsplane zusammengesetzte wirkliche Verschiebung des beweglichen Auflagerknotens in die Parallele zur Gleitlagerrichtung fallen muß. Aus diesen beiden Verschiebungsplänen kann man nun sofort die Biegungslinie der Gurte einzeichnen.
Da die Figur des zweiten Verschiebungsplanes jener des Fachwerkes ähnlich und um 90° verdreht ist, so müssen die Projektionen der Punkte des zweiten Verschiebungsplanes auf die Lotrechten der entsprechenden Punkte der Fachwerksfigur eine Gerade bilden, welche bereits die Schlußlinie des Biegungsvieleckes darstellt. Die einzelnen Punkte der Biegungslinie findet man durch Projizieren der Punkte des ersten Verschiebungsplanes in die Lotrechten der entsprechenden Punkte der Fachwerksfigur. Die Ordinaten dieser Biegungslinie sind in demselben Maßstabe abzugreifen, in welchem die elastischen Größen im ersten Verschiebungsplane aufgetragen wurden (siehe folgendes Beispiel).
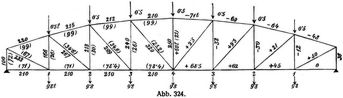
Beispiel: Ein Halbparabelträger mit der Stützweite 16∙8 m sei in den oberen Knotenpunkten mit 0∙5t, in den unteren mit 9∙8t belastet.
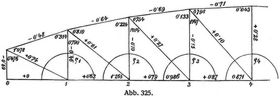
In Abb. 324 sind die in der linken Hälfte eingeschriebenen Zahlen die Längen der einzelnen Stäbe und die eingeklammerten Zahlen die Querschnittsflächen; die Zahlen in der rechten Hälfte geben die Größe der auftretenden Stabkräfte. In Abb. 325 sind in den Dreieckswinkeln die Kotangenten dieser Winkel eingeschrieben, während die anderen Zahlen die Spannungen in t/cm2 angeben.
Die Senkungen der unteren Knotenpunkte sollen bestimmt werden. 1. Auf rechnerischem Wege mittels des Winkeländerungsverfahrens. Da der Untergurt gerade ist, so sind die Winkel γ gleich Null und die Grundgleichung heißt pm = – Δ ςm.
Für jeden Knotenpunkt ist daher Δ ς aus der Summe der Änderung der Dreieckswinkel nach der früher abgeleiteten Formel zu bilden und sind die gefundenen Werte als Einzellasten anzusehen, welche ein Momentenvieleck geben, dessen Ordinaten die mit der Formänderungszahl E multiplizierten Einsenkungen sind. Nach Abb. 325 ist:
E . Δ ς1 = (– 0∙50 – 0∙74) . 0∙476 + (– 0∙48 – 0∙74) × 1∙078 + (– 0∙48 + 0∙46) . 0∙314 + (0∙61 + 0∙46 × 0∙79) + (0∙61 – 0∙63) . 1∙265 = – 1∙092
E . Δ ς2 = (– 0∙46 – 0∙61) . 0∙79 + (– 0∙64 – 0∙61) × 0∙81 + (– 0∙64 + 0∙1) . 0∙224 + (0∙27 + 0∙1) × 1∙014 + (0∙27 – 0∙79) . 0∙986 = – 2∙116
E . Δ ς3 = (– 0∙10 – 0∙27) . 1∙014 + (– 0∙69 – 0∙27 × 0∙754 + (– 0∙69 + 0∙15) .0∙133 + (0∙1 + 0∙15) × 1∙147 + (0∙1 – 0∙87) . 0∙871 = – 1∙555
E . Δ ς4 = [(– 0∙15 – 0∙10) . 1∙147 + (– 0∙71 – 0∙1) × × 0∙798 + (– 0∙71 – 0∙28) . 0∙043] . 2 = – 1∙951.
Mit den Einzellasten E. Δ ς1, E. Δ ς2 u.s.w. werden nunmehr die Momente gerechnet, welche die in den betreffenden Knotenpunkten auftretenden Senkungen ergeben.
Nimmt man vorerst die Feldweite = 1 an, so ergeben sich die Vertikalkräfte:
V4 = 1/2 . 1∙951 = 0∙9755
V3 = 0∙9755 + 1∙555 = 2∙5305
V2 = 2∙5305 + 2∙116 = 4∙6465
V1 = 4∙6465 + 1∙092 = 5∙7385
daher:
M1 = 5∙7385
M2 = 5∙7385 + 4∙6465 = 10∙385
M3 = 10∙385 + 2∙5305 = 12∙9155
M4 = 12∙9155 + 0∙9755 = 13∙8910
Für die Formänderungszahl E = 2000 t/cm2 (Schmiedeeisen) und für die bestehende Feldweite λ = 210 cm ist daher
M = E . δ/λ = 2000/210 . δ = 9∙52 δ und daraus
δ = M/9∙52 = 0∙105 M und
δ1 = 5∙7385 × 0∙105 = 0∙60 cm
δ2 = 10∙385 × 0∙105 = 1∙09 cm
δ3 = 12∙9155 × 0∙105 = 1∙36 cm
δ4 = 13∙891 × 0∙105 = 1∙46 cm
In der Praxis wird wohl in der Regel nur die D. des mittleren Knotenpunktes ermittelt. Für diesen Zweck ist es am einfachsten, die Gleichung der Verschiebungsarbeit zu Hilfe zu nehmen.
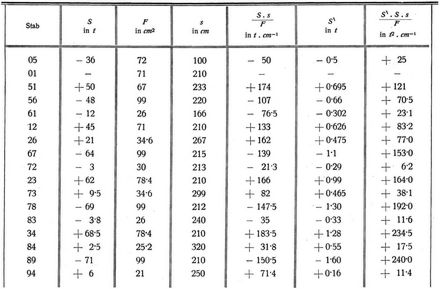
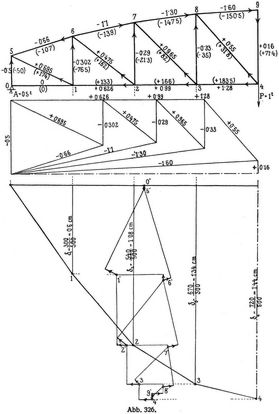
S sind die Stabkräfte, die infolge der Belastung in den Stäben auftreten, S‵ sind die Stabkräfte, die infolge der Belastung P‵ = 1t im Knoten 4 in den Stäben hervorgerufen werden und welche mittels eines Cremonaplanes ermittelt wurden (Abb. 326). Zu diesem Zwecke stellt man immer eine Tabelle auf, wie sie unten angegeben erscheint. In der Abb. 326 bedeuten die nicht eingeklammerten Zahlen die Stabkräfte infolge des Belastungszustandes P‵ = 1 in Knoten 4, während die eingeklammerten Zahlen die E-fachen Längenänderungen der Stäbe in cm bedeuten, die Größen S. s/F infolge des Belastungszustandes, für den die D. bestimmt werden soll.
daher die Gesamtsumme Σ = 1456∙7 + 11∙4
und
Dieselbe Figur wurde auch benutzt, um die Biegungslinie mittels des Williotschen Verschiebungsplanes zu ermitteln. Hierbei wurde zur Bestimmung des ersten Verschiebungsplanes der Mittelstab 49 des ganzen symmetrisch belasteten Fachwerkes festgehalten und die dadurch bedingte Verschiebung des Punktes 8 ermittelt. Dabei wurde vom festgehaltenen Punkte 9‵ die E-fache Längenänderung des Stabes 9 4, als gezogen vom Punkte 9‵ aus nach abwärts aufgetragen 9‵ 4‵. Und zwar wurden im Längenmaßstabe der Zeichnung 4 Einheiten der elastischen Gewichte = 1 cm gemacht. Es müssen daher zum Schlusse die Ordinaten der Biegungslinie, ebenfalls im Längenmaßstabe der Zeichnung (1 : 50) gemessen, multipliziert werden mit 4/E = 4/2000 = 1/500. Sodann wurde vom Punkte 9‵ parallel zu 8 9 die elastische Größe als Druck zum Knoten 9 nach rechts aus aufgetragen und an ihrem Endpunkte eine Senkrechte errichtet. Von 4‵ die Parallelen zu 8 4 und 3 4 gezogen, die elastischen Gewichte im entsprechenden Sinne aufgetragen und die Senkrechten errichtet, so daß im Schnittpunkte der Punkt 8‵ sich nach der Verschiebung ergibt. Dieses Verfahren wurde nun fortgesetzt, bis sich sämtliche Punkte des ersten Verschiebungsplanes 9‵ .... 0‵ ergaben. Da das Fachwerk ganz symmetrisch ausgebildet und auch ganz symmetrisch belastet erscheint, gelangen die Knotenpunkte des festen und des auf einer wagrechten Ebene gleitenden beweglichen Auflagers in ein und dieselbe Höhe, d.h. der zweite Verschiebungsplan wird hier zu Null und die durch 0‵ gezeichnete Wagrechte ist bereits die Schlußlinie des Biegungsvieleckes. Durch Einprojizieren der Punkte des ersten Verschiebungsplanes in die Lotrechte der entsprechenden Punkte des Fachwerkes ergeben sich die Punkte des Biegungsvieleckes. In unserem Falle stellt die gezeichnete Linie die Biegungslinie des Untergurts dar.
Literatur: W. Ritter, Anwendungen der graphischen Statik. Zürich 4 Bände. I, 1888, II, 1890, III, 1900, IV, 1906. – Müller-Breslau, Neuere Methoden der Festigkeitslehre. 3. Aufl. 1904; Die graphische Statik der Baukonstruktionen. I. Bd., 4. Aufl., 1905, II. Bd., 1. Abt., 4. Aufl., 1907, 2. Abt., 1. Aufl. 1908. – Keck-Hotopp, Vorträge über Elastizitätslehre. I. Teil, 2. Aufl., 1905, II. Teil, 2. Aufl., 1908. – Ostenfeld, Technische Statik. 1904. – Mohr, Abhandlungen aus dem Gebiete der technischen Mechanik. 1906. – Handbuch der Ingenieurwissenschaften. II; Der Brückenbau. III. Bd., 4. Aufl., 1909. – Mehrtens, Vorlesungen über Ingenieurwissenschaften. I. Teil, Statik und Festigkeitslehre. I. Bd., 1999, II. Bd., 2. Aufl., 1910. – Otzen-Barkhausen, Zahlenbeispiele zur statischen Berechnung von Brücken und Dächern. 2. Aufl., 1908. – Anhang zu den Zahlenbeispielen. 1. Aufl., 1909. – Otzen, Praktische Winke zum Studium der Statik. 1911. – Foerster, Taschenbuch für Bauingenieure. 1911.
Nowak.
http://www.zeno.org/Roell-1912. 1912–1923.