- Harmonische
-
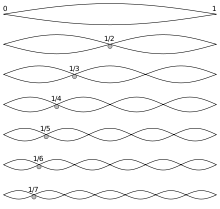
Eine Harmonische ist in der Akustik, der Quantenoptik und Technik ein ganzzahliges Vielfaches einer Grundfrequenz.
Als Funktion der Zeit beschreibt die Harmonische einen rein sinusförmigen Verlauf. Harmonische spielen sowohl in der Musik wie auch in der Mechanik, Elektrotechnik und Optik eine Rolle. In der Musik werden sie meistens mit Oberton bezeichnet, siehe diesen Artikel für anschauliche Beispiele.
Inhaltsverzeichnis
Grundlagen
Mit der FFT und der DFT kann man beliebige periodische Signalverläufe, die z. B. mit einem Musikinstrument als Ton oder einem Oszillator als elektrisches Audiosignal oder sonstiges Signal erzeugt werden, in ihr Frequenzspektrum zerlegen. Dabei zeigt sich, dass sich diese Signale neben dem sinusförmigen Signal mit der Grundfrequenz f praktisch immer zusätzlich aus vielen weiteren sinusförmigen Signalen mit den Frequenzen 2 f, 3 f, 4 f usw. zusammensetzen. Beliebige periodische Signalverläufe erweisen sich so als Summe unendlich vieler sinusförmiger Signale. Technisch kann diese Analyse mit einem Spektrumanalysator durchgeführt werden. In der Praxis kommen nur 'fastperiodische' Harmonische vor bei denen die Kurzzeit-Fourier-Transformation und Wavelet-Transformation vorrangig zum Einsatz kommt.
Bei harmonisch komplexen Tönen stehen die Frequenzen untereinander und zur Grundfrequenz in ganzzahligem Verhältnis. In der Musik werden gleichzeitig erklingende Töne mit solchen Frequenzverhältnissen als harmonischer Klang empfunden. Daher rührt die Bezeichnung im hier beschriebenen allgemeineren Zusammenhang. Bei angenähert harmonisch komplexen Tönen haben höhere Frequenzanteile einen nicht genau ganzzahlige Bezug zur Grundfrequenz und weisen bereits einen nicht zu vernachlässigenden Anteil an Inharmonizität auf. Bei gering harmonische komplexen Tönen weisen Tonsignale Teiltonfrequenzen auf die bereits erheblich vom harmonischen Muster abweichen. Dazu gehören alle Klänge welche durch anschlagen von Glocken Stäben oder Röhren oder membrameartigen Körpern entstehen.
In der Musik ist das Signal ein Klang. Jeder Klang setzt sich aus dem Grundton und den Obertönen zusammen. Hier bestimmen die relativen Stärken, physikalisch die Amplitudenverhältnisse der Obertöne, die Klangfarbe des Tons. Bei Begriffen wie Teiltönen, Partialtönen oder harmonischen Frequenzen wird in der Audiotechnik die Grundfrequenz mitgezählt. Spricht man von Obertönen, wird die Grundfrequenz nicht mitgezählt und nur die Vielfachen der Grundfrequenz betrachtet. In der Literatur finden sich auch noch Bezeichnungen wie Subharmonische Tonreihe, die angelehnt an die mathematischen Definitionen für Subharmonische Funktion zu sehen ist. Im Bereich von Ultraschall spricht man auch noch von Ultraharmonischen.
In der Elektrotechnik und Nachrichtentechnik bestimmt der Anteil an Signalen mit harmonischen Frequenzen, die bei der Durchleitung durch ein System (z.B. Verstärker oder Übertragungsstrecke) zum ursprünglichen Signal dazukommen, wie stark dieses sinusförmige Eingangssignal (mit der Grundfrequenz) bei der Durchleitung verzerrt wird. Diese Verzerrungen werden als Klirrfaktor bewertet. Die dabei entstehenden ganzzahligen Vielfachen der Grundfrequenz werden am Ausgang des Systems der Grundfrequenz überlagert. In der Leistungselektronik bilden die, beispielsweise durch Gleichrichter erzeugten, harmonischen Frequenzen störende Rückwirkungen auf das mit Wechselspannung betriebene öffentliche Versorgungsnetz. Die auftretenden harmonischen Frequenzen oberhalb der Netzfrequenz werden mittels der Leistungsfaktorkorrektur reduziert.
Das Konzept der harmonischen Frequenzen bezieht sich auf abstrakte Signale. Wenn man über die Vorgänge beim Senden des Signals (also Schwingungen) spricht, heißt das entsprechende Konzept Oberschwingung: „Schwingung des Senders mit einer harmonischen (Schwingungs)frequenz“ - nicht zu verwechseln mit harmonische Schwingung. Fasst man den Überträger des Signals, wie Luft für Töne, das elektromagnetische Feld für Funksignale usw., ins Auge, dann spricht man von Oberwellen.
Beispiel: Kammerton a' und die ersten vier Harmonischen
Diese Tabelle zeigt den Grundton a' (das ist der Kammerton mit der Grundfrequenz f = 440 Hz) und seine ersten drei Obertöne mit ihrer jeweiligen Ordnung n und ihren Frequenzen. Die n. Harmonische hat allgemein die Frequenz n·f.
Harmonische Reihe Frequenz 1 · f = 440 Hz 2 · f = 880 Hz 3 · f = 1320 Hz 4 · f = 1760 Hz Ordnung n = 1 n = 2 n = 3 n = 4 Bezeichnung 1 Grundfrequenz 1. Oberton 2. Oberton 3. Oberton Bezeichnung 2 1. Teilton 2. Teilton 3. Teilton 4. Teilton Bezeichnung 3 1. Harmonische 2. Harmonische 3. Harmonische 4. Harmonische Der Grundton ist die 1. Harmonische, eine Oktave darüber ist die 2. Harmonische, was der 1. Oberton ist. Der Oberton ist zahlenmäßig immer um eine Zahl geringer, als es die Harmonische ist. Geradzahlige Harmonische sind ungeradzahlige Obertöne und umgekehrt.
Literatur
- Michael Dickreiter, Volker Dittel, Wolfgang Hoeg, Martin Wöhr, "Handbuch der Tonstudiotechnik", 7. völlig neu bearbeitete und erweiterte Auflage, Herausgegeben von der ARD.ZDF medienakademie, Nürnberg, 2 Bände, Verlag: K G Saur, München, ISBN 3598117655 oder ISBN 978-3-598-11765-7
- Dieter Meschede (Herausgeber): Gerthsen, Physik. Berlin, Springer Verlag, 2004, ISBN 3-540-02622-3
Siehe auch
- Oberton
- Verzerrung (Akustik)
- Flageolettton
- Fourieranalyse
- Vokaldreieck, Vokaltrapez
- Psychoakustik
- Hohe Harmonische
- Multiphotonenmikroskop
Weblinks
 Wiktionary: Harmonische – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Wiktionary: Harmonische – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Wikimedia Foundation.