- Scheinleistung
-
Die Scheinleistung, auch Anschlusswert oder Anschlussleistung, kennzeichnet die einem elektrischen Verbraucher zugeführte oder zuzuführende elektrische Leistung; diese stimmt nicht notwendig mit der vom Verbraucher in Form thermischer, mechanischer oder anderer Energie weitergegebenen Leistung überein. Die Scheinleistung S ergibt sich aus den Effektivwerten von elektrischer Stromstärke I und elektrischer Spannung U und setzt sich zusammen aus der tatsächlich umgesetzten Wirkleistung P und einer zusätzlichen Blindleistung Qtot
Alle drei Leistungsgrößen sind durch Mittelwerte bzw. Integrale definierte Größen. Für sie gibt es bei Stationarität keine von der Zeit abhängigen Augenblickswerte.
Bei verschwindender Blindleistung, wie beispielsweise bei Gleichspannung, ist die Scheinleistung gleich dem Betrag der Wirkleistung, sonst größer. Elektrische Betriebsmittel, die Leistung übertragen, wie Transformatoren oder elektrische Leitungen, müssen entsprechend der zu übertragenden Scheinleistung ausgelegt sein.
Statt der Einheit der Leistung Watt (Einheitenzeichen W) wird für Scheinleistung die Einheit Voltampere (Einheitenzeichen VA) verwendet, für die Blindleistung die Einheit Var (Einheitenzeichen var).
Inhaltsverzeichnis
Scheinleistung bei sinusförmigen Größen
Bei sinusförmigen Größen entsteht Verschiebungsblindleistung Q, wenn die Phasen von Strom und Spannung um einen Winkel φ verschoben sind. Für die Scheinleistung gilt in diesem Fall
mit

und

Wenn ein elektrischer Verbraucher oder ein Versorgungsnetz lineare Induktivitäten oder Kapazitäten enthält, benötigen diese zum Aufbau des magnetischen oder elektrischen Feldes eine elektrische Energie, die jedoch nach jeder halben Periodendauer wieder an das Netz zurückgegeben wird. Der für die Feldenergie erforderliche Blindstrom ist gegenüber der Spannung um eine Viertelperiode bzw. 90° verschoben. Die mit dem Transport der Feldenergie verbundene Blindleistung und die im Verbraucher umgesetzte Wirkleistung ergeben geometrisch addiert die Scheinleistung.
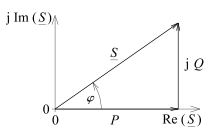 Leistungszeigerdiagramm bei sinusförmigen Größen
Leistungszeigerdiagramm bei sinusförmigen Größen
Das Netz und die Betriebsmittel wie z. B. die versorgenden Generatoren und Transformatoren müssen sämtlich für den Wert der Scheinleistung bemessen werden. Dies gilt nur dann nicht, wenn eine Blindstromkompensation den Blindstrom-Fluss auf die örtlichen verbraucherinternen Leitungsverbindungen begrenzt.
In der komplexen Wechselstromrechnung für den sinusförmigen Spannungs- bzw. Stromverlauf ist die Scheinleistung definiert als Betrag der komplexen Scheinleistung S und als geometrische Summe aus Wirkleistung P und Blindleistung Q. Die komplexe Scheinleistung ist definiert als das Produkt der komplexen Spannung U mit dem konjugiert komplexen Strom I*.
Scheinleistung bei nicht sinusförmigen Größen
Der allgemeine Fall
In einem elektrischen Netzwerk mit verzerrten, d. h. nicht sinusförmigen Spannungen oder Strömen treten Oberschwingungen auf. Jedes periodische Signal lässt sich mittels der Fourieranalyse in eine Reihe von einzelnen Sinusschwingungen, sogenannten Spektralkomponenten, zerlegen. Am Beispiel des Stromes I besteht dieser aus
- der Grundschwingung mit dem Effektivwert I1 und dem Phasenverschiebungswinkel φ1 zur Spannung mit derselben Frequenz
- den Oberschwingungen mit I2 und φ2, I3 und φ3, I4 und φ4 usw.
In diesem Fall lässt sich ein cos φ nicht mehr angeben. An dessen Stelle tritt der Leistungsfaktor

Als Beispiele, in denen die Formeln für Sinusgrößen nicht angewendet werden können, seien genannt:
- Nicht lineare Verbraucher, betrieben an einer sinusförmigen Spannungsquelle. Diese enthalten beispielsweise Gleichrichter, wie sie in Netzteilen zu finden sind. Es treten dabei Verzerrungen auf, welche sich auf die Scheinleistung auswirken.
- Magnetische Kreise mit ferromagnetischem Kernmaterial, das Sättigungs- und Hystereseeffekte zeigt − wie z. B. Spulen oder Transformatoren, die sich insbesondere bei Übersteuerung nicht linear verhalten und den Strom verzerren.
- Phasenanschnittsteuerung mit nach jedem Nulldurchgang verzögertem Einschalten des Stroms. Es kommt zumindest beim Strom zu einer zeitlichen Verschiebung in der Grundschwingung und zur Ausbildung von Oberschwingungen.
Zur weiteren Berechnung müssen die zeitlichen Verläufe oder die Frequenzspektren bekannt sein.
- Im Zeitbereich


- Im Frequenzbereich

Welchen Beitrag die Blindleistung zur Scheinleistung liefert, lässt sich nicht angeben. Nur der Rückschluss über
ist möglich.
Ein Spezialfall
Die Spannung bleibt häufig als eingeprägte Größe trotz nicht linearer Last unverzerrt, also U = U1 . Dann vereinfachen sich die Gleichungen zu
Die Blindleistung lässt sich in diesem Fall angeben als aus zwei Anteilen bestehend (siehe auch Blindleistung)
mit einer Grundschwingungs-Verschiebungsblindleistung
und einer von den Oberschwingungen verursachten Verzerrungsblindleistung
Probleme mit Schaltern
Beispiel: Eine Schaltung bestehe aus einer Quelle mit sinusförmiger Spannung, einem Dimmer und einem ohmschen Verbraucher. Hier müssen getrennt betrachtet werden
- die Leitung zwischen Dimmer und Verbraucher (der Dimmer wird gedanklich der Quelle zugeschlagen) und
- die Leitung zwischen Quelle und Dimmer (der Dimmer wird gedanklich dem Verbraucher zugeschlagen).
Am ohmschen Widerstand R ist jeder Augenblickswert u(t) proportional zu i(t)
Der Strom fließt ab der „Zündung“, also um ein αT verzögert zum Nulldurchgang, bis zum nächsten Nulldurchgang und entsprechend in der zweiten Halbperiode. Eingesetzt in die Gleichungen für den Zeitbereich kommt man auf
und
Also ist hier
 und es gibt keine Verzerrungsblindleistung trotz des verzerrten Stromes. Auf dasselbe Ergebnis kommt man, wenn man beachtet, dass beim ohmschem Verbraucher keine Phasenverschiebung entsteht, dass also für die Gleichungen im Frequenzbereich
und es gibt keine Verzerrungsblindleistung trotz des verzerrten Stromes. Auf dasselbe Ergebnis kommt man, wenn man beachtet, dass beim ohmschem Verbraucher keine Phasenverschiebung entsteht, dass also für die Gleichungen im Frequenzbereich  ist für die Grundschwingung und alle Oberschwingungen.
ist für die Grundschwingung und alle Oberschwingungen.Anders auf der Leitung zwischen Quelle und Dimmer: Hier fließt derselbe „gedimmte“ Strom, aber die Spannung verläuft ungedimmt sinusförmig. Damit hat die Spannung einen höheren Effektivwert, und es entsteht eine höhere Scheinleistung bei unveränderter Wirkleistung. Diese Erhöhung wird als Blindleistung erklärt, die sowohl Verschiebungsblindleistung als auch Verzerrungsblindleistung enthält. Dabei kann die Verschiebungsblindleistung aber nicht als Anzeichen für Rückspeisung gedeutet werden, denn es gibt kein speicherndes Bauteil in diesem Beispiel. Je verzerrter der Strom wird, desto größer wird
 : Mit zunehmender Verzögerung des Zündzeitpunktes im Dimmer wird P immer kleiner, ohne dass − bis T/4 – zugleich der Scheitelwert des Stromes abnimmt.
: Mit zunehmender Verzögerung des Zündzeitpunktes im Dimmer wird P immer kleiner, ohne dass − bis T/4 – zugleich der Scheitelwert des Stromes abnimmt.Siehe auch
Scheinwiderstand, Wirkwiderstand, Blindwiderstand
Nachweis
Mit Ausnahme bei den Problemen mit Schaltern fußt der Artikel auf DIN 40110-1:1994-4 „Wechselstromgrößen; Zweileiter-Stromkreise“
Literaturquellen
- René Flosdorff, Günther Hilgarth: Elektrische Energieverteilung. 9. Auflage. Teubner, 2005, ISBN 3-519-36424-7.
Wikimedia Foundation.














