- Bedingter Erwartungswert
-
Bedingte Erwartungswerte und bedingte Wahrscheinlichkeiten, gegeben eine Zufallsvariable oder Teil-σ-Algebra, stellen eine Verallgemeinerung von bedingten Wahrscheinlichkeiten dar.
Sie spielen eine zentrale Rolle in der Theorie der stochastischen Prozesse und werden unter anderem bei der Formulierung von Martingalen verwendet.
Inhaltsverzeichnis
Interpretation
Die Bildung des bedingten Erwartungswertes ist gewissermaßen eine Glättung einer Zufallsvariablen auf einer Teil-σ-Algebra. σ-Algebren modellieren verfügbare Information, und eine geglättete Version der Zufallsvariable, die schon auf einer Teil-σ-Algebra messbar ist, enthält weniger Information über den Ausgang eines Zufallsexperimentes. Mit der Bildung der bedingten Erwartung geht eine Reduktion der Beobachtungstiefe einher, die bedingte Erwartung reduziert die Information über eine Zufallsvariable auf eine in Hinsicht der Messbarkeit einfachere Zufallsvariable, ähnlich wie als Extremfall der Erwartungswert einer Zufallsvariablen die Information auf eine einzelne Zahl reduziert.
Geschichte
Das in einigen Aspekten sehr alte Konzept (schon Laplace hat bedingte Dichten berechnet) wurde von Kolmogorow 1933 unter Verwendung des Satz von Radon-Nikodym formalisiert. In Arbeiten von Paul Halmos 1950 und Joseph Doob 1953 wurden bedingte Erwartungen auf das heutige allgemeine Setting von Teil-σ-Algebren auf abstrakten Räumen übertragen.[1]
Einleitung
Wenn ein Ereignis B mit P(B) > 0 gegeben ist, gibt die bedingte Wahrscheinlichkeit
 an, wie wahrscheinlich das Ereignis A ist, wenn man Information über das Eintreten von B erhalten hat. Entsprechend gibt der bedingte Erwartungswert
an, wie wahrscheinlich das Ereignis A ist, wenn man Information über das Eintreten von B erhalten hat. Entsprechend gibt der bedingte Erwartungswert ,
,
an, welchen Wert man für die Zufallsvariable Y im Mittel erwartet, wenn man Information über das Eintreten von B erhalten hat. Hierbei ist 1B die Indikatorfunktion von B, d. h. eine Zufallsvariable, die den Wert 1 annimmt, wenn B eintritt, und 0, wenn nicht.
Beispiel: Y ist das Ergebnis beim Werfen eines regelmäßigen Würfels, eine Zahl zwischen 1 und 6. Das Ereignis, dass man eine 5 oder 6 würfelt, bezeichnen wir mit B. Dann ist
 .
.
Dieser elementare Begriff von bedingten Wahrscheinlichkeiten und Erwartungswerten ist jedoch oft nicht ausreichend. Gesucht sind häufig vielmehr bedingte Wahrscheinlichkeiten und bedingte Erwartungswerte in der Form
(a)
 bzw.
bzw.  ,
,-
- wenn man weiß, dass eine Zufallsvariable X einen Wert x hat,
(b)
 bzw.
bzw.  ,
,-
- wenn man den bei (a) gefundenen Wert als Zufallsvariable betrachtet,
(c)
 bzw.
bzw.  ,
,-
- wenn man Information über das Eintreten bzw. Nichteintreten einer Menge (σ-Algebra)
 von Ereignissen hat.
von Ereignissen hat.
- wenn man Information über das Eintreten bzw. Nichteintreten einer Menge (σ-Algebra)
Die Ausdrücke in (b) und (c) sind im Gegensatz zu (a) selbst Zufallsvariablen, da sie noch von der Zufallsvariable X bzw. der Realisierung der Ereignisse in
 abhängen.
abhängen.Die angegebenen Varianten von bedingten Wahrscheinlichkeiten und Erwartungswerten sind alle miteinander verwandt. Tatsächlich genügt es, nur eine Variante zu definieren, denn alle lassen sich voneinander ableiten:
- Bedingte Wahrscheinlichkeiten und bedingte Erwartungswerte beinhalten das gleiche: Bedingte Erwartungswerte lassen sich, genau wie gewöhnliche Erwartungswerte, als Summen oder Integrale aus bedingten Wahrscheinlichkeiten berechnen.[2] Umgekehrt ist die bedingte Wahrscheinlichkeit eines Ereignisses einfach der bedingte Erwartungswert der Indikatorfunktion des Ereignisses: P(A | ...) = E(1A | ...).
- Die Varianten in (a) und (b) sind äquivalent. Die Zufallsvariable P(A | X) weist für das Ergebnis ω den Wert P(A | X)(ω) = P(A | X = X(ω)) auf, d. h. man erhält für P(A | X) den Wert P(A | X = x), wenn man für X den Wert x beobachtet. Umgekehrt kann man, wenn P(A | X) gegeben ist, immer einen von x abhängigen Ausdruck P(A | X = x) finden, so dass diese Beziehung erfüllt ist.[3] Entsprechendes gilt für bedingte Erwartungswerte.
- Die Varianten in (b) und (c) sind ebenfalls äquivalent, weil man
 als die Menge aller Ereignisse der Form
als die Menge aller Ereignisse der Form  wählen kann (die von X erzeugte σ-Algebra σ(X)), und umgekehrt X als die Familie
wählen kann (die von X erzeugte σ-Algebra σ(X)), und umgekehrt X als die Familie  .[4]
.[4]
Diskreter Fall
Wir betrachten hier den Fall, dass P(X = x) > 0 für alle Werte x von X gilt. Dieser Fall ist besonders einfach zu behandeln, weil die elementare Definition uneingeschränkt anwendbar ist:
Die Funktion
 (wobei
(wobei  das Argument bezeichnet) besitzt alle Eigenschaften eines Wahrscheinlichkeitsmaßes, es handelt sich um eine sogenannte reguläre bedingte Wahrscheinlichkeit. Die bedingte Verteilung
das Argument bezeichnet) besitzt alle Eigenschaften eines Wahrscheinlichkeitsmaßes, es handelt sich um eine sogenannte reguläre bedingte Wahrscheinlichkeit. Die bedingte Verteilung  einer Zufallsvariable Y ist daher ebenfalls eine ganz gewöhnliche Wahrscheinlichkeitsverteilung. Der Erwartungswert dieser Verteilung ist der bedingte Erwartungswert von Y, gegeben X = x:
einer Zufallsvariable Y ist daher ebenfalls eine ganz gewöhnliche Wahrscheinlichkeitsverteilung. Der Erwartungswert dieser Verteilung ist der bedingte Erwartungswert von Y, gegeben X = x:Beispiel
X und Y seien die Augenzahlen bei zwei unabhängigen Würfen mit einem regelmäßigen Würfel und Z = X + Y die Augensumme. Die Verteilung von Z ist gegeben durch
 , z = 2,...,12. Wenn wir aber das Ergebnis X des ersten Wurfs kennen und wissen, dass wir z. B. den Wert 4 gewürfelt haben, erhalten wir die bedingte Verteilung
, z = 2,...,12. Wenn wir aber das Ergebnis X des ersten Wurfs kennen und wissen, dass wir z. B. den Wert 4 gewürfelt haben, erhalten wir die bedingte Verteilung .
.
Der Erwartungswert dieser Verteilung, der bedingte Erwartungswert von Z, gegeben X = 4, ist
 .
.
Allgemeiner gilt für beliebige Werte x von X
 .
.
Wenn wir für x den Wert von X einsetzen, erhalten wir den bedingten Erwartungswert von Z, gegeben X:
 .
.
Dieser Ausdruck ist eine Zufallsvariable; wenn das Ergebnis ω eingetreten ist, weist X den Wert X(ω) auf und E(Z | X) den Wert
 .
.
Satz über die totale Wahrscheinlichkeit
Die Wahrscheinlichkeit eines Ereignisses A lässt sich durch Zerlegen nach den Werten x von X berechnen:
Allgemeiner gilt für jedes Ereignis
 in der σ-Algebra σ(X) die Formel
in der σ-Algebra σ(X) die Formel .
.
Mithilfe der Transformationsformel für das Bildmaß erhält man die äquivalente Formulierung
 .
.
Allgemeiner Fall
Im allgemeinen Fall ist die Definition weit weniger intuitiv als im diskreten Fall, weil man nicht mehr voraussetzen kann, dass die Ereignisse, auf die man bedingt, Wahrscheinlichkeit > 0 haben.
Ein Beispiel
Wir betrachten zwei unabhängige standardnormalverteilte Zufallsvariablen X und Y. Ohne große Überlegung kann man auch hier den bedingten Erwartungswert, gegeben X, der Zufallsvariable Z = 2X + Y − 3 angeben, d. h. den Wert, den man im Mittel für den Ausdruck 2X + Y − 3 erwartet, wenn man X kennt:
- E(Z | X) = 2X − 3 bzw. E(Z | X = x) = 2x − 3
Wie zuvor ist E(Z | X) selbst eine Zufallsvariable, für deren Wert nur die von X erzeugte σ-Algebra σ(X) entscheidend ist. (Setzt man etwa X' = 2X, also σ(X') = σ(X), so erhält man ebenfalls E(Z | X') = E(X' + Y − 3 | X') = X' − 3 = 2X − 3.)
Die Problematik ergibt sich aus folgender Überlegung: Die angegebenen Gleichungen gehen davon aus, dass Y für jeden einzelnen Wert von X standardnormalverteilt ist. Tatsächlich könnte man aber auch annehmen, dass Y im Fall X = 0 konstant den Wert 2 hat und nur in den übrigen Fällen standardnormalverteilt ist: Da das Ereignis X = 0 die Wahrscheinlichkeit 0 hat, wären X und Y insgesamt immer noch unabhängig und standardnormalverteilt. Man erhielte aber E(Z | X = 0) = − 1 statt E(Z | X = 0) = − 3. Das zeigt, dass der bedingte Erwartungswert nicht eindeutig festgelegt ist, und dass es nur sinnvoll ist, den bedingten Erwartungswert für alle Werte von X simultan zu definieren, da man ihn für einzelne Werte beliebig abändern kann.
Der Ansatz von Kolmogorow
Nachdem sich die elementare Definition nicht auf den allgemeinen Fall übertragen lässt, stellt sich die Frage, welche Eigenschaften man beibehalten möchte und auf welche man zu verzichten bereit ist. Der heute allgemein übliche Ansatz, der auf Kolmogorow (1933) zurückgeht[5] und der sich insbesondere in der Theorie der stochastischen Prozesse als nützlich erwiesen hat, verlangt nur zwei Eigenschaften:
(1) P(A | X) soll eine messbare Funktion von X sein. Auf die σ-Algebra
 übertragen bedeutet dies, dass
übertragen bedeutet dies, dass  eine
eine  -messbare Zufallsvariable sein soll.
-messbare Zufallsvariable sein soll.(2) In Analogie zum Satz über die totale Wahrscheinlichkeit soll für jedes
 die Gleichung
die Gleichungerfüllt sein.
Nicht gefordert wird unter anderem
- dass bedingte Wahrscheinlichkeiten eindeutig festgelegt sind,
- dass
 stets ein Wahrscheinlichkeitsmaß ist,
stets ein Wahrscheinlichkeitsmaß ist, - die Eigenschaft P(X = x | X = x) = 1.
Für bedingte Erwartungswerte hat (2) die Formfür alle Mengen
 , für die die Integrale definiert sind. Mit Indikatorfunktionen lässt sich diese Gleichung schreiben als
, für die die Integrale definiert sind. Mit Indikatorfunktionen lässt sich diese Gleichung schreiben als .
.
In dieser Form wird die Gleichung in der folgenden Definition verwendet.
Formale Definition
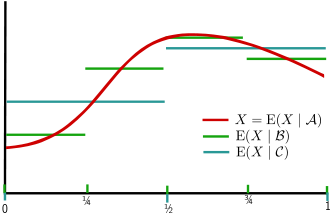 Glättungseigenschaft: P ist hier die Gleichverteilung auf [0,1],
Glättungseigenschaft: P ist hier die Gleichverteilung auf [0,1],
 die von den Intervallen mit Endpunkten 0, ¼, ½, ¾, 1 erzeugte σ-Algebra und
die von den Intervallen mit Endpunkten 0, ¼, ½, ¾, 1 erzeugte σ-Algebra und  die von den Intervallen mit Endpunkten 0, ½, 1 erzeugte σ-Algebra. Die Bildung des bedingten Erwartungswertes bewirkt eine Glättung innerhalb der durch die σ-Algebren beschriebenen Bereiche.
die von den Intervallen mit Endpunkten 0, ½, 1 erzeugte σ-Algebra. Die Bildung des bedingten Erwartungswertes bewirkt eine Glättung innerhalb der durch die σ-Algebren beschriebenen Bereiche.Gegeben sei ein Wahrscheinlichkeitsraum
 und eine Teil-σ-Algebra
und eine Teil-σ-Algebra  .
.(1) X sei eine Zufallsvariable, deren Erwartungswert existiert. Der bedingte Erwartungswert von X, gegeben
 , ist eine Zufallsvariable Z, die die beiden folgenden Bedingungen erfüllt:
, ist eine Zufallsvariable Z, die die beiden folgenden Bedingungen erfüllt:- Z ist
 -messbar und
-messbar und - für alle
 gilt
gilt  .
.
Zwei verschiedene bedingte Erwartungswerte von X gegeben
 („Versionen des bedingten Erwartungswerts“) unterscheiden sich höchstens auf einer (in
(„Versionen des bedingten Erwartungswerts“) unterscheiden sich höchstens auf einer (in  enthaltenen) Nullmenge. Dadurch lässt sich die einheitliche Schreibweise
enthaltenen) Nullmenge. Dadurch lässt sich die einheitliche Schreibweise  für einen bedingten Erwartungswert Z von X gegeben
für einen bedingten Erwartungswert Z von X gegeben  rechtfertigen.
rechtfertigen.Die Schreibweise
 bezeichnet den bedingten Erwartungswert von X, gegeben die von den Zufallsvariablen
bezeichnet den bedingten Erwartungswert von X, gegeben die von den Zufallsvariablen  erzeugte σ-Algebra
erzeugte σ-Algebra  .
.
(2) Die bedingte Wahrscheinlichkeit eines Ereignisses , gegeben
, gegeben  , ist definiert als die Zufallsvariable
, ist definiert als die Zufallsvariable ,
,
d. h. als der bedingte Erwartungswert der Indikatorfunktion von A.
Da die bedingten Wahrscheinlichkeiten verschiedener Ereignisse
verschiedener Ereignisse  somit ohne Bezug zueinander definiert sind und nicht eindeutig festgelegt sind, muss
somit ohne Bezug zueinander definiert sind und nicht eindeutig festgelegt sind, muss  im allgemeinen kein Wahrscheinlichkeitsmaß sein. Wenn dies jedoch der Fall ist, d. h. wenn man die bedingten Wahrscheinlichkeiten
im allgemeinen kein Wahrscheinlichkeitsmaß sein. Wenn dies jedoch der Fall ist, d. h. wenn man die bedingten Wahrscheinlichkeiten  ,
,  zu einem stochastischen Kern π von
zu einem stochastischen Kern π von  nach
nach  zusammenfassen kann,
zusammenfassen kann, für alle
für alle  ,
,
spricht man von regulärer bedingter Wahrscheinlichkeit. Die Berechnung bedingter Erwartungswerte ist dann möglich mithilfe der Formel
 .
.
Faktorisierung: Der bedingte Erwartungswert , der als eine Zufallsvariable (also eine Funktion von ω) definiert ist, lässt sich auch als eine Funktion von
, der als eine Zufallsvariable (also eine Funktion von ω) definiert ist, lässt sich auch als eine Funktion von  darstellen: Es gibt eine messbare Funktion f, so dass
darstellen: Es gibt eine messbare Funktion f, so dass für alle
für alle  .
.
Damit kann man formal auf einzelne Werte bedingte Erwartungswerte definieren:
 .
.
Bei der Verwendung solcher Ausdrücke ist wegen der fehlenden Eindeutigkeit im allgemeinen Fall besondere Vorsicht geboten.
Existenz: Die allgemeine Existenz von bedingten Erwartungswerten für integrierbare Zufallsvariablen (Zufallsvariablen, die einen endlichen Erwartungswert besitzen), also insbesondere von bedingten Wahrscheinlichkeiten, folgt aus dem Satz von Radon-Nikodym; die Definition besagt nämlich nichts anderes, als dass eine Dichte des signierten Maßes ν(B) = E(1BX) bezüglich des Maßes μ(B) = P(B) ist, beide definiert auf dem Messraum
eine Dichte des signierten Maßes ν(B) = E(1BX) bezüglich des Maßes μ(B) = P(B) ist, beide definiert auf dem Messraum  . Die Definition lässt sich noch geringfügig verallgemeinern, so dass man auch Fälle wie E(X | | X | ) = 0 für eine Cauchy-verteilte Zufallsvariable erfassen kann.[2]
. Die Definition lässt sich noch geringfügig verallgemeinern, so dass man auch Fälle wie E(X | | X | ) = 0 für eine Cauchy-verteilte Zufallsvariable erfassen kann.[2]Reguläre bedingte Wahrscheinlichkeiten, auch in faktorisierter Form, existieren in polnischen Räumen mit der Borel-σ-Algebra, allgemeiner gilt: Ist Z eine beliebige Zufallsvariable mit Werten in einem polnischen Raum, so existiert eine Version der Verteilung
 in der Form eines stochastischen Kerns π:
in der Form eines stochastischen Kerns π: für alle
für alle 
Spezialfälle
(1) Für die triviale σ-Algebra
 ergeben sich einfache Erwartungswerte und Wahrscheinlichkeiten:
ergeben sich einfache Erwartungswerte und Wahrscheinlichkeiten: für alle
für alle 
 für alle
für alle 
Entsprechend gilt E(X | Y)(ω) = E(X) und P(A | Y)(ω) = P(A) für alle
 bei Bedingen auf den Wert einer konstanten Zufallsvariable Y.
bei Bedingen auf den Wert einer konstanten Zufallsvariable Y.
(2) Einfache σ-Algebren: Ist mit P(B) > 0, und besitzt B außer sich selbst und der leeren Menge keine Teilmengen in
mit P(B) > 0, und besitzt B außer sich selbst und der leeren Menge keine Teilmengen in  , so stimmt der Wert von
, so stimmt der Wert von  auf B mit der herkömmlichen bedingten Wahrscheinlichkeit überein:
auf B mit der herkömmlichen bedingten Wahrscheinlichkeit überein: für alle
für alle 
Das zeigt, dass die oben aufgeführten Berechnungen im diskreten Fall mit der allgemeinen Definition konsistent sind.
(3) Rechnen mit Dichten: Ist eine beschränkte Dichtefunktion der gemeinsamen Verteilung von Zufallsvariablen X,Y, so ist
eine beschränkte Dichtefunktion der gemeinsamen Verteilung von Zufallsvariablen X,Y, so istdie Dichte einer regulären bedingten Verteilung
 in der faktorisierten Form und für den bedingten Erwartungswert gilt
in der faktorisierten Form und für den bedingten Erwartungswert gilt .
.
(4) Auch in den folgenden Fällen lassen sich reguläre bedingte Verteilungen angeben:- wenn X unabhängig von
 ist, in der Form
ist, in der Form  ,
, - wenn X
 -messbar ist, in der Form
-messbar ist, in der Form  (Diracmaß),
(Diracmaß), - für das Paar (X,Y), wenn X
 -messbar ist, in der Form
-messbar ist, in der Form  , sofern zur Berechnung des Ausdrucks auf der rechten Seite eine reguläre bedingte Verteilung von Y verwendet wird.
, sofern zur Berechnung des Ausdrucks auf der rechten Seite eine reguläre bedingte Verteilung von Y verwendet wird.
Rechenregeln
Alle folgenden Aussagen gelten nur fast sicher (P-fast überall), soweit sie bedingte Erwartungswerte enthalten. Anstelle von
 kann man auch eine Zufallsvariable schreiben.
kann man auch eine Zufallsvariable schreiben.- Herausziehen unabhängiger Faktoren:
- Ist X unabhängig von
 , so gilt
, so gilt  .
. - Ist X unabhängig von
 und von Y, so gilt
und von Y, so gilt  .
. - Sind X,Y unabhängig,
 unabhängig, X von
unabhängig, X von  und Y von
und Y von  unabhängig, so gilt
unabhängig, so gilt 
- Ist X unabhängig von
- Herausziehen bekannter Faktoren:
- Ist X
 -messbar, so gilt
-messbar, so gilt  .
. - Ist X
 -messbar, so gilt
-messbar, so gilt  .
.
- Ist X
- Turmeigenschaft: Für Teil-σ-Algebren
 gilt
gilt  .
.
- Linearität: Es gilt
 und
und  für
für  .
.
- Monotonie: Aus
 folgt
folgt  .
.
- Monotone Konvergenz: Aus
 und
und  folgt
folgt  .
.
- Dominierte Konvergenz: Aus
 und
und  mit
mit  folgt
folgt  .
.
- Lemma von Fatou: Aus
 folgt
folgt  .
.
- Jensensche Ungleichung: Ist
 eine konvexe Funktion, so gilt
eine konvexe Funktion, so gilt  .
.
- Bedingte Erwartungswerte als L2-Projektionen: Die vorherige Eigenschaft impliziert
 , d. h. der bedingte Erwartungswert
, d. h. der bedingte Erwartungswert  ist im Sinne des Skalarprodukts von L2(P) die orthogonale Projektion von X auf den Raum der
ist im Sinne des Skalarprodukts von L2(P) die orthogonale Projektion von X auf den Raum der  -messbaren Funktionen. Die Definition und der Beweis der Existenz der bedingten Erwartung kann über diesen Zugang auch auf der Theorie der Hilbert-Räume und dem Projektionssatz aufgebaut werden.
-messbaren Funktionen. Die Definition und der Beweis der Existenz der bedingten Erwartung kann über diesen Zugang auch auf der Theorie der Hilbert-Räume und dem Projektionssatz aufgebaut werden.
- Martingalkonvergenz: Für eine Zufallsvariable X, die einen endlichen Erwartungswert besitzt, gilt
 , wenn entweder
, wenn entweder  eine aufsteigende Folge von Teil-σ-Algebren ist und
eine aufsteigende Folge von Teil-σ-Algebren ist und  oder wenn
oder wenn  eine absteigende Folge von Teil-σ-Algebren ist und
eine absteigende Folge von Teil-σ-Algebren ist und  .
.
Weitere Beispiele
(1) Wir betrachten das Beispiel aus dem diskreten Fall von oben. X und Y seien die Augenzahlen bei zwei unabhängigen Würfen mit einem regelmäßigen Würfel und Z = X + Y die Augensumme. Die Berechnung des bedingten Erwartungswerts von Z, gegeben X, vereinfacht sich mithilfe der Rechenregeln; zunächst gilt
- E(Z | X) = E(X + Y | X) = E(X | X) + E(Y | X).
Weil X eine messbare Funktion von X ist und Y unabhängig von X ist, gilt E(X | X) = X und E(Y | X) = E(Y). Also erhalten wir
- E(Z | X) = X + E(Y) = X + 3,5.
(2) Wenn X und Y unabhängig und Poisson-verteilt mit Parametern λ und μ sind, dann ist die bedingte Verteilung von X, gegeben X + Y, eine Binomialverteilung: .
.
Hierbei ist
 .
.
(3) Wir betrachten unabhängige exponentialverteilte Zufallsvariablen (oder „Wartezeiten“) T1,...,Tn mit Ratenparametern λ1,...,λn. Dann ist das Minimum T = min(T1,...,Tn) exponentialverteilt mit Parameter λ1 + ... + λn, und für i = 1,...,n gilt fast sicher.
fast sicher.
Einzelnachweise und Anmerkungen
- ↑ Olav Kallenberg: Foundations of Modern Probability, 2. Ausgabe. Springer, New York 2002, ISBN 0-387-95313-2, S. 573.
- ↑ a b Sehr allgemein kann man beispielsweise setzen

 fast überall.
fast überall. - ↑ Diese Faktorisierung ist immer als messbare Funktion möglich. Sie ist im allgemeinen nicht eindeutig, wenn X nicht surjektiv ist.
- ↑ Die mathematische Formulierung geht von folgender Abstraktion des Begriffs „bekannt“ aus: Wenn die Realisation einer Zufallsvariable oder von Ereignissen bekannt ist, ist nicht automatisch jede davon abhängige, sondern nur jede messbar davon abhängige Größe ebenfalls bekannt (oder genauer nur solche, die eine σ-Algebra erzeugen, die eine Teilmenge der anderen ist). In diesem Sinne eignen sich σ-Algebren zur Beschreibung von verfügbarer Information: Die σ-Algebra σ(X) besteht aus den Ereignissen, deren Realisation prinzipiell bekannt ist nach Erhalt der Information über den Wert von X. Die Menge
 wird allgemein als eine σ-Algebra angenommen.
wird allgemein als eine σ-Algebra angenommen. - ↑ A. Kolmogoroff: Grundbegriffe der Wahrscheinlichkeitsrechnung. Springer, Berlin 1933. In der Einleitung des Buches ist die Theorie der bedingten Wahrscheinlichkeiten und Erwartungen als wesentliche Neuerung erwähnt. Für die Definition der bedingten Wahrscheinlichkeit bezüglich einer Zufallsvariable u verwendet Kolmogorow (S. 42) die Gleichung
 , d. h.
, d. h. , die für jede Wahl von A mit
, die für jede Wahl von A mit  erfüllt sein soll (für das Bedingen auf
erfüllt sein soll (für das Bedingen auf  wird die elementare Definition verwendet). Im anschließenden Beweis der Existenz und Eindeutigkeit zeigt Kolmogorow, dass die linke Seite der Gleichung mit
wird die elementare Definition verwendet). Im anschließenden Beweis der Existenz und Eindeutigkeit zeigt Kolmogorow, dass die linke Seite der Gleichung mit  übereinstimmt, die rechte mit
übereinstimmt, die rechte mit  , was den oben angegebenen Ausdrücken entspricht, er arbeitet dann allerdings auf der Ebene des Bildraums von u weiter. Bei bedingten Erwartungen ist die Vorgehensweise ähnlich.
, was den oben angegebenen Ausdrücken entspricht, er arbeitet dann allerdings auf der Ebene des Bildraums von u weiter. Bei bedingten Erwartungen ist die Vorgehensweise ähnlich.
Wikimedia Foundation.






