- Reelle Untermannigfaltigkeit
-
In der Mathematik sind reelle Untermannigfaltigkeiten ein Begriff aus der Analysis und der Differentialgeometrie. Da reelle Mannigfaltigkeiten Teilmengen eines euklidischen Raumes sind, erben sie von diesem viele Eigenschaften wie zum Beispiel die Möglichkeit Abstände zu messen. Jedoch kann man reelle Untermannigfaltigkeit auch als abstrakte differenzierbare Mannigfaltigkeiten (ohne umgebenden Raum) betrachten. Die Äquivalenz der beiden Sichtweisen wird durch den Einbettungssatz von Whitney sichergestellt.
Inhaltsverzeichnis
Untermannigfaltigkeiten des euklidischen Raumes
Ausgewählte Beispiele, in denen Untermannigfaltigkeiten des
 eine Rolle spielen, sind:
eine Rolle spielen, sind:- Optimierung unter Nebenbedingungen
- Mechanische Systeme mit Zwangsbedingungen
- Algebro-Differentialgleichungssysteme bei der numerischen Netzwerkanalyse in der Elektrotechnik
In all diesen Anwendungen wird die Menge der betrachteten Punkte von vornherein auf eine Teilmenge M des
 eingeschränkt, die sich lokal durch Diffeomorphismen auf Gebiete eines
eingeschränkt, die sich lokal durch Diffeomorphismen auf Gebiete eines  mit
mit  abbilden lässt. Diese Teilmenge M wird als m-dimensionale Untermannigfaltigkeit des
abbilden lässt. Diese Teilmenge M wird als m-dimensionale Untermannigfaltigkeit des  bezeichnet. Mit Hilfe der Diffeomorphismen kann man auf der Untermannigfaltigkeit im differentialgeometrischen Sinne genauso rechnen, wie in Gebieten des
bezeichnet. Mit Hilfe der Diffeomorphismen kann man auf der Untermannigfaltigkeit im differentialgeometrischen Sinne genauso rechnen, wie in Gebieten des  .
.Meistens wird die Menge M durch Nebenbedingungen beschrieben. Das heißt, M enthält gerade diejenigen Punkte x, die mit einer vorgegeben stetig differenzierbaren Funktion
 mit 0 < m < n die Gleichung
mit 0 < m < n die Gleichung- f(x) = 0
erfüllen. Außerdem wird noch gefordert, dass 0 ein regulärer Wert von f ist, also die Jacobi-Matrix Df(x) von f für alle Punkte
 den Maximalrang
den Maximalrang  hat.
hat.Die letzte Bedingung sichert die Anwendbarkeit des Satzes über implizite Funktionen. Dieser besagt, dass es zu jedem Punkt
 eine
eine  -Umgebung
-Umgebung  von
von  gibt, in der die Punkte
gibt, in der die Punkte  schon eindeutig durch m Koordinaten parametrisiert sind. Die Abbildung, die
schon eindeutig durch m Koordinaten parametrisiert sind. Die Abbildung, die  auf die zur Parametrisierung benötigten Koordinaten projiziert, ist ein Beispiel für eine Kartenabbildungen und
auf die zur Parametrisierung benötigten Koordinaten projiziert, ist ein Beispiel für eine Kartenabbildungen und  ist das zugehörige Kartengebiet. Da es zu jedem Punkt
ist das zugehörige Kartengebiet. Da es zu jedem Punkt  eine Kartenabbildung gibt, kann man ganz M mit den zugehörigen Kartengebieten überdecken. Eine Menge solcher Karten, mit deren Kartengebieten man M überdecken kann, ist ein Beispiel für einen Atlas.
eine Kartenabbildung gibt, kann man ganz M mit den zugehörigen Kartengebieten überdecken. Eine Menge solcher Karten, mit deren Kartengebieten man M überdecken kann, ist ein Beispiel für einen Atlas.Mit Hilfe der Kartenabbildungen kann man auf M lokal wie im
 rechnen. Das motiviert, dass die natürliche Zahl m Dimension von M genannt wird und M als m-dimensionale Untermannigfaltigkeit des
rechnen. Das motiviert, dass die natürliche Zahl m Dimension von M genannt wird und M als m-dimensionale Untermannigfaltigkeit des  bezeichnet wird.
bezeichnet wird.Beispiel
 Kartengebiete und Projektionen als Kartenabbildungen für die eindim. Einheitssphäre
Kartengebiete und Projektionen als Kartenabbildungen für die eindim. Einheitssphäre
Die Einheitssphäre im
 wird mit der stetig differenzierbaren Funktion
wird mit der stetig differenzierbaren Funktion  durch die Gleichung f(x) = 0 beschrieben. Die Jacobi-Matrix Df(x) = 2xT hat für
durch die Gleichung f(x) = 0 beschrieben. Die Jacobi-Matrix Df(x) = 2xT hat für  mit
mit  ihren Maximalrang eins. Also ist
ihren Maximalrang eins. Also ist  eine
eine  -dimensionale Untermannigfaltigkeit des
-dimensionale Untermannigfaltigkeit des  . In jedem Punkt
. In jedem Punkt  ist mindestens eine Koordinate
ist mindestens eine Koordinate  ungleich Null. Für
ungleich Null. Für  kann man mit
kann man mit  die Menge
die Menge  als Kartengebiet nutzen und für
als Kartengebiet nutzen und für  mit
mit  die Menge
die Menge  . Die Abbildung
. Die Abbildung  eignet sich dann für den ersten Fall mit dem Minus vor der Wurzel und im zweiten Fall mit dem Plus vor der Wurzel als lokaler Flachmacher.
eignet sich dann für den ersten Fall mit dem Minus vor der Wurzel und im zweiten Fall mit dem Plus vor der Wurzel als lokaler Flachmacher.Am einfachsten zu veranschaulichen ist dieses Vorgehen für die eindimensionale Einheitssphäre im
 . Im nebenstehenden Bild sind die vier Kartengebiete als dick durchgezogene Linien eingezeichnet. Die Vereinigung der Kartengebiete überdeckt die gesamte Einheitssphäre, also bilden diese Karten zusammen einen Atlas. Die jeweils zu den Kartengebieten gehörigen Flachmacher sind durch einen kleinen Pfeil angedeutet. Die Bilder der Kartengebiete sind dick gestrichelt.
. Im nebenstehenden Bild sind die vier Kartengebiete als dick durchgezogene Linien eingezeichnet. Die Vereinigung der Kartengebiete überdeckt die gesamte Einheitssphäre, also bilden diese Karten zusammen einen Atlas. Die jeweils zu den Kartengebieten gehörigen Flachmacher sind durch einen kleinen Pfeil angedeutet. Die Bilder der Kartengebiete sind dick gestrichelt.Für die zweidimensionale Einheitssphäre im
 benötigt man schon zwei Koordinaten zur eindeutigen Parametrisierung der Punkte in den Kartengebieten. Zum Beispiel wählt man für
benötigt man schon zwei Koordinaten zur eindeutigen Parametrisierung der Punkte in den Kartengebieten. Zum Beispiel wählt man für  die Menge
die Menge  und als Kartenabbildung ϕ(x) = (x2,x3).
und als Kartenabbildung ϕ(x) = (x2,x3).
Auch das Möbiusband hat lokal Eigenschaften wie ein Gebiet des und soll deshalb auch als zweidimensionale differenzierbare Untermannigfaltigkeit des
und soll deshalb auch als zweidimensionale differenzierbare Untermannigfaltigkeit des  bezeichnet werden können. Wäre das Möbiusband als Urbild eines regulären Wertes einer stetig differenzierbaren Funktion
bezeichnet werden können. Wäre das Möbiusband als Urbild eines regulären Wertes einer stetig differenzierbaren Funktion  darstellbar, so müsste der senkrecht auf M stehende stetige Gradient dieser Funktion überall in eine Richtung zeigen (als z.B. von der Vorderseite wegzeigen). Das geht jedoch nicht, da das Möbiusband keine Vorder- oder Rückseite hat. Deshalb muss die Definition der differenzierbaren Untermannigfaltigkeit des
darstellbar, so müsste der senkrecht auf M stehende stetige Gradient dieser Funktion überall in eine Richtung zeigen (als z.B. von der Vorderseite wegzeigen). Das geht jedoch nicht, da das Möbiusband keine Vorder- oder Rückseite hat. Deshalb muss die Definition der differenzierbaren Untermannigfaltigkeit des  etwas allgemeiner gefasst werden.
etwas allgemeiner gefasst werden.Allgemeine Definition einer Untermannigfaltigkeit des Rn
Eine Menge
 ist eine m-dimensionale k-mal stetig differenzierbare Untermannigfaltigkeit des
ist eine m-dimensionale k-mal stetig differenzierbare Untermannigfaltigkeit des  , wenn es zu jedem Punkt
, wenn es zu jedem Punkt  eine
eine  -Umgebung
-Umgebung  und eine k-mal stetig differenzierbare Funktion
und eine k-mal stetig differenzierbare Funktion  mit regulärem Wert 0 gibt, so dass
mit regulärem Wert 0 gibt, so dass  gilt.
gilt.Wichtige Aussagen
Äquivalent dazu ist: Eine Menge
 ist genau dann eine k-mal stetig differenzierbare Untermannigfaltigkeit des
ist genau dann eine k-mal stetig differenzierbare Untermannigfaltigkeit des  , wenn es zu jedem Punkt
, wenn es zu jedem Punkt  einen lokalen Flachmacher gibt, d.h., zu
einen lokalen Flachmacher gibt, d.h., zu  existieren eine
existieren eine  -Umgebung
-Umgebung  und ein Ck Diffeomorphismus
und ein Ck Diffeomorphismus  mit
mit  für alle
für alle  .
.Eine reguläre Parameterdarstellung ist eine stetig differenzierbare Funktion g, die ein Gebiet Ω des
 in den
in den 
 abbildet und deren Jacobi-Matrix Dg(p) für jeden Parameter
abbildet und deren Jacobi-Matrix Dg(p) für jeden Parameter  den Maximalrang m hat.
den Maximalrang m hat.Ist
 ein lokaler Flachmacher einer Mannigfaltigkeit M, so ist
ein lokaler Flachmacher einer Mannigfaltigkeit M, so ist  eine reguläre Parameterdarstellung, die zumindest den Teil
eine reguläre Parameterdarstellung, die zumindest den Teil  von M parametrisiert. Dabei projiziert
von M parametrisiert. Dabei projiziert  mit
mit  auf die wesentlichen Komponenten des lokalen Flachmachers.
auf die wesentlichen Komponenten des lokalen Flachmachers. Beispiel für eine Immersion, deren volles Bild keine Untermannigfaltigkeit des
Beispiel für eine Immersion, deren volles Bild keine Untermannigfaltigkeit des
 ist
istLokal kann man durch reguläre Parameterdarstellungen auch Mannigfaltigkeiten definieren: Ist
 eine reguläre Parameterdarstellung und
eine reguläre Parameterdarstellung und  beliebig, so existiert eine Umgebung
beliebig, so existiert eine Umgebung  von p, so dass das Bild
von p, so dass das Bild  von Up unter g eine differenzierbare Untermannigfaltigkeit des
von Up unter g eine differenzierbare Untermannigfaltigkeit des  darstellt.
darstellt.Beispiel
Die rechts veranschaulichte Immersion
 mit
mit  ist ein Beispiel dafür, dass die vorstehende Aussage nicht notwendigerweise auf das volle Bild einer Immersion verallgemeinerbar ist (sogar dann nicht, wenn, wie in diesem Beispiel, die Immersion injektiv ist). Die Menge
ist ein Beispiel dafür, dass die vorstehende Aussage nicht notwendigerweise auf das volle Bild einer Immersion verallgemeinerbar ist (sogar dann nicht, wenn, wie in diesem Beispiel, die Immersion injektiv ist). Die Menge  ist lokal um den Punkt (0,0) nicht diffeomorph zu einem Intervall der reellen Achse und stellt somit keine eindimensionale Untermannigfaltigkeit des
ist lokal um den Punkt (0,0) nicht diffeomorph zu einem Intervall der reellen Achse und stellt somit keine eindimensionale Untermannigfaltigkeit des  dar.
dar.Tangentialvektoren/Tangentialraum/Tangentialbündel
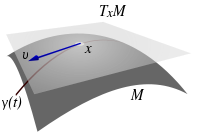
Sei M eine m-dimensionale differenzierbare Untermannigfaltigkeit des
 und
und  . Ein Vektor
. Ein Vektor  heißt Tangentialvektor an M im Punkt x, falls es eine differenzierbare Kurve
heißt Tangentialvektor an M im Punkt x, falls es eine differenzierbare Kurve  mit
mit  und
und  gibt.
gibt.Betrachtet man
 als Bahnkurve eines sich auf der Untermannigfaltigkeit M bewegenden Teilchens, so passiert dieses Teilchen zur Zeit t = 0 den interessierenden Punkt x gerade mit der Geschwindigkeit v.
als Bahnkurve eines sich auf der Untermannigfaltigkeit M bewegenden Teilchens, so passiert dieses Teilchen zur Zeit t = 0 den interessierenden Punkt x gerade mit der Geschwindigkeit v.Die Menge TxM aller Tangentialvektoren an M im Punkt
 ist ein m-dimensionaler linearer Raum und wird als Tangentialraum an M im Punkt x bezeichnet.
ist ein m-dimensionaler linearer Raum und wird als Tangentialraum an M im Punkt x bezeichnet.Definitionsgemäß lässt sich die Untermannigfaltigkeit in einer Umgebung
 des Punktes
des Punktes  als reguläre Nullstelle einer Funktion
als reguläre Nullstelle einer Funktion  darstellen. Sei
darstellen. Sei  eine beliebige stetig differenzierbare Kurve mit
eine beliebige stetig differenzierbare Kurve mit  . Da diese auf der Mannigfaltigkeit verläuft, erfüllt sie die Gleichung f(γ(t)) = 0. Ableiten nach t an der Stelle t = 0 ergibt
. Da diese auf der Mannigfaltigkeit verläuft, erfüllt sie die Gleichung f(γ(t)) = 0. Ableiten nach t an der Stelle t = 0 ergibt  , woraus folgt:
, woraus folgt:Der Tangentialraum TxM ergibt sich gerade als Kern der zu f gehörigen Jacobi-Matrix
 , das heißt, es gilt
, das heißt, es gilt  .
.Hat man eine (lokale) reguläre Parameterdarstellung
 gegeben, die einen Parameterpunkt
gegeben, die einen Parameterpunkt  in
in  abbildet, so lässt sich der Tangentialraum an M in x auch als volles Bild der zugehörigen Jacobi-Matrix Dg(p) darstellen:
abbildet, so lässt sich der Tangentialraum an M in x auch als volles Bild der zugehörigen Jacobi-Matrix Dg(p) darstellen:Die Relation
 , die jedem Punkt
, die jedem Punkt  alle Tangentialvektoren an M in diesem Punkt zuordnet, heißt Tangentialbündel von M.
alle Tangentialvektoren an M in diesem Punkt zuordnet, heißt Tangentialbündel von M.Sei M eine mindestens zweimal stetig differenzierbare Untermannigfaltigkeit des
 und
und  beliebig. Aus einer lokalen Darstellung
beliebig. Aus einer lokalen Darstellung  von M in einer Umgebung
von M in einer Umgebung  von
von  lässt sich eine lokale Darstellung von TM konstruieren:
lässt sich eine lokale Darstellung von TM konstruieren:Damit ist TM eine 2m-dimensionale (mindestens einmal) stetig differenzierbare Untermannigfaltigkeit des
 (im Sinne der üblichen Identifikation des
(im Sinne der üblichen Identifikation des  mit dem
mit dem  ).
).Literatur
- Konrad Königsberger: Analysis 2, Springer-Verlag, Berlin/Heidelberg, 2000, ISBN 3-540-43580-8
Wikimedia Foundation.