- Geschwindigkeit
-
Physikalische Größe Name Geschwindigkeit(1) Formelzeichen der Größe v, u, w, c(2) Größen- und
Einheiten-
systemEinheit Dimension SI Meter pro Sekunde (m·s-1) L·T-1 CGS Zentimeter pro Sekunde (cm·s-1) L·T-1 Planck Lichtgeschwindigkeit (c) c Anmerkungen (1) auch: Bahngeschwindigkeit, Tangentialgeschwindigkeit;
geschlossene Bahn: Umfangsgeschwindigkeit,
Kreis- und Ellipsenbahn: Orbital- oder Umlaufgeschwindigkeit(2) auch vt, v⊥, vu uä.Siehe auch: Winkelgeschwindigkeit,
TangentialbeschleunigungDie Geschwindigkeit (Formelzeichen: v, von lat. Velocitas) beschreibt die Schnelligkeit mit der sich ein Körper bewegt und gibt die innerhalb einer Zeitspanne zurückgelegte Wegstrecke an.
Die zahlenmäßige Erfassung erfolgt allgegenwärtig am Tachometer eines Autos. Die Betrachtung der Geschwindigkeit stellt einen Aspekt der Dynamik und Kinematik dar. Verallgemeinert bezeichnet der Begriff Geschwindigkeit die Änderung einer physikalischen Größe über die Zeit (siehe Änderungsrate).
Definition
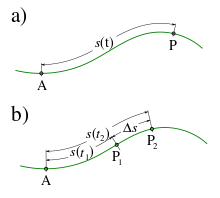
Die entlang einer Bahnkurve vom Ausgangspunkt A zum Zielpunkt P zurückgelegte Wegstrecke trägt die Bezeichnung s. Zusätzlich betrachtet sei die verstrichene Zeit t bis zum erreichen des Punktes P. Der Quotient aus beiden ergibt die Durchschnittsgeschwindigkeit.
Für einen Streckenabschnitt Δs zwischen den Punkten P1 und P2 wird die Zeitspanne Δt benötigt. Hieraus ergibt sich die Durchschnittsgeschwindigkeit im untersuchten Streckenabschnitt.
Durch reduzieren des Beobachtungszeitraum Δt auf einen verschwindend kleinen Zeitintervall entsteht ein Grenzwert den die Mathematik als Differentialquotienten oder Ableitung der Strecke nach der Zeit kennt. Daraus resultiert die Momentangeschwindigkeit.
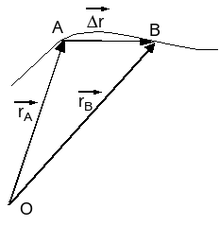
Eine Bewegung im Raum hat einen Verlauf, den man als Bahnkurve bezeichnet und deren Beschreibung durch den Ortsvektor
 als Funktion der Zeit erfolgt. Da jede Ortsänderung eine Richtung aufweist, stellt auch die Geschwindigkeit die diese Änderung im Bezug zur Zeit charakterisiert eine vektorielle Größe dar.
als Funktion der Zeit erfolgt. Da jede Ortsänderung eine Richtung aufweist, stellt auch die Geschwindigkeit die diese Änderung im Bezug zur Zeit charakterisiert eine vektorielle Größe dar.Umgangssprachlich bezieht sich der Ausdruck Geschwindigkeit auf den Betrag der vektoriellen Größe, wofür die Physik den Ausdruck Bahngeschwindigkeit kennt. In der englischen Fachsprache unterscheidet man zwischen speed für den Betrag und velocity für die Vektorform.
Ändert sich die Geschwindigkeit dann findet eine Beschleunigung statt. Diese Bezeichnung gilt auch wenn die Geschwindigkeit sinkt. Da eine Richtungsänderung zur Änderung des Geschwindigkeitsvektors führt, liegt dem ebenfalls eine Beschleunigung zu Grunde, ohne das sich der Betrag der Geschwindigkeit ändern muss.
 bzw.
bzw. 
Des Weiteren lässt sich die Geschwindigkeit als Ableitung der Energie nach dem Impuls definieren:
 bzw.
bzw.  .
.
Einheiten
SI-Einheit der Geschwindigkeit ist Meter pro Sekunde (m/s). Eine weitere gebräuchliche Einheit der Geschwindigkeit ist Kilometer pro Stunde (km/h).
In der Alltagssprache (auch im Duden) wird auch die Bezeichnung „Stundenkilometer“ verwendet, welche im Sinne von „stündlichen Kilometern“ gemeint ist. Da es jedoch in der Physik Konvention ist, dass eine derartige Zusammensetzung für eine Multiplikation der aufgeführten Einheiten steht, würde „Stundenkilometer“ für die Einheit „km×h“ statt „km/h“ stehen. Deshalb sollte der Ausdruck „Stundenkilometer“ vermieden werden. Im Alltag führt der Begriff nicht zu Missverständnissen, da es keine Größe mit der Einheit „km×h“ gibt. In der geschriebenen Sprache sollte man aber insbesondere bei der Abkürzung „km/h“ den Divisionsstrich nicht weglassen.
Als nicht metrische Einheit wird vor allem in den USA und einigen anderen englischsprachigen Ländern Meilen pro Stunde (mph) benutzt. In der See- und Luftfahrt ist außerdem die Einheit Knoten (kn) gebräuchlich; ein Knoten ist eine Seemeile (sm) pro Stunde. Vertikalgeschwindigkeiten in der motorisierten Luftfahrt, aber auch Luftgeschwindigkeiten zur Kühlung werden oft in Fuß pro Minute (LFM von engl. linear feet per minute) angegeben.
Fast nur in der Luftfahrt wird das Mach verwendet, das keine absolute Größe hat, sondern das Verhältnis der Geschwindigkeit zur lokalen Schallgeschwindigkeit angibt. Die Schallgeschwindigkeit ist stark temperaturabhängig aber nicht luftdruckabhängig. Der Grund für die Nutzung dieser Zahl ist, dass aerodynamische Effekte von ihr abhängen. Beim Erreichen der Schallgeschwindigkeit ändert sich das Strömungsverhalten. Propellermaschinen können beispielsweise nicht schneller als der Schall fliegen, sondern nur einen bestimmten Bruchteil der Schallgeschwindigkeit erreichen, gleichgültig, wie groß diese absolut ist.
Umrechnung gebräuchlicher Geschwindigkeitseinheiten:
- 1 kn = 1 sm/h = 0,5144 m/s = 1,852 km/h;
- 1 m/s = 3,6 km/h (exakt) = 1,944 kn = 2,237 mph;
- 1 km/h = 5/18 m/s =
 m/s ≈ 0,2778 m/s = 0,540 kn = 0,6214 mph;
m/s ≈ 0,2778 m/s = 0,540 kn = 0,6214 mph; - 1 mph = 0,8690 kn = 0,44704 m/s (exakt) = 1,609344 km/h (exakt);
- 100 ft/min = 0,508 m/s (exakt);
- c = 299.792.458 m/s (exakt) = 582.749.918 kn = 670.616.629 mph = 1.079.252.848,8 km/h (exakt).
Die Lichtgeschwindigkeit c ist eine wichtige Naturkonstante der Physik. Mit dieser Geschwindigkeit breiten sich elektromagnetische Wellen, also auch das Licht, im Vakuum aus. Außerdem ist die Lichtgeschwindigkeit nach der Relativitätstheorie die höchste (lokal) mögliche Geschwindigkeit für Bewegung und Informationsübertragung.
Grundformen der Bewegung
Sollen der Zusammenhang von komplexen Bewegungen und Geschwindigkeit untersucht werden, hilft zum Verständnis der Abläufe und Begrifflichkeiten die Betrachtung grundlegender Bewegungsformen.
Den Trivialfall bildet ein im Bezugssystem ruhender Punkt, der eine Geschwindigkeit von null besitzt.
Geradlinige Bewegung
Bei der gleichförmigen Bewegung weist der Geschwindigkeitsvektor einen konstanten Wert auf. Das bedeutet weder die Richtung der Bewegung ändert sich noch der Betrag der Geschwindigkeit, weswegen keine Beschleunigung stattfindet.
Bei der gleichmäßig beschleunigten Bewegung nimmt der Betrag der Geschwindigkeit stetig zu. Eine Richtungsänderung findet jedoch nicht statt. Der Beschleunigungsvektor und Geschwindigkeitsvektor liegen folglich auf der selben Linie, können jedoch in die entgegengesetzte Richtung zeigen.
Kreisbewegung
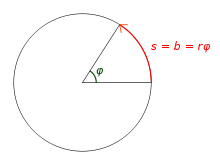
Ein Körper soll sich mit konstanter Winkelgeschwindigkeit auf einer Kreisbahn bewegen, dann ändert sich der Betrag der Geschwindigkeit nicht, jedoch findet eine fortwährende Richtungsänderung statt. Daher muss eine Beschleunigung vorliegen, die jedoch zu jedem Zeitpunkt senkrecht zum Geschwindigkeitsvektor erfolgt und einen konstanten Betrag besitzt, damit die Richtungsänderung eine konstante Rate aufweist. Der Geschwindigkeitsvektor liegt immer tangential zur Kreisbahn und die Beschleunigung zeigt immer radial zum Kreismittelpunkt und trägt die Bezeichnung Zentripetalbeschleunigung.
Ändert sich die Geschwindigkeit mit der sich der Körper im Kreis bewegt erfährt er eine Tangentialbeschleunigung zusätzlich zur Zentripetalbeschleunigung, wobei die Zentripetalbeschleunigung sich jeweils in Relation zur Geschwindigkeit ändert.
Beliebige Bewegung
Die Geschwindigkeit einer beliebigen Bewegungen weist über die Zeit weder einen konstanten Betrag auf noch hat deren Bahn immer die gleiche Richtungsänderung (Krümmungsradius). Doch nun kann die Änderung des Geschwindigkeitvektors in zwei charakteristische Phänomene aufgeteilt werden der Tangental- und der Zentripetalbeschleunigung.
Tangential- und Radialgeschwindigkeit
Die Radialgeschwindigkeit bezeichnet die Komponente eines Geschwindigkeitsvektors längs der Verbindungslinie zwischen dem bewegten Objekt und dem Koordinatenursprung. Senkrecht darauf steht der Vektor für die Tangentialgeschwindigkeit (auch Umfanggeschwindigkeit). Somit ergibt sich:
Das Kreuzprodukt aus Winkelgeschwindigkeit und dem momentanen Ortsvektor liefert die Tangentialgeschwindigkeit.
Aus der Änderung des Abstands zum Koordinatenursprung (Radius) folgt die Radialgeschwindigkeit.
Absolut-, Relativ-, und Führungsgeschwindigkeit
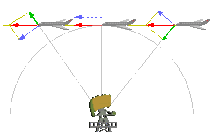
Es sei ein beliebiges Inertialsystem angenommen aus dem heraus ein Körper beobachtet wird. In diesem Bezugssystem bewegt sich der Körper mit Absolutgeschwindigkeit. Nun kommt ein bewegtes Bezugssystem hinzu. Dort besitzt der Körper eine Relativgeschwindigkeit und die Verschiebung des bewegten Bezugssystems trägt die Bezeichnung Führungsgeschwindigkeit.
Zur besser Vorstellung des Sachverhalts ein Beispiel: Beim (näherungsweise) inertialen Beobachter handelt es sich um einen wartenden Passagier im Bahnhof, das bewegte Bezugssystem stellt ein durchfahrender Zug dar und der bewegte Körper sei der Schaffner, der durch den Zug läuft.
- Relativgeschwindigkeit in der Astronomie
Für die Astronomie spielt die absolute Geschwindigkeit keinerlei Rolle, weil prinzipiell kein absolut ruhendes Bezugsystem existiert. Die Koordinatenachsen besitzen eine feste Ausrichtung zum Fixsternhimmel und das Bezugsystem ruht im jeweiligen Baryzentrum. So beträgt etwa die Geschwindigkeit des Mondes:
Geschwindigkeit des Mondes Mittlere Bahngeschwindigkeit
(um den Erde-Mond-Schwerpunkt)um die Sonne/Baryzentrum des Sonnensystems um das galaktische Zentrum in Bezug zur Andromeda Geschwindigkeit in km/s 1,02 ± 5,5 % mensal 29,78 ± 1,51 (± 5,1 % annual) ~ 250
(je galaktischem Jahr, genaue Schwankungen unbekannt)266 ± 31,3 (annual) Anteil der mittleren Bahngeschwindigkeit an der mittleren Relativgeschwindigkeit in Prozent 100 % 3,4 % 0,4 % 0,37 % Für ferne Objekte des Universums ist die Geschwindigkeit primär von der Ausdehnung der Raumzeit bestimmt, und wird etwa als Rotverschiebung gemessen. Daher spielt in der Astronomie ausschließlich die Darstellung der Relativgeschwindigkeit in Bezug zu einem ausgewählten Gravizentrum (Erde-Mond-System, Sonnensystem, Erdorbit eines Satelliten) bzw. zum Beobachtungsort eine Rolle.
Geschwindigkeit zahlreicher Teilchen
Die Geschwindigkeiten in einem strömenden Medium können als Vektorfeld aufgefasst werden.
Siehe auch: StrömungsfeldRelativitätstheorie
Solange die Geschwindigkeit eines beobachteten Objekts einen deutlich kleineren Wert als die Lichtgeschwindigkeit aufweist gelten in guter Näherung die Gesetze der klassischen Mechanik. Genauere Betrachtungen erfordern die Beachtung der speziellen Relativitätstheorie.
Geschwindigkeit, Beschleunigung und Ruck
Die Ableitung des Ortes nach der Zeit ergibt die Geschwindigkeit:

Die zweite Ableitung des Ortes nach der Zeit, also die Ableitung der Geschwindigkeit, ist die Beschleunigung:

Die dritte Ableitung schließlich, also nunmehr die Ableitung der Beschleunigung nach der Zeit, gibt den Ruck an:

Geschichtliche Anmerkung
Galileo Galilei definierte wohl als Erster die Geschwindigkeit gleichförmig-geradliniger Bewegung geometrisch, und zwar als Proportionalität der vom bewegten Körper zurückgelegten Strecken s zu den dazu benötigten Zeiten t.[1] Dies entspricht in heutigen Begriffen der Durchschnittsgeschwindigkeit.
Siehe auch
- Ausbreitungsgeschwindigkeit
- Durchsatz
- Datendurchsatz („Übertragungsgeschwindigkeit“)
- chemische Reaktionsgeschwindigkeit
- Größenordnung (Geschwindigkeit)
- Geschwindigkeit (Straßenverkehr), Reisegeschwindigkeit
- Hodograph
Einzelnachweise
- ↑ Galileo Galilei: Discorsi e dimostrazioni matematiche intorno a due nuove scienze attinenti alla mecanica ed i movimenti locali, Leiden 1638
Weblinks
 Wiktionary: Geschwindigkeit – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Wiktionary: Geschwindigkeit – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen Wikibooks: Formelsammlung Mechanik – Lern- und Lehrmaterialien
Wikibooks: Formelsammlung Mechanik – Lern- und Lehrmaterialien- Versuche und Aufgaben zur Geschwindigkeit
- Geschwindigkeitsumrechner Online und als C-Programm zum Download
Kategorien:- Kinematik
- Physikalische Größenart
Wikimedia Foundation.