- Automorphismus
-
In der Mathematik ist ein Automorphismus (von griechisch αὐτός auto selbst und griechisch μορφή morph Gestalt, Form) eine Abstraktion des Symmetriebegriffs.
Inhaltsverzeichnis
Von Symmetrien zu Automorphismen
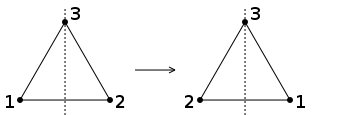
Ein gleichseitiges Dreieck hat drei Symmetrieachsen:
Außerdem verfügt es über eine dreizählige Drehsymmetrie. Um die Symmetrieeigenschaft mathematisch zu fassen, betrachtet man die zugehörigen Symmetrieabbildungen. Zu jeder Symmetrieachse gehört die Spiegelung an der Achse:
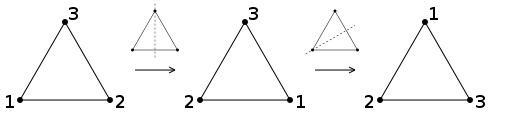
Die Ziffern dienen nur dazu, die Abbildung zu beschreiben, es ist zweimal dasselbe Dreieck. Symmetrieabbildungen können nacheinander ausgeführt werden. Im folgenden Beispiel ist die Hintereinanderausführung zweier Spiegelungen eine Drehung um 120°:
Führt man zweimal dieselbe Spiegelung nacheinander aus, erhält man insgesamt die Abbildung, die nichts verändert, die identische Abbildung. Wenn die Hintereinanderausführung zweier Symmetrieabbildungen wieder eine Symmetrieabbildung sein soll, muss man also die identische Abbildung zulassen. Eine Figur ist unsymmetrisch, wenn sie nur diese eine, triviale Symmetrieabbildung zulässt. Die Gesamtheit der Symmetrieabbildungen bildet eine Gruppe, die Symmetriegruppe.
In der Mathematik betrachtet man häufig Objekte, die aus einer Grundmenge G und einer Zusatzstruktur S bestehen, und in der Regel gibt es eine kanonische Konstruktion, die aus der Zusatzstruktur S auf G und einer Bijektion
 eine Struktur Sf auf H erzeugt. Insbesondere ist das für Bijektionen
eine Struktur Sf auf H erzeugt. Insbesondere ist das für Bijektionen  möglich.
möglich.Auf das Symmetriebeispiel übertragen entspricht G der Ebene und S dem Dreieck. Für eine Kongruenzabbildung
 ist Sf das Bilddreieck. Symmetrieabbildungen zeichnen sich durch S = Sf aus. Im abstrakten Kontext nennt man Bijektionen
ist Sf das Bilddreieck. Symmetrieabbildungen zeichnen sich durch S = Sf aus. Im abstrakten Kontext nennt man Bijektionen  , die S = Sf erfüllen, Automorphismen von (G,S). Diese Definition deckt die meisten Fälle ab, seien es Graphen, topologische Räume oder algebraische Strukturen wie Vektorräume.
, die S = Sf erfüllen, Automorphismen von (G,S). Diese Definition deckt die meisten Fälle ab, seien es Graphen, topologische Räume oder algebraische Strukturen wie Vektorräume.Werden die Zusatzstrukturen komplizierter, kann die harmlos erscheinende Bedingung S = Sf Probleme bereiten: Definiert man differenzierbare Mannigfaltigkeiten als Grundmengen mit Topologie und einem Atlas A, erhält man unter Umständen unter einem Homöomorphismus f einen kompatiblen, aber nicht identischen Atlas Af. Würde man aber in der Definition einen maximalen Atlas fordern, wäre A = Af für ein solches f.
Die Kategorientheorie löst dieses und andere Probleme dadurch, dass sie eine bereits vorhandene Definition für strukturkompatible Abbildungen voraussetzt (Morphismen; es muss sich nicht um tatsächliche Abbildungen handeln). Darauf aufbauend ersetzt sie die Forderung der Bijektivität (die im abstrakten Kontext nicht mehr zur Verfügung steht) durch die Existenz eines inversen Morphismus.
Definition
Algebraische Strukturen
Sei (A,(fi)) eine algebraische Struktur, also eine Menge A zusammen mit einer endlichen Anzahl an Verknüpfungen (fi). Eine solche algebraische Struktur könnte beispielsweise ein Vektorraum
 , eine Gruppe (A, * ) oder ein Ring (A,( + , * )) sein. Dann versteht man in der Algebra unter einem Automorphismus
, eine Gruppe (A, * ) oder ein Ring (A,( + , * )) sein. Dann versteht man in der Algebra unter einem Automorphismus  eine bijektive Abbildung der Menge A auf sich selbst, die linear (beziehungsweise homomorph) ist, das heißt es gilt
eine bijektive Abbildung der Menge A auf sich selbst, die linear (beziehungsweise homomorph) ist, das heißt es giltfür alle
 . Die Umkehrfunktion
. Die Umkehrfunktion  ist unter diesen Umständen automatisch linear.
ist unter diesen Umständen automatisch linear.Kategorientheorie
Sei X ein Objekt. Ein Morphismus
 heißt ein Automorphismus, wenn er ein beidseitiges Inverses
heißt ein Automorphismus, wenn er ein beidseitiges Inverses  besitzt. Das heißt falls ein
besitzt. Das heißt falls ein  existiert, so dass
existiert, so dass und
und 
gilt.
Ein Automorphismus ist damit dasselbe wie
- ein Isomorphismus, dessen Quelle und Ziel gleich sind, und
- ein invertierbarer Endomorphismus.
Für algebraische Strukturen ist die Definition äquivalent zu der im vorherigen Abschnitt.
Automorphismengruppe
- Die Menge aller Automorphismen eines Objekts X bildet mit der Verkettung als Verknüpfung eine Gruppe, die mit Aut(X) bezeichnet wird.
- Ist G eine Gruppe, nennt man einen Homomorphismus
 eine Gruppenoperation von G auf X.
eine Gruppenoperation von G auf X. - Ist
 ein kovarianter Funktor und X ein Objekt von C, so induziert F einen Gruppenhomomorphismus
ein kovarianter Funktor und X ein Objekt von C, so induziert F einen Gruppenhomomorphismus  . (Für kontravariante Funktoren muss man noch mit der Inversion
. (Für kontravariante Funktoren muss man noch mit der Inversion  verketten.) Ist eine Gruppenoperation von G auf X gegeben, so erhält man auf diesem Wege eine Operation von G auf F(X).
verketten.) Ist eine Gruppenoperation von G auf X gegeben, so erhält man auf diesem Wege eine Operation von G auf F(X).
Spezielle Strukturen
Graphen
Allgemeines
Ein Automorphismus eines Graphen G = (V,E) mit Knotenmenge V und Kantenmenge E ist eine bijektive Abbildung
 , so dass
, so dass  für alle
für alle  gilt.
gilt.Ein Automorphismus eine Graphen induziert einen Automorphismus des Komplementgraphen.
Der Satz von Frucht besagt, dass zu jeder Gruppe Γ ein Graph G existiert, so dass Aut(G) isomorph zu Γ ist.
Beispiel
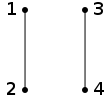
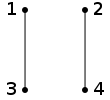
Sei V = {1,2,3,4} und E = {{1,2},{3,4}}:
Automorphismen von G = (V,E) sind Permutationen von V, so dass die Anwendung der Permutation auf das Diagramm wieder eine Veranschaulichung desselben Graphen ergibt. Beispiel: Die Permutation
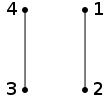
 ist ein Automorphismus, weil die Kanten nach wie vor zwischen 1 und 2 sowie zwischen 3 und 4 verlaufen:
ist ein Automorphismus, weil die Kanten nach wie vor zwischen 1 und 2 sowie zwischen 3 und 4 verlaufen:Die Permutation
 ist kein Automorphismus, weil die Kanten im neuen Bild {1,3} und {2,4} sind:
ist kein Automorphismus, weil die Kanten im neuen Bild {1,3} und {2,4} sind:Die Automorphismengruppe des Graphen ist isomorph zur Diedergruppe der Ordnung 8, sein Komplement ist ein 4-Zyklus.
Vektorräume
Ein Automorphismus eines Vektorraums V ist eine bijektive lineare Abbildung
 .
.Für endlichdimensionale Vektorräume V sind Automorphismen genau diejenigen lineare Abbildungen
 , deren Abbildungsmatrix bezüglich einer beliebigen Basis regulär ist. Die Automorphismengruppe wird häufig als GL(V) notiert.
, deren Abbildungsmatrix bezüglich einer beliebigen Basis regulär ist. Die Automorphismengruppe wird häufig als GL(V) notiert.Gruppen
Allgemeines
Ein Automorphismus einer Gruppe G ist ein bijektiver Gruppenhomomorphismus, das heißt eine bijektive Abbildung
 mit ϕ(gh) = ϕ(g)ϕ(h) für alle
mit ϕ(gh) = ϕ(g)ϕ(h) für alle  .
.Automorphismen erhalten alle Eigenschaften und Konstruktionen, die mit Hilfe des Gruppengesetzes charakterisiert werden können. Beispiele: Jeder Automorphismus induziert einen Automorphismus des Zentrums, erhält die Ordnung von Elementen (d.h. o(ϕ(g)) = o(g)) und bildet Erzeugendensysteme auf Erzeugendensysteme ab.
Innere Automorphismen
Ist G eine Gruppe und
 fest, dann ist
fest, dann ist  , ih(g) = hgh − 1 ein Automorphismus von G, genannt Konjugation mit h. Automorphismen, die auf diesem Weg entstehen, heißen innere Automorphismen. Weil
, ih(g) = hgh − 1 ein Automorphismus von G, genannt Konjugation mit h. Automorphismen, die auf diesem Weg entstehen, heißen innere Automorphismen. Weil  ein Homomorphismus
ein Homomorphismus  ist und ih genau dann der triviale Automorphismus ist, wenn h im Zentrum von G liegt, ist die Menge Inn(G) aller inneren Automorphismen eine zu G / Z(G) isomorphe Untergruppe von Aut(G). Sie ist sogar ein Normalteiler in Aut(G), und die Faktorgruppe wird mit Out(G) bezeichnet. Die Einschränkung auf das Zentrum liefert einen Homomorphismus
ist und ih genau dann der triviale Automorphismus ist, wenn h im Zentrum von G liegt, ist die Menge Inn(G) aller inneren Automorphismen eine zu G / Z(G) isomorphe Untergruppe von Aut(G). Sie ist sogar ein Normalteiler in Aut(G), und die Faktorgruppe wird mit Out(G) bezeichnet. Die Einschränkung auf das Zentrum liefert einen Homomorphismus  .
.Für abelsche Gruppen sind alle inneren Homomorphismen trivial, und Aut(G) = Out(G).
Für eine Untergruppe
 erhält man durch Einschränkung der inneren Automorphismen einen injektiven Homomorphismus
erhält man durch Einschränkung der inneren Automorphismen einen injektiven Homomorphismus  . Siehe Normalisator und Zentralisator.
. Siehe Normalisator und Zentralisator.Beispiele
- Die bijektive Abbildung
 ,
,  , ist genau dann ein Homomorphismus und damit ein Automorphismus, wenn G abelsch ist.
, ist genau dann ein Homomorphismus und damit ein Automorphismus, wenn G abelsch ist. - Die Gruppe
 hat genau einen nichttrivialen Automorphismus, nämlich
hat genau einen nichttrivialen Automorphismus, nämlich  . Das folgt daraus, dass ein Automorphismus ein Erzeugendensystem auf ein Erzeugendensystem abbildet.
. Das folgt daraus, dass ein Automorphismus ein Erzeugendensystem auf ein Erzeugendensystem abbildet. - Die Automorphismengruppe der kleinschen Vierergruppe ist isomorph zur symmetrischen Gruppe S3.
- Die Automorphismengruppe der Gruppe
 ist
ist  (durch Multiplikation), die Automorphismengruppe der Gruppe
(durch Multiplikation), die Automorphismengruppe der Gruppe  ist überabzählbar.
ist überabzählbar. - Der Automorphismus
 von
von  ist kein innerer Automorphismus, weil seine Einschränkung auf das Zentrum, die Untergruppe der Skalarmatrizen, nicht trivial ist.
ist kein innerer Automorphismus, weil seine Einschränkung auf das Zentrum, die Untergruppe der Skalarmatrizen, nicht trivial ist.
Verwandte Themen
- Untergruppen, die invariant unter allen Automorphismen sind, heißen charakteristische Untergruppen.
Körper
Ein Automorphismus eines Körpers K ist eine bijektive Abbildung
 , die ϕ(x + y) = ϕ(x) + ϕ(y) und ϕ(xy) = ϕ(x)ϕ(y) für alle
, die ϕ(x + y) = ϕ(x) + ϕ(y) und ϕ(xy) = ϕ(x)ϕ(y) für alle  erfüllt. Ist L / K eine Körpererweiterung, dann nennt man diejenigen Automorphismen ϕ von L, die ϕ(x) = x für alle
erfüllt. Ist L / K eine Körpererweiterung, dann nennt man diejenigen Automorphismen ϕ von L, die ϕ(x) = x für alle  erfüllen, die K-Automorphismen von L. Sie bilden eine Gruppe, notiert AutK(L) oder Aut(L / K). Ein Automorphismus von L ist genau dann ein K-Automorphismus, wenn er eine K-lineare Abbildung ist.
erfüllen, die K-Automorphismen von L. Sie bilden eine Gruppe, notiert AutK(L) oder Aut(L / K). Ein Automorphismus von L ist genau dann ein K-Automorphismus, wenn er eine K-lineare Abbildung ist.- Die Konjugation
 für
für  ist ein
ist ein  -Automorphismus des Körpers
-Automorphismus des Körpers  der komplexen Zahlen.
der komplexen Zahlen. - Der Körper der reellen Zahlen besitzt keine nichttrivialen Automorphismen.
- Ist K ein endlicher oder allgemeiner perfekter Körper der Charakteristik p > 0, dann ist
 ein Automorphismus von K, der Frobeniusautomorphismus.
ein Automorphismus von K, der Frobeniusautomorphismus. - Ist L ein Körper und
 eine endliche Untergruppe, dann ist
eine endliche Untergruppe, dann ist  ein Unterkörper von K mit [L:K] = | G | , und L / K ist eine Galoiserweiterung. Die Galoistheorie stellt weitere Verbindungen zwischen Körpererweiterungen und Automorphismengruppen her.
ein Unterkörper von K mit [L:K] = | G | , und L / K ist eine Galoiserweiterung. Die Galoistheorie stellt weitere Verbindungen zwischen Körpererweiterungen und Automorphismengruppen her.
Algebren
Für Algebren kann man wie bei Gruppen innere Automorphismen als Konjugation mit einer Einheit definieren. Innere Automorphismen sind trivial auf dem Zentrum, und der Satz von Skolem-Noether besagt, dass für eine halbeinfache Algebra auch die Umkehrung gilt.
Funktionentheorie
In der Funktionentheorie sind die Morphismen die holomorphen Funktionen und die Automorphismen die konformen Selbstabbildungen. Die Automorphismengruppe bspw. der offenen Einheitskreisscheibe
 ist gegeben durch:
ist gegeben durch:Literatur
- Serge Lang, Algebra. Springer-Verlag 2002
Wikimedia Foundation.