- Sekans und Kosekans
-
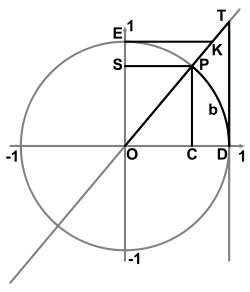
Sekans und Kosekans sind trigonometrische Funktionen. Der Sekans wird mit sec(x) bezeichnet, der Kosekans mit csc(x). Die Funktionen haben ihren Namen durch die Definition im Einheitskreis. Die Funktionswerte entsprechen der Länge von Sekantenabschnitten:
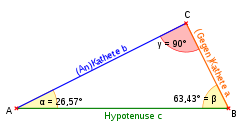
Im rechtwinkligen Dreieck ist der Sekans das Verhältnis der Hypotenuse zur Ankathete und damit die Kehrwertfunktion der Kosinusfunktion.
Der Kosekans ist das Verhältnis der Hypotenuse zur Gegenkathete und damit die Kehrwertfunktion der Sinusfunktion:
Inhaltsverzeichnis
Eigenschaften
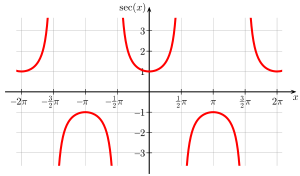
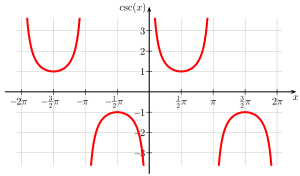
Graphen
Definitionsbereich
-
Sekans: 
Kosekans: 
Wertebereich
Periodizität
- Periodenlänge

Symmetrien
-
Sekans: Achsensymmetrie: f(x) = f( − x) Kosekans: Punktsymmetrie: f( − x) = − f(x)
Polstellen
-
Sekans: 
Kosekans: 
Extremwerte
-
Sekans: Minima: 
Maxima: 
Kosekans: Minima: 
Maxima: 
Weder die Sekansfunktion noch die Kosekansfunktion haben horizontale Asymptoten, Sprungstellen, Wendepunkte oder Nullstellen.
Umkehrfunktionen
Sekans:
- Auf einer halben Periodenlänge, z. B.
![x \in [0 , \pi]](0/ed0d5fb967bb60be6166d88803441d2f.png) ist die Funktion umkehrbar (Arkussekans):
ist die Funktion umkehrbar (Arkussekans): 
Kosekans
- Auf einer halben Periodenlänge, z. B.
![x \in \left[-\frac{\pi}{2} , \frac{\pi}{2} \right]](a/48af4ce3aea5ab5bbfdca2a3cb0786e2.png) ist die Funktion umkehrbar (Arkuskosekans):
ist die Funktion umkehrbar (Arkuskosekans): 
Reihenentwicklung
Sekans:
Kosekans:
Ableitung
Sekans:
Kosekans
Integral
Sekans:
Kosekans
Komplexes Argument
 mit
mit 
 mit
mit 
Siehe auch
Weblinks
Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Sekans Hyperbolicus und Kosekans Hyperbolicus — Sekans Hyperbolicus (blau) und Kosekans Hyperbolicus (rot) Die Funktionen Kosekans Hyperbolicus (csch) und Sekans Hyperbolicus (sech) sind Hyperbelfunktionen. Sie ergeben sich als Kehrwert von Sinus Hyperbolicus bzw. Kosinus Hyperbolicus.… … Deutsch Wikipedia
Kosekans Hyperbolicus — Sekans Hyperbolicus (blau) und Kosekans Hyperbolicus (rot) Die Funktionen Sekans Hyperbolicus ( ) und Kosekans Hyperbolicus ( ) sind Hyperbelfunktionen. Inhaltsverzeichnis 1 Definitionen 2 … Deutsch Wikipedia
Sekans Hyperbolicus — (blau) und Kosekans Hyperbolicus (rot) Die Funktionen Sekans Hyperbolicus ( ) und Kosekans Hyperbolicus ( ) sind Hyperbelfunktionen. Inhaltsverzeichnis 1 Definitionen 2 … Deutsch Wikipedia
Kosekans — Definitionen am Einheitskreis Sekans und Kosekans sind trigonometrische Funktionen. Der Sekans wird mit sec(x) bezeichnet, der Kosekans mit csc(x). Die Funktionen haben ihren Namen durch die Definition im Einheitskreis. Die Funktionswerte… … Deutsch Wikipedia
Sekans — Definitionen am Einheitskreis Sekans und Kosekans sind trigonometrische Funktionen. Der Sekans wird mit sec(x) bezeichnet, der Kosekans mit csc(x). Die Funktionen haben ihren Namen durch die Definition im Einheitskreis. Die Funktionswerte… … Deutsch Wikipedia
Area-Kosekans Hyperbolicus — Areasekans Hyperbolicus und Areakosekans Hyperbolicus gehören zu den Areafunktionen. Sie sind die Umkehrfunktionen zu Sekans Hyperbolicus bzw. Kosekans Hyperbolicus. Als Funktionen werden sie oder seltener bzw. und seltener ges … Deutsch Wikipedia
Arkus-Kosekans — Arkussekans und Arkuskosekans sind trigonometrische Funktionen. Sie sind die Umkehrfunktionen der Sekansfunktion bzw. der Kosekansfunktion und damit Arkusfunktionen. Da die Sekans und die Kosekansfunktion periodisch sind, wird zur Umkehrung der… … Deutsch Wikipedia
Arkus Kosekans — Arkussekans und Arkuskosekans sind trigonometrische Funktionen. Sie sind die Umkehrfunktionen der Sekansfunktion bzw. der Kosekansfunktion und damit Arkusfunktionen. Da die Sekans und die Kosekansfunktion periodisch sind, wird zur Umkehrung der… … Deutsch Wikipedia
Arkus-Sekans — Arkussekans und Arkuskosekans sind trigonometrische Funktionen. Sie sind die Umkehrfunktionen der Sekansfunktion bzw. der Kosekansfunktion und damit Arkusfunktionen. Da die Sekans und die Kosekansfunktion periodisch sind, wird zur Umkehrung der… … Deutsch Wikipedia
Arkus Sekans — Arkussekans und Arkuskosekans sind trigonometrische Funktionen. Sie sind die Umkehrfunktionen der Sekansfunktion bzw. der Kosekansfunktion und damit Arkusfunktionen. Da die Sekans und die Kosekansfunktion periodisch sind, wird zur Umkehrung der… … Deutsch Wikipedia