- Tangens und Kotangens
-
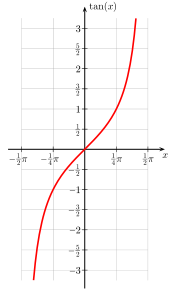
 Schaubild Tangens (im Bogenmaß)
Schaubild Tangens (im Bogenmaß)
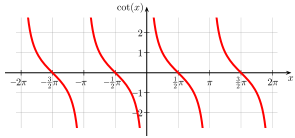 Schaubild Kotangens (im Bogenmaß)
Schaubild Kotangens (im Bogenmaß)
Tangens und Kotangens sind trigonometrische Funktionen und spielen in der Mathematik und ihren Anwendungsgebieten eine herausragende Rolle. Der Tangens des Winkels x wird mit
 bezeichnet, der Kotangens des Winkels x mit
bezeichnet, der Kotangens des Winkels x mit  .
.Definition
Historisch/geometrisch
Die Bezeichnung „Tangens“ stammt von dem in Flensburg geborenen Mathematiker Thomas Finck (1561–1656), der sie 1583 einführte. Die Bezeichnung "Kotangens" entwickelte sich aus complementi tangens, also Tangens des Komplementärwinkels.[1]
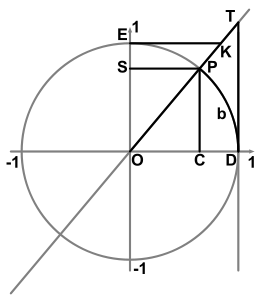
Die Wahl des Namens Tangens erklärt sich unmittelbar durch die Definition im Einheitskreis. Die Funktionswerte entsprechen der Länge eines Tangentenabschnitts:
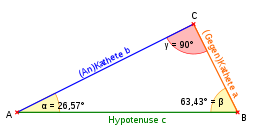
In einem rechtwinkligen Dreieck ist der Tangens eines Winkels α das Längenverhältnis von Gegenkathete zu Ankathete und der Kotangens das Längenverhältnis von Ankathete zu Gegenkathete:
Daraus folgt unmittelbar:
sowie
Formal – mit Definitions- und Wertebereich
Formal kann die Tangensfunktion mittels der Sinus- und Kosinusfunktionen durch
 mit
mit 
definiert werden,[2] wobei der Wertebereich W je nach Anwendung die reellen
 oder die komplexen Zahlen
oder die komplexen Zahlen  sind. Um zu verhindern, dass der Nenner cosx Null wird, werden beim Definitionsbereich D die Nullstellen der Cosinus-Funktion weggelassen:
sind. Um zu verhindern, dass der Nenner cosx Null wird, werden beim Definitionsbereich D die Nullstellen der Cosinus-Funktion weggelassen:im Reellen bzw.
im Komplexen.
Der Kotangens kann analog dazu durch
 mit
mit 
definiert werden, wobei sich für dessen Definitionsbereich
im Reellen bzw.
im Komplexen ergibt, wenn gewährleistet werden soll, dass der Nenner sin x ungleich Null ist.
Für den gemeinsamen Definitionsbereich von tan und cot
gilt
Eigenschaften
Periodizität
- Periodenlänge π :

Monotonie
Tangens: Im jeweiligen Intervall streng monoton steigend.
Kotangens: Im jeweiligen Intervall streng monoton fallend.
Symmetrien
Punktsymmetrisch zum Koordinatenursprung:
Nullstellen
-
Tangens: 
Kotangens: 
Polstellen
-
Tangens: 
Kotangens: 
Wendestellen
-
Tangens: 
Kotangens: 
Sowohl die Tangensfunktion als auch die Kotangensfunktion haben Asymptoten, aber keine Sprungstellen oder Extrema.
Wichtige Funktionswerte
Tangens Kotangens Ausdruck num. Wert 


0 


0,4142135... 


0,5773502... 


1 


1,7320508... 


2,4142135... 


Polstelle Umkehrfunktion
Durch passende Einschränkung der Definitionsbereiche erhält man eine Bijektion
- Tangens
 .
.
Ihre Umkehrfunktion
heißt Arkustangens und ist folglich ebenfalls bijektiv.
- Kotangens
 .
.
Ihre Umkehrfunktion
heißt Arkuskotangens und ist folglich ebenfalls bijektiv.
Reihenentwicklung
 Tangens für |x| < ½π (im Bogenmaß)
Tangens für |x| < ½π (im Bogenmaß)
- Tangens
- Die Taylorreihe mit dem Entwicklungspunkt x = 0 (MacLaurinsche Reihe) lautet für
 [3]
[3] 
Dabei sind mit Bn die Bernoulli-Zahlen bezeichnet.
- Kotangens
- Die Laurent-Reihe lautet für 0 < | x | < π[4]

Die Partialbruchzerlegung des Kotangens lautet für

Ableitung
Bei der Ableitung von Tangens und Kotangens tauchen die ansonsten eher wenig gebräuchlichen trigonometrischen Funktionen Sekans und Kosekans auf:
Die n-ten Ableitungen lassen sich mit der Polygammafunktion ausdrücken:
Integral
- Tangens
 mit
mit 

- Kotangens
 mit
mit 

Komplexes Argument
 mit
mit 
 mit
mit 
Additionstheoreme
Die Additionstheoreme für Tangens und Kotangens lauten
Eine symmetrische Formulierung lautet: Genau dann gilt
 bzw.
bzw. 
wenn x + y + z ein Vielfaches von π ist.
Rationale Parametrisierung
Der Tangens des halben Winkels kann dazu verwendet werden, verschiedene trigonometrische Funktionen durch rationale Ausdrücke zu beschreiben: Ist
 , so ist
, so istInsbesondere ist
eine Parametrisierung des Einheitskreises mit Ausnahme des Punktes ( − 1,0) (der dem Parameter
 entspricht). Einem Parameterwert t entspricht dabei der zweite Schnittpunkt der Verbindungsgeraden von ( − 1,0) und (1,2t) mit dem Einheitskreis.
entspricht). Einem Parameterwert t entspricht dabei der zweite Schnittpunkt der Verbindungsgeraden von ( − 1,0) und (1,2t) mit dem Einheitskreis.Anwendung: Tangens und Steigungswinkel
Der Tangens liefert eine wichtige Kennzahl für lineare Funktionen: Jede lineare Funktion
 besitzt als Graphen eine Gerade. Der Tangens des Winkels zwischen der Geraden und der x-Achse entspricht genau der Steigung m der Geraden, d. h.
besitzt als Graphen eine Gerade. Der Tangens des Winkels zwischen der Geraden und der x-Achse entspricht genau der Steigung m der Geraden, d. h. 
Bei negativer Steigung (m < 0) gilt: m = − tan α
Die als Steigung einer Straße angegebene Prozentzahl ist der Tangens des Steigungswinkels.
Anwendung in der Physik
Tangens und Kotangens können benutzt werden, um die zeitliche Abhängigkeit der Geschwindigkeit beim Wurf eines Körpers nach oben zu beschreiben, wenn für den Strömungswiderstand der Luft eine turbulente Strömung angesetzt wird (Newton-Reibung). Das Koordinatensystem werde so gelegt, dass die Ortsachse nach oben zeigt. Für die Geschwindigkeit gilt dann eine Differenzialgleichung der Form
 mit der Schwerebeschleunigung g und einer Konstanten k > 0. Dann ergibt sich:
mit der Schwerebeschleunigung g und einer Konstanten k > 0. Dann ergibt sich: mit
mit  ,
,
wobei
 die Grenzgeschwindigkeit ist, die beim Fall mit Luftwiderstand erreicht wird. Wegen der oben angegebenen engen Zusammenhänge zwischen Kotangens und Tangens kann man diese zeitliche Abhängigkeit auch genauso gut mit Hilfe des Tangens ausdrücken:
die Grenzgeschwindigkeit ist, die beim Fall mit Luftwiderstand erreicht wird. Wegen der oben angegebenen engen Zusammenhänge zwischen Kotangens und Tangens kann man diese zeitliche Abhängigkeit auch genauso gut mit Hilfe des Tangens ausdrücken: mit
mit  .
.
Diese Lösung gilt, bis der Körper den höchsten Punkt seiner Bahn erreicht hat (also wenn v = 0 ist, das heißt für
 ), daran anschließend muss man den Tangens Hyperbolicus verwenden, um den folgenden Fall mit Luftwiderstand zu beschreiben.
), daran anschließend muss man den Tangens Hyperbolicus verwenden, um den folgenden Fall mit Luftwiderstand zu beschreiben.Differentialgleichung
Der Tangens ist eine Lösung der Riccati-Gleichung
- w' = 1 + w2.
Faktorisiert man die rechte Seite, so erhält man
- w' = 1 + w2 = (w + i)(w − i)
mit der imaginären Einheit i. Der Tangens (als komplexe Funktion) hat die Ausnahmewerte i, − i: Diese Werte werden niemals angenommen, da die konstanten Funktionen i und − i Lösungen der Differentialgleichung sind und der Existenz- und Eindeutigkeitssatz ausschließt, dass zwei verschiedene Lösungen an derselben Stelle denselben Wert besitzen.
Siehe auch
Weblinks
 Wiktionary: tan – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Wiktionary: tan – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen Wikiversity: Tangens und Kotangens – Kursmaterialien, Forschungsprojekte und wissenschaftlicher Austausch
Wikiversity: Tangens und Kotangens – Kursmaterialien, Forschungsprojekte und wissenschaftlicher AustauschEinzelnachweise
- ↑ Josef Laub (Hrsg.) Lehrbuch der Mathematik für die Oberstufe der allgemeinbildenden höheren Schulen. 2. Band.. Hölder-Pichler-Tempsky, 2. Auflage, Wien 1977. ISBN 3-209-00159-6, S. 223.
- ↑ Per Dreisatz ist sin/cos = tan/1.
- ↑ Milton Abramowitz and Irene Stegun: Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4 4.3.67
- ↑ Milton Abramowitz and Irene Stegun: Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4 4.3.70
Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Tangens Hyperbolicus und Kotangens Hyperbolicus — Graph des Tangens Hyperbolicus Graph des Kotangens Hyperbol … Deutsch Wikipedia
Kotangens Hyperbolicus — Tangens Hyperbolicus und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens. Inhaltsverzeichnis 1 Schreibweisen 2 Definitionen 3… … Deutsch Wikipedia
Kotangens Hyperbolikus — Tangens Hyperbolicus und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens. Inhaltsverzeichnis 1 Schreibweisen 2 Definitionen 3… … Deutsch Wikipedia
Kotangens hyperbolicus — Tangens Hyperbolicus und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens. Inhaltsverzeichnis 1 Schreibweisen 2 Definitionen 3… … Deutsch Wikipedia
Kotangens hyperbolikus — Tangens Hyperbolicus und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens. Inhaltsverzeichnis 1 Schreibweisen 2 Definitionen 3… … Deutsch Wikipedia
Tangens-Hyperbolicus — und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens. Inhaltsverzeichnis 1 Schreibweisen 2 Definitionen 3 Eigenschaften … Deutsch Wikipedia
Tangens Hyperbolicus — und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens. Inhaltsverzeichnis 1 Schreibweisen 2 Definitionen 3 Eigenschaften … Deutsch Wikipedia
Tangens Hyperbolikus — Tangens Hyperbolicus und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens. Inhaltsverzeichnis 1 Schreibweisen 2 Definitionen 3… … Deutsch Wikipedia
Tangens hyperbolicus — und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens. Inhaltsverzeichnis 1 Schreibweisen 2 Definitionen 3 Eigenschaften … Deutsch Wikipedia
Tangens hyperbolikus — Tangens Hyperbolicus und Kotangens Hyperbolicus sind Hyperbelfunktionen. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens bzw. Hyperbelkotangens oder hyperbolischen Kotangens. Inhaltsverzeichnis 1 Schreibweisen 2 Definitionen 3… … Deutsch Wikipedia