- Arkustangens und Arkuskotangens
-
Der Arkustangens – geschrieben arctan, atan, neuerdings auch tan − 1[1]) – sowie Arkuskotangens – geschrieben arccot, acot, neuerdings auch cot − 1[2] – sind die Umkehrfunktionen der eingeschränkten Tangens- und Kotangensfunktion: Da Tangens und Kotangens periodische Funktionen sind, muss dabei zu ihrer Umkehrung der ursprüngliche Definitionsbereich des Tangens auf das Intervall
![\left]-\pi/2; \pi/2\right[](4/f5476085e738ed8e048b7d0689090318.png) sowie der des Kotangens auf das Intervall ]0;π[ beschränkt werden.
sowie der des Kotangens auf das Intervall ]0;π[ beschränkt werden.Zusammen mit Arkussinus und Arkuskosinus als Umkehrfunktionen des Sinus und Kosinus bildet der Arkustangens den Kern der Klasse der Arkusfunktionen. Aufgrund der heute für Umkehrfunktionen gebräuchlichen allgemeinen Schreibweise f − 1 beginnt dabei aber auch in diesem Fall die namentlich auf Taschenrechnern verbreitete Schreibweise tan − 1 die klassische Schreibweise arctan zu verdrängen, was leicht zu Verwechslungen mit dem Kehrwert des Tangens, dem Kotangens, führen kann.
Inhaltsverzeichnis
Eigenschaften
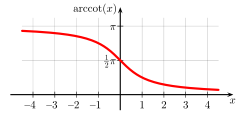
Arkustangens Arkuskotangens Definitionsbereich 

Wertebereich 
0 < f(x) < π Monotonie streng monoton steigend streng monoton fallend Symmetrien Ungerade Funktion:
arctan( − x) = − arctan xPunktsymmetrie zu 
arccot x = π − arccot( − x)Asymptoten  für
für 
 für
für 
 für
für 
Nullstellen x = 0 keine Sprungstellen keine keine Polstellen keine keine Extrema keine keine Wendepunkte (0;0) 
Spezielle Werte
x 








arctan(x) 








Wegen der Punktsymmetrie gelten die entsprechenden Wertepaare auch im Negativen. Solche speziellen Werte gibt es unendlich viele, aufgelistet sind nur die einfachsten.
Reihenentwicklung
Die Taylorreihe des Arkustangens mit dem Entwicklungspunkt x=0 lautet:
Die Taylorreihe des Arkuskotangens mit dem Entwicklungspunkt x=0 lautet:
Diese Reihen konvergieren genau dann, wenn
 und
und  ist. Zur Berechnung des Arkustangens für
ist. Zur Berechnung des Arkustangens für  kann man ihn auf einen Arkustangens von kleineren Argumenten zurückführen. Dazu kann man entweder die Funktionalgleichung hernehmen, oder (um ohne π auszukommen) die Gleichung
kann man ihn auf einen Arkustangens von kleineren Argumenten zurückführen. Dazu kann man entweder die Funktionalgleichung hernehmen, oder (um ohne π auszukommen) die GleichungHiermit lässt sich das Argument nach mehrfacher Anwendung beliebig verkleinern, was eine sehr effiziente Berechnung durch die Reihe ermöglicht.
Berechnung der Kreiszahl
 mit Hilfe des Arkustangens
mit Hilfe des ArkustangensDie Reihenentwicklung kann zur näherungsweisen Berechnung der Zahl π verwendet werden: Die einfachste Formel ist der Spezialfall x = 1, die Leibniz-Formel
Da sie nur sehr langsam konvergiert, verwendete John Machin 1706 die kompliziertere Formel
um die ersten 100 Nachkommastellen von π mit Hilfe der Taylorreihe für den Arkustangens zu berechnen. Letztere konvergiert schneller und wird auch heute noch für die Berechnung von π verwendet.
Funktionalgleichung
Die Arkustangenswerte über 1 oder unter −1 lassen sich aus den Werten zwischen −1 und 1 ableiten:
Die Arkuskotangenswerte über 1 oder unter −1 lassen sich aus den Werten zwischen −1 und 1 ableiten:
Ableitungen
Arkustangens:
Arkuskotangens:
 .
.
Stammfunktionen
Arkustangens:
Der Arkustangens spielt eine wesentliche Rolle bei der symbolischen Integration von Ausdrücken der Form
Ist die Diskriminante D = b2 − 4ac nicht negativ, so kann man eine Stammfunktion mittels Partialbruchzerlegung bestimmen. Ist die Diskriminante negativ, so kann man den Ausdruck durch die Substitution
in die Form
bringen; eine Stammfunktion ist also
Eine Stammfunktion des Arkustangens selbst ist
Arkuskotangens:
Komplexes Argument

 mit
mit 
Anmerkungen
Arkustangens:
Man kann den Arkustangens durch den komplexen Logarithmus ausdrücken:
für z in der 2-fach geschlitzten Ebene:

Arkuskotangens:
Man kann den Arkuskotangens durch einen komplexen Logarithmus ausdrücken:
Zwischen Arkustangens und Arkuskotangens besteht folgende Beziehung:
Näherungsweise Berechnung
Es gelten folgende Näherungen:
Arkustangens, maximale Abweichung unter 0,005 Radianten[3]:
Eine weitere Berechnungsmöglichkeit bietet CORDIC.
Arkuskotangens:
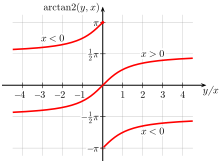
Der „Arkustangens“ mit zwei Argumenten (atan2)
Diese Funktion dient bei der Umrechnung von kartesischen Koordinaten P(x;y) in Polarkoordinaten P(r;φ) der Ermittlung des Winkels φ. Da der einfache Arkustangens nicht die Möglichkeit bietet, den Winkel im korrekten Quadranten zu ermitteln, und außerdem die Tangensfunktion für einen Funktionswert von
 nicht umkehrbar ist, gibt es in vielen Programmiersprachen eine Funktion, die mit 2 Argumenten aufgerufen wird. Sie wird üblicherweise mit
nicht umkehrbar ist, gibt es in vielen Programmiersprachen eine Funktion, die mit 2 Argumenten aufgerufen wird. Sie wird üblicherweise mit  bezeichnet.
bezeichnet.Die Funktion
 kann über die folgende Eigenschaft definiert werden: Sind x,y reelle Zahlen und
kann über die folgende Eigenschaft definiert werden: Sind x,y reelle Zahlen und  , so gilt:
, so gilt: sind hierbei die Polarkoordinaten des Punktes mit den kartesischen Koordinaten (x,y).
sind hierbei die Polarkoordinaten des Punktes mit den kartesischen Koordinaten (x,y).Definition
Eine von mehreren in der Praxis vorkommenden Definitionen:
Für x = y = 0 ist die Funktion manchmal nicht definiert. Auch Sonderfälle wie Not a Number und Inf werden unterschiedlich behandelt.
Wertebereich
Bei der o. g. Definition:
Anmerkungen
Eine weitere Möglichkeit besteht darin, die Funktion
 für (x,y) ≠ (0,0) über den Hauptwert des komplexen Logarithmus zu definieren:
für (x,y) ≠ (0,0) über den Hauptwert des komplexen Logarithmus zu definieren:Diese Funktion wird zum Beispiel in der inversen Kinematik genutzt, um korrekte Gelenkeinstellungen berechnen zu können.
Einzelnachweise
- ↑ Weisstein, Eric W. "Inverse Tangent." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseTangent.html
- ↑ Weisstein, Eric W. "Inverse Cotangent." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseCotangent.html
- ↑ Weitere Approximationen (en)
Siehe auch
Weblinks
 Commons: Arkustangens und Arkuskotangens – Sammlung von Bildern, Videos und Audiodateien
Commons: Arkustangens und Arkuskotangens – Sammlung von Bildern, Videos und AudiodateienPrimäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Arkuskotangens — Arkustangens und Arkuskotangens sind mathematische Funktionen. Sie sind die Umkehrfunktionen des Tangens bzw. des Kotangens und damit Arkusfunktionen. Da der Tangens periodisch ist, wird zur Umkehrung der Definitionsbereich von Tangens auf ( − π… … Deutsch Wikipedia
Arkustangens — und Arkuskotangens sind mathematische Funktionen. Sie sind die Umkehrfunktionen des Tangens bzw. des Kotangens und damit Arkusfunktionen. Da der Tangens periodisch ist, wird zur Umkehrung der Definitionsbereich von Tangens auf ( − π / 2,π / 2)… … Deutsch Wikipedia
Arkussinus und Arkuskosinus — Der Arkussinus geschrieben arcsin, asin, und Arkuskosinus geschrieben arccos, acos,sind die Umkehrfunktionen der eingeschränkten Sinus und Kosinusfunktion: Da Sinus und Kosinus periodische Funktionen sind, muss dabei zu ihrer Umkehrung der… … Deutsch Wikipedia
Kosinus und Sinus — Graphen der Sinus und der Cosinusfunktion Die Sinusfunktion und die Kosinusfunktion (auch Cosinusfunktion) sind elementare mathematische Funktionen aus der Klasse der trigonometrischen Funktionen. Sinus und Kosinus sind grundlegend in allen… … Deutsch Wikipedia
Tangens und Kotangens — Schaubild Tangens (im Bogenmaß) Schaubild Kotangens (im … Deutsch Wikipedia
Sinus und Kosinus — Graphen der Sinusfunktion (rot) und der Kosinusfunktion (blau). Beide Funktionen sind 2π periodisch und nehmen Werte von −1 bis 1 an. Sinus und Kosinusfunktion (auch Cosinusfunktion) sind elementare mathematische Funktionen. Vor Tangens und… … Deutsch Wikipedia
Areasekans Hyperbolicus und Areakosekans Hyperbolicus — gehören zu den Areafunktionen. Sie sind die Umkehrfunktionen zu Sekans Hyperbolicus bzw. Kosekans Hyperbolicus. Als Funktionen werden sie oder seltener bzw. und seltener geschrieben … Deutsch Wikipedia
Areasinus Hyperbolicus und Areakosinus Hyperbolicus — Areasinus Hyperbolicus (abgekürzt , , ; seltener auch ) und Areakosinus Hyperbolicus (abgekürzt , , ; seltener auch … Deutsch Wikipedia
Areatangens Hyperbolicus und Areakotangens Hyperbolicus — sind die Umkehrfunktionen von Tangens Hyperbolicus und Kotangens Hyperbolicus und damit Area Funktionen. Schreibweisen: Letztere wird seltener benutzt, um die Verwechselung mit dem Kehrwert des hyperbolischen (Ko)Tangens zu vermeiden. Es ist … Deutsch Wikipedia
Arkussekans und Arkuskosekans — sind zyklometrische Funktionen. Sie sind die Umkehrfunktionen der Sekansfunktion bzw. der Kosekansfunktion und damit Arkusfunktionen. Da die Sekans und die Kosekansfunktion periodisch sind, wird zur Umkehrung der Definitionsbereich von Sekans auf … Deutsch Wikipedia