- Kreis (Geometrie)
-
 Leonardo da Vincis: Der vitruvianische Mensch - Der Mensch im Mittelpunkt eines Kreises und eines Quadrates. Der Nabel des Menschen ist der Mittelpunkt des Kreises.
Leonardo da Vincis: Der vitruvianische Mensch - Der Mensch im Mittelpunkt eines Kreises und eines Quadrates. Der Nabel des Menschen ist der Mittelpunkt des Kreises.
Der Begriff Kreis gehört zu den wichtigsten Begriffen der euklidischen Geometrie. Ein Kreis ist definiert als Menge aller Punkte der euklidischen Ebene, deren Abstand von einem vorgegebenen Punkt, dem Mittelpunkt, gleich einer festen positiven reellen Zahl, dem Radius, ist. Diese Definition entspricht dem Zeichnen eines Kreises mit dem Zirkel. Die Menge aller Punkte, die durch den Kreis umschlossen werden, wird Kreisscheibe genannt.
Ein Kreis ist ein Spezialfall eines Kegelschnitts, nämlich eine Ellipse, deren beide Brennpunkte zusammenfallen.
Inhaltsverzeichnis
Begriffsbestimmungen
Definitionen
Formal ausgedrückt lautet die Definition für einen Kreis k in der Ebene E mit Mittelpunkt
 und Radius r > 0
und Radius r > 0Dabei bezeichnet
 die Länge der Strecke [MX]. Der doppelte Radius heißt Durchmesser und wird oft mit d bezeichnet. Einen Kreis mit Radius 1 nennt man Einheitskreis.
die Länge der Strecke [MX]. Der doppelte Radius heißt Durchmesser und wird oft mit d bezeichnet. Einen Kreis mit Radius 1 nennt man Einheitskreis.Radius r und Durchmesser d bezeichnen hier positive reelle Zahlen, die durch die Beziehungen d = 2r oder r = d / 2 miteinander verknüpft sind. Andererseits wird aber auch jede Strecke, die den Mittelpunkt mit einem Punkt auf der Kreislinie verbindet, als Radius bezeichnet, und jede Strecke, die durch den Mittelpunkt geht deren beide Endpunkte auf der Kreislinie liegen, als Durchmesser. Bei dieser Sprechweise ist die Zahl r die Länge jedes Radius und die Zahl d die Länge jedes Durchmessers.
Kreisfläche
Nach der gegebenen Definition ist ein Kreis eine Kurve, also ein eindimensionales Gebilde, und keine zweidimensionale Fläche. Da das Wort „Kreis“ aber oft ungenau für die eingeschlossene Fläche benutzt wird, verwendet man zur Verdeutlichung häufig die Begriffe Kreislinie oder Kreisrand anstatt Kreis – im Gegensatz zur Kreisfläche
 . Diese ist definiert als die Menge aller Punkte der Ebene, deren Abstand von M höchstens r ist. Oft verwendet man hierfür auch das Wort (geschlossene) Kreisscheibe. Das Innere dieser Fläche heißt dann offene Kreisscheibe. Ihre Punkte haben von M einen Abstand kleiner als r:
. Diese ist definiert als die Menge aller Punkte der Ebene, deren Abstand von M höchstens r ist. Oft verwendet man hierfür auch das Wort (geschlossene) Kreisscheibe. Das Innere dieser Fläche heißt dann offene Kreisscheibe. Ihre Punkte haben von M einen Abstand kleiner als r:  .
.Kreisbogen, Kreissektor und Kreissegment
Eine zusammenhängende Teilmenge des Kreises (also der Kreislinie) ist ein Kreisbogen. Eine Verbindungsstrecke zweier Punkte der Kreislinie bezeichnet man als Kreissehne. Die längsten Kreissehnen sind diejenigen, die durch den Mittelpunkt verlaufen, also die Durchmesser. Ein Kreissektor (Kreisausschnitt) ist eine Fläche, die von zwei Radien und dem dazwischen liegenden Kreisbogen begrenzt wird. Bilden diese zwei Radien einen Durchmesser, so wird dieses auch als Halbkreis bezeichnet. Kreissegmente (Kreisabschnitte) werden von einem Kreisbogen und einer Kreissehne eingeschlossen.
Tangente, Passante und Sekante
Für die Lage einer Geraden in Bezug auf einen gegebenen Kreis gibt es drei Möglichkeiten:
- Falls der Abstand des Kreismittelpunkts von der Geraden größer ist als der Kreisradius, dann haben Kreis und Gerade keinen Punkt gemeinsam. In diesem Fall bezeichnet man die Gerade als Passante. Diese Bezeichnung hat keinen lateinischen Ursprung, aber italienisch passare = vorbeigehen.
- Stimmt der Abstand des Mittelpunkts zu der Geraden mit dem Radius überein, so gibt es genau einen gemeinsamen Punkt. Man sagt, dass die Gerade den Kreis berührt und nennt die Gerade eine Tangente (lateinisch tangere = berühren). Eine Tangente steht im Berührpunkt senkrecht (orthogonal, normal) zum entsprechenden Radius.
- Ist der Abstand zwischen Mittelpunkt und Gerade kleiner als der Kreisradius, so haben Kreis und Gerade zwei (verschiedene) Schnittpunkte und man nennt die Gerade Sekante (lateinisch secare = schneiden). Manchmal bezeichnet man den Spezialfall einer Sekante, die durch den Mittelpunkt eines Kreises verläuft als Zentrale.
Geschichte
Zeit der Ägypter und Babylonier
Schon zweitausend Jahre vor Christus beschäftigten sich die Ägypter in ihren Studien zur Geometrie mit dem Kreis. Die Kreiszahl π war ihnen unbekannt, jedoch hatten sie eine Formel entwickelt, mit deren Hilfe sie den Flächeninhalt A des Kreises näherungsweise bestimmen konnten. Sie zogen vom Durchmesser d ein Neuntel seiner Länge ab und multiplizierten das Ergebnis mit sich selbst. Sie rechneten also
und bestimmten so näherungsweise den Flächeninhalt einer Kreisfläche. Diese Informationen wurden in der altägyptischen Abhandlung Papyrus Rhind gefunden.[1] Die Babylonier (1900 bis 1600 vor Christus) kannten eine ganz andere Methode, um den Flächeninhalt der Kreisscheibe zu berechnen. Im Gegensatz zu den Ägyptern gingen sie vom Kreisumfang U aus, den sie als drei mal den Kreisdurchmesser d schätzten. Der Flächeninhalt wurde dann auf ein Zwölftel des Quadrates des Umfanges geschätzt, also[2]
Die Babylonier beschäftigten sich auch schon mit Kreissegmenten, die von einer Sehne abgeschnitten wurden. Sie konnten die Länge der Sehne oder die Höhe des Kreissegments (die senkrecht auf der Sehnenmitte stehende Strecke zwischen Sehne und Umfang) berechnen.[3]
Antike
Die Griechen werden meist als die Begründer der Wissenschaft von der Natur angesehen. Als der erste bedeutende Philosoph dieser Zeit, der sich mit Mathematik beschäftigte, gilt Thales von Milet. Er brachte Wissen über die Geometrie aus Ägypten mit nach Griechenland, wie zum Beispiel die Aussage, dass der Durchmesser den Kreis halbiert. Andere Aussagen zur Geometrie wurden von Thales selbst aufgestellt. Der heute nach Thales benannte Satz besagt, dass Peripheriewinkel im Halbkreis rechte Winkel sind. Insbesondere war Thales der erste, bei dem der Begriff des Winkels auftrat.[4]
Zirka 300 Jahre vor Christus lebte der griechische Mathematiker Euklid von Alexandria. Über ihn selbst ist wenig bekannt, aber sein Werk im Bereich der Geometrie war beachtlich. Sein Name ist heute noch in Zusammenhängen wie euklidischer Raum, euklidische Geometrie oder euklidische Metrik in Gebrauch. Sein wichtigstes Werk waren Die Elemente, eine dreizehnbändige Abhandlung, in der er die Arithmetik und Geometrie seiner Zeit zusammenfasste und systematisierte. Er folgerte die mathematischen Aussagen aus Postulaten und begründete damit die euklidische Geometrie. Der dritte Band der Elemente beschäftigte sich mit der Lehre über den Kreis.[5]
Von Archimedes, der vermutlich zwischen 287 v. Chr. 212 v. Chr. auf Sizilien lebte, ist eine ausführliche Abhandlung mit dem Titel Kreismessung überliefert.[6] Er bewies in dieser Arbeit, dass der Flächeninhalt eines Kreises gleich dem Flächeninhalt eines rechtwinkligen Dreiecks mit dem Kreisradius als der einen und dem Kreisumfang als der anderen Kathete ist. Der Flächeninhalt des Kreises lässt sich also als ½ · Radius · Umfang angeben. Mit dieser Erkenntnis führte er das Problem der Quadratur des Kreises auf die Frage der Konstruierbarkeit des Umfangs aus dem vorgegebenen Radius zurück. In seiner Abhandlung Kreismessung konnte Archimedes ebenfalls zeigen, dass der Umfang eines Kreises größer als 310/71 und kleiner als 31/7 des Durchmessers ist. Für praktische Zwecke wird diese Näherung 22/7 (~3.143) heute noch verwendet. Aus diesen beiden Aussagen folgert man, dass sich der Flächeninhalt eines Kreises zum Quadrat seines Durchmessers nahezu wie 11/14 verhält. Euklid war bereits bekannt, dass sich der Flächeninhalt eines Kreises proportional zum Quadrat seines Durchmessers verhält.[7] Archimedes gibt hier eine gute Näherung der Proportionalitätskonstante an.
In einer weiteren Arbeit Über Spiralen[6] beschreibt Archimedes die Konstruktion der später nach ihm benannten archimedischen Spirale. Mit dieser Konstruktion war es Archimedes möglich, den Umfang eines Kreises auf einer Geraden abzutragen. Auf diese Weise konnte nun der Flächeninhalt eines Kreises exakt bestimmt werden. Jedoch kann diese Spirale nicht mit Zirkel und Lineal konstruiert werden.[8]
Apollonios von Perge lebte zirka 200 Jahre vor Christus. Er knüpfte in seinem Werk „Conica“ an seine Vorgänger Euklid und Archimedes an. Nach ihm ist das apollonische Problem benannt, zu drei gegebenen Kreisen mit den euklidischen Werkzeugen Lineal und Zirkel die Kreise zu konstruieren, die die gegebenen berühren. Jedoch im Vergleich zu Euklids Elementen, die auch im Mittelalter die Grundlage der Geometrie bildeten, fanden die Werke von Apollonios zunächst nur im islamischen Bereich Beachtung. In Westeuropa erlangten seine Bücher erst im 17. Jahrhundert größere Bedeutung, als Johannes Kepler die Ellipse als die wahre Bahn eines Planeten um die Sonne erkannte.[9]
Renaissance
In der Wissenschaftsgeschichte nennt man den Zeitraum zwischen 1400 n. Chr. und 1630 n. Chr. üblicherweise Renaissance, auch wenn der zeitliche Abschnitt nicht mit der Periodisierung etwa der Kunstgeschichte übereinstimmt. In dieser Zeit fanden Euklids Elemente wieder mehr Beachtung. Sie gehörten zu den ersten gedruckten Büchern und wurden in den darauffolgenden Jahrhunderten in vielen verschiedenen Ausgaben verlegt. Erhard Ratdolt stellte 1482 in Venedig die erste gedruckte Ausgabe der Elemente her. Eine der bedeutendsten Ausgaben von Euklids Elementen wurde von dem Jesuiten Christoph Clavius herausgegeben. Er fügte den eigentlichen Texten Euklids neben den spätantiken Büchern XIV und XV noch ein sechzehntes Buch und weitere umfangreiche Ergänzungen hinzu. Beispielsweise ergänzte er eine Konstruktion der gemeinsamen Tangenten zweier Kreise.[10]
19. Jahrhundert
Nach Vorleistungen von Leonard Euler, der die eulersche Identität aufstellte, Johann Heinrich Lambert und Charles Hermite konnte Ferdinand von Lindemann 1882 beweisen, dass die Zahl π transzendent ist. Das heißt, es gibt keine Polynomfunktion mit rationalen Koeffizienten, für die π eine Nullstelle ist. Da jedoch schon im 17. Jahrhundert gezeigt wurde, dass die Kreiszahl π eine Nullstelle einer solchen Polynomfunktion sein müsse, damit die Quadratur des Kreises mit Zirkel und Lineal funktioniere, wurde somit zugleich bewiesen, dass es kein solches Verfahren geben kann.[11]
Gleichungen
Koordinatengleichung
In der analytischen Geometrie werden geometrische Objekte meistens mit Hilfe eines kartesischen Koordinatensystems beschrieben. Der Abstand eines Punktes X = (x,y) vom Punkt M = (xM,yM) berechnet sich nach dem Satz des Pythagoras als
Durch Quadrieren der definierenden Gleichung
 ergibt sich die Koordinatengleichung
ergibt sich die Koordinatengleichungfür die Punkte (x,y) auf dem Kreis mit Mittelpunkt M = (xM,yM) und Radius r. Ein wichtiger Spezialfall ist die Koordinatengleichung des Einheitskreises
Funktionsgleichung
Da der Kreis kein Funktionsgraph ist, lässt er sich auch nicht durch eine Funktionsgleichung darstellen. Behelfsweise kann ein Paar von Funktionsgleichungen
verwendet werden. Für den Einheitskreis vereinfacht sich dieses zu
Parameterdarstellung
Eine andere Möglichkeit, einen Kreis durch Koordinaten zu beschreiben, bietet die Parameterdarstellung (siehe auch Polarkoordinaten):
Hier werden die Koordinaten x und y durch den Parameter φ ausgedrückt, der alle Werte mit
 annehmen kann.
annehmen kann.Wendet man auch diese Gleichungen speziell auf den Einheitskreis an, so erhält man:
Komplexe Darstellung
In der komplexen Zahlenebene lässt sich der Kreis um
 mit Radius r > 0 durch die Gleichung
mit Radius r > 0 durch die Gleichungdarstellen. Mit Hilfe der komplexen Exponentialfunktion erhält man die Parameterdarstellung
 .
.
Kreisberechnung
Kreiszahl
Da alle Kreise ähnlich sind, ist das Verhältnis von Kreisumfang und Kreisdurchmesser für alle Kreise konstant. Der Zahlenwert dieses Verhältnisses wird in der Elementargeometrie als Definition für die Kreiszahl
 verwendet. Es handelt sich hierbei um eine transzendente Zahl, bei der sich außerdem gezeigt hat, dass sie in vielen Bereichen der Höheren Mathematik eine herausragende Bedeutung besitzt.
verwendet. Es handelt sich hierbei um eine transzendente Zahl, bei der sich außerdem gezeigt hat, dass sie in vielen Bereichen der Höheren Mathematik eine herausragende Bedeutung besitzt.Umfang
Im Rahmen der Elementargeometrie ist π das Verhältnis von Kreisumfang U zu dessen Durchmesser, und zwar für beliebige Kreise. Somit gilt
Kreisfläche
Der Flächeninhalt der Kreisfläche A (lat. area: Fläche) ist proportional zum Quadrat des Radius r bzw. des Durchmessers d des Kreises. Man bezeichnet ihn auch als Kreisinhalt.
Um die Formel für den Kreisinhalt zu erhalten, sind Grenzwert-Betrachtungen unerlässlich. Recht anschaulich ergibt sich eine solche aus der nebenstehenden Zeichnung: Die Kreisfläche ist zerlegungsgleich mit der Fläche der rechten Figur. Diese nähert sich – bei feiner werdender Sektoreinteilung – einem Rechteck an mit der Länge
 und der Breite r. Die Flächenformel ist somit
und der Breite r. Die Flächenformel ist somitDie Flächenformel kann zum Beispiel durch Integrieren der Kreisgleichung oder mit Hilfe der unten beschriebenen Annäherung durch regelmäßige Vielecke bewiesen werden.
Durchmesser
Der Durchmesser d eines Kreises mit Flächeninhalt A und mit Radius r lässt sich durch
berechnen.
Krümmung
Eine im Vergleich zu den bis jetzt beschriebenen Größen weniger elementare Eigenschaft des Kreises ist die Krümmung. Zur präzisen Definition der Krümmung werden Begriffe aus der Analysis benötigt, sie lässt sich jedoch aufgrund der Symmetrieeigenschaften des Kreises einfach berechnen. Anschaulich gibt die Krümmung in jedem Punkt P an, wie stark der Kreis in der unmittelbaren Umgebung des Punktes P von einer Geraden abweicht. Die Krümmung κ des Kreises im Punkt P lässt sich durch
berechnen, wobei r wieder der Radius des Kreises ist. Im Gegensatz zu anderen mathematischen Kurven hat der Kreis in jedem Punkt die gleiche Krümmung. Außer dem Kreis hat nur noch die Gerade eine konstante Krümmung κ = 0. Bei allen anderen Kurven ist die Krümmung vom Punkt P abhängig.
Weitere Formeln
Siehe auch: Formelsammlung GeometrieIn den folgenden Formeln bezeichnet α den Sektorwinkel im Bogenmaß. Bezeichnet α' den Winkel im Gradmaß, so gilt die Umrechnung
 .
.Formeln zum Kreis Fläche eines Kreisringes 
Länge eines Kreisbogens LB = rα Fläche Kreissektor 
Fläche eines Kreissegments 
Länge Kreissehne 
Höhe (Kreissegment) 
Trägheitsmoment (Kreisscheibe um Mittelpunkt) 
Näherungsrechnungen
Die Näherungsrechnungen für Kreisumfang und -fläche liefern zugleich Näherungen für den Zahlenwert von π:
Annäherung durch Quadrate
Ein Kreis mit Radius r wird mit einem Quadrat der Seitenlänge 2r umschrieben. Ihm wird weiter ein Quadrat mit der Diagonalen 2r einbeschrieben. Die Fläche des äußeren Quadrates ist 4r2, die des inneren nach der Dreiecksflächenformel 2r2 – der Mittelwert somit 3r2. Damit wird die Kreisfläche mit einem relativen Fehler kleiner als 5% genau bestimmt.
Auszählen in einem Raster
Die Kreisfläche lässt sich annähernd bestimmen, indem man ihr viele kleine Quadrate unterlegt (z. B. mit Millimeterpapier). Zählt man alle Quadrate, die vollständig innerhalb des Kreises liegen, so erhält man einen etwas zu niedrigen Wert für die Fläche, zählt man auch alle Quadrate mit, die den Kreis lediglich schneiden, so ist der Wert zu groß. Der Mittelwert beider Ergebnisse ergibt eine Näherung für den Flächeninhalt des Kreises, deren Güte mit der Feinheit des Quadratrasters steigt.
Annäherung durch Vielecke
Bei einer anderen Möglichkeit zur Kreisflächenbestimmung ist in den Kreis ein regelmäßiges Sechseck einzuzeichnen, dessen Ecken auf dem Kreis liegen. Werden nun die Seitenmitten vom Mittelpunkt aus auf den Kreis projiziert und diese neuen Punkte mit den alten Ecken verbunden, so entsteht ein regelmäßiges Zwölfeck. Wird dieser Vorgang wiederholt, entstehen nacheinander ein 24-Eck, ein 48-Eck und so fort.
In jedem Sechseck sind die Seiten gleich lang wie der Umkreisradius. Die Seiten der folgenden Vielecke ergeben sich mit Hilfe des Satzes von Pythagoras jeweils aus den Seiten der vorhergehenden. Aus den Seiten lassen sich die Flächen der Vielecke durch Dreiecksflächenberechnung exakt bestimmen. Sie sind alle etwas kleiner als die Kreisfläche, der sie sich bei steigender Eckenzahl jedoch annähern.
Entsprechend kann man mit einem Sechseck verfahren, das von außen an den Kreis gezeichnet ist, dessen Seitenmitten also auf ihm liegen. Man erhält eine fallende Folge von Flächenmaßen, deren Grenzwert wiederum die Kreisfläche ist.
Geometrische Sätze und Begriffe rund um den Kreis
Symmetrie und Abbildungseigenschaften
Der Kreis ist eine geometrische Figur von sehr hoher Symmetrie. Jede Gerade durch seinen Mittelpunkt ist eine Symmetrieachse. Zudem ist der Kreis rotationssymmetrisch, d. h., jede Drehung um den Mittelpunkt bildet den Kreis auf sich selbst ab. In der Gruppentheorie werden die genannten Symmetrieeigenschaften des Kreises durch seine Symmetriegruppe charakterisiert. Formal ergibt sich dafür die orthogonale Gruppe O(2), das ist die Gruppe der orthogonalen
 -Matrizen.
-Matrizen.Alle Kreise mit dem gleichen Radius sind zueinander kongruent, lassen sich also durch Parallelverschiebungen aufeinander abbilden. Zwei beliebige Kreise sind zueinander ähnlich. Sie lassen sich stets durch eine zentrische Streckung und eine Parallelverschiebung aufeinander abbilden.
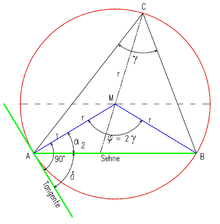
Kreiswinkel und Winkelsätze
Eine Kreissehne mit Endpunkten A und B teilt einen gegebenen Kreis in zwei Kreisbögen. Ein Winkel
 mit Scheitel C auf einem der Kreisbögen wird Umfangswinkel oder Peripheriewinkel genannt. Der Winkel
mit Scheitel C auf einem der Kreisbögen wird Umfangswinkel oder Peripheriewinkel genannt. Der Winkel  mit Scheitel im Mittelpunkt M heißt Mittelpunktswinkel oder Zentriwinkel.
mit Scheitel im Mittelpunkt M heißt Mittelpunktswinkel oder Zentriwinkel.Im Spezialfall, dass die Sehne den Mittelpunkt enthält, also ein Durchmesser des Kreises ist, ist der Mittelpunktswinkel ein gestreckter Winkel mit 180°. In dieser Situation gilt eine grundlegende Aussage der Kreisgeometrie, der Satz von Thales: Er besagt, dass Umfangswinkel über einem Durchmesser stets rechte Winkel sind, also 90° betragen. Der Kreis um das rechtwinklige Dreieck wird in dieser Situation auch Thaleskreis genannt.
Auch im Fall einer beliebigen Kreissehne sind alle Umfangswinkel, die auf dem gleichen Kreisbogen liegen, gleich groß. Diese Aussage wird auch Umfangswinkelsatz genannt. Der Kreisbogen, auf dem die Scheitel der Umfangswinkel liegen, heißt Fasskreisbogen. Liegen Umfangswinkel und Zentriwinkel auf der gleichen Seite der Sehne, dann ist der Zentriwinkel doppelt so groß wie der Umfangswinkel (Kreiswinkelsatz). Zwei Umfangswinkel, die auf gegenüberliegenden Seiten der Sehne liegen, ergänzen sich zu 180°.
Der Umfangswinkel ist genauso groß wie der spitze Sehnentangentenwinkel zwischen der Sehne und der durch einen ihrer Endpunkte verlaufenden Tangente (Sehnentangentenwinkelsatz).
Sätze über Sehnen, Sekanten und Tangenten
Für Kreise gilt der Sehnensatz, der besagt: Schneiden zwei Sehnen [AC] und [BD] einander in einem Punkt S, so gilt
d. h., die Produkte der jeweiligen Sehnenabschnitte sind gleich.
Zwei Sehnen eines Kreises, die sich nicht schneiden, können verlängert werden zu Sekanten, die entweder parallel sind oder sich in einem Punkt S außerhalb der Kreises schneiden. Ist letzteres der Fall, so gilt analog zum Sehnensatz der Sekantensatz
Im Fall einer Sekante, die den Kreis in den Punkte A und C schneidet, und einer Tangente, die den Kreis im Punkt B berührt, gilt der Sekanten-Tangenten-Satz: Ist S der Schnittpunkt von Sekante und Tangente, so folgt
Umkreise und Inkreise
Sind A, B, C drei Punkte, die nicht auf einer Geraden liegen, also ein nicht ausgeartetes Dreieck bilden, dann existiert ein eindeutig bestimmter Kreis durch diese Punkte, nämlich der Umkreis des Dreiecks ABC. Der Mittelpunkt des Umkreises ist der Schnittpunkt der drei Mittelsenkrechten des Dreiecks. Ebenso kann jedem Dreieck ein eindeutig bestimmter Kreis einbeschrieben werden, der die drei Seiten berührt, d. h., die Dreiecksseiten bilden Tangenten des Kreises. Dieser Kreis wird Inkreis des Dreiecks genannt. Sein Mittelpunkt ist der Schnittpunkt der drei Winkelhalbierenden.
In der Elementargeometrie werden noch weitere Kreise am Dreieck betrachtet: Die Ankreise liegen außerhalb des Dreiecks und berühren eine Seite und die Verlängerungen der beiden anderen Seiten. Ein weiterer interessanter Kreis am Dreieck ist der Feuerbachkreis, benannt nach Karl Wilhelm Feuerbach. Auf ihm liegen die drei Seitenmittelpunkte und die drei Fußpunkte der Höhen. Da auf ihm außerdem die drei Mittelpunkte der Strecken zwischen dem Höhenschnittpunkt und den Ecken des Dreiecks liegen, wird der Feuerbachkreis auch Neunpunktekreis genannt. Sein Mittelpunkt liegt wie der Schwerpunkt, der Umkreismittelpunkt und der Höhenschnittpunkt auf der eulerschen Geraden.
Im Gegensatz zu Dreiecken besitzen Polygone mit mehr als drei Ecken im Allgemeinen keinen Umkreis oder Inkreis. Für regelmäßige Vielecke existieren beide allerdings stets. Ein Viereck, das einen Umkreis besitzt, wird Sehnenviereck genannt. Ein konvexes Viereck ist genau dann ein Sehnenviereck, wenn sich gegenüberliegende Winkel zu 180° ergänzen. Ein Viereck, das einen Inkreis besitzt, wird Tangentenviereck genannt. Ein konvexes Viereck ist genau dann ein Tangentenviereck, wenn die Summe der Seitenlängen zweier gegenüberliegender Seiten gleich der Summe der beiden anderen Seitenlängen ist.
Kreisspiegelungen und Möbiustransformationen
Die Kreisspiegelung, auch Inversion genannt, ist eine spezielle Abbildung der ebenen Geometrie, die eine „Spiegelung“ der euklidischen Ebene an einem gegebenen Kreis k mit Mittelpunkt M und Radius r beschreibt. Ist
 ein gegebener Punkt, dann ist sein Bildpunkt P' dadurch bestimmt, dass er auf der Halbgeraden [MP liegt und sein Abstand von M die Gleichung
ein gegebener Punkt, dann ist sein Bildpunkt P' dadurch bestimmt, dass er auf der Halbgeraden [MP liegt und sein Abstand von M die Gleichungerfüllt. Die Kreisspiegelung bildet das Innere des gegebenen Kreises k auf sein Äußeres ab und umgekehrt. Alle Kreispunkte von k werden auf sich selbst abgebildet. Kreisspiegelungen sind winkeltreu, orientierungsumkehrend und kreistreu. Letzteres bedeutet, dass verallgemeinerte Kreise – das sind Kreise und Geraden – wieder auf verallgemeinerte Kreise abgebildet werden.
Die Hintereinanderausführung zweier Kreisspiegelungen ergibt eine Möbiustransformation. Möbiustransformationen – eine weitere wichtige Klassen von Abbildungen der Ebene – sind daher ebenfalls winkeltreu und kreistreu, allerdings orientierungserhaltend.
Kreisspiegelungen und Möbiustransformationen lassen sich besonders übersichtlich mit Hilfe komplexer Zahlen darstellen: Bei einer Kreisspiegelung eines Punktes
 an dem Kreis
an dem Kreis  lautet die Formel für den Bildpunkt
lautet die Formel für den Bildpunkt 
Für die Spiegelung am Einheitskreis gilt einfach
 .
.Möbiustransformationen der komplexen Ebene werden durch gebrochen lineare Funktionen der Gestalt
mit
 und
und  dargestellt.Siehe auch: Potenz (Geometrie)
dargestellt.Siehe auch: Potenz (Geometrie)Konstruktionen mit Zirkel und Lineal
Ein klassisches Problem der Geometrie ist die Konstruktion geometrischer Objekte mit Zirkel und Lineal in endlich vielen Konstruktionsschritten aus einer gegebenen Punktemenge. In jedem Schritt dürfen dabei Geraden durch gegebene oder bereits konstruierte Punkte gezogen werden sowie Kreise um solche Punkte mit gegebenem oder bereits konstruiertem Radius gezogen werden. Die dadurch konstruierten Punkte ergeben sich als Schnittpunkte zweier Geraden, zweier Kreise oder einer Geraden mit einem Kreis. Naturgemäß spielen daher bei allen Konstruktionen mit Zirkel und Lineal Kreise eine wichtige Rolle.
Im Folgenden sollen exemplarisch einige Konstruktionen angesprochen werden, die im Zusammenhang mit der Geometrie von Kreisen von Bedeutung sind.
Thaleskreis
Für die Konstruktion des Thaleskreises über einer gegebenen Strecke [AB] wird zunächst der Mittelpunkt M dieser Strecke konstruiert, der auch der Mittelpunkt des Thaleskreises ist. Dazu werden um A und B Kreise mit dem gleichen Radius r geschlagen, wobei r so groß gewählt werden muss, dass die beiden Kreise sich in zwei Punkten C und D schneiden. Das ist z. B. für
 der Fall. Die Gerade CD schneidet dann [AB] im Mittelpunkt M. Der gesuchte Thaleskreis ist nun der Kreis mit Mittelpunkt M und Radius
der Fall. Die Gerade CD schneidet dann [AB] im Mittelpunkt M. Der gesuchte Thaleskreis ist nun der Kreis mit Mittelpunkt M und Radius  .
.Konstruktion von Tangenten
Gegeben sei ein Punkt P außerhalb eines Kreises k mit Mittelpunkt M und es sollen die beiden Tangenten an den Kreis konstruiert werden, die durch den Punkt P laufen. Diese elementare Konstruktionsaufgabe lässt sich einfach mit Hilfe des Satzes von Thales lösen: Man konstruiert den Thaleskreis mit der Strecke [PM] als Durchmesser. Die Schnittpunkte dieses Kreises mit k sind dann die Berührpunkte der gesuchten Tangenten.
Flächenverdoppelung
Die Fläche eines Kreises lässt sich geometrisch verdoppeln, indem ein Quadrat gezeichnet wird, dessen eine Ecke im Kreismittelpunkt liegt, wobei zwei weitere Ecken auf dem Kreisbogen liegen. Durch die vierte Ecke wird ein Kreis um den alten Mittelpunkt gezogen. Dieses Verfahren wurde im 13. Jahrhundert im Bauhüttenbuch des Villard de Honnecourt dargestellt. Dieses Verfahren funktioniert, da (nach dem Satz des Pythagoras)
und damit der Flächeninhalt des großen Kreises
genau doppelt so groß ist, wie der des kleinen Kreises.
Kreisteilung
Ein weiteres bereits in der Antike untersuchtes Konstruktionsproblem ist die Kreisteilung. Hierbei soll zu einer gegebenen natürlichen Zahl n einem gegebenen Kreis ein regelmäßiges n-Eck einbeschrieben werden. Die auf dem Kreis gelegenen Eckpunkte teilen diesen dann in n gleich lange Kreisbögen. Diese Konstruktion ist nicht für alle n möglich: Mit Hilfe der algebraischen Theorie der Körpererweiterungen lässt sich zeigen, dass sie genau dann durchführbar ist, wenn n eine Primfaktorzerlegung der Form
hat mit
 und paarweise verschiedenen fermatsche Primzahlen
und paarweise verschiedenen fermatsche Primzahlen  , also Primzahlen der Form
, also Primzahlen der Form  . Damit ist die Konstruktion also beispielsweise für n = 3,4,5,6,8,10,12,15,16,17 möglich, jedoch nicht für z. B. n = 7,9,11,13,14. Die Konstruktion des regelmäßigen Siebzehnecks gelang Carl Friedrich Gauß im Jahr 1796.
. Damit ist die Konstruktion also beispielsweise für n = 3,4,5,6,8,10,12,15,16,17 möglich, jedoch nicht für z. B. n = 7,9,11,13,14. Die Konstruktion des regelmäßigen Siebzehnecks gelang Carl Friedrich Gauß im Jahr 1796.Konstruktion im digitalen Raster
Den Bresenham-Algorithmus gibt es in einer Variante zur Kreisgenerierung (siehe dort bei Kreisvariante). Dabei werden nur Grundrechenarten verwendet, um einen Kreis auf einem Punktraster zu erzeugen.
Kreisberechnung in der Analysis
In der modernen Analysis werden die trigonometrischen Funktionen und die Kreiszahl π üblicherweise zunächst ohne Rückgriff auf die elementargeometrische Anschauung und auf spezielle Eigenschaften des Kreises definiert. So lassen sich etwa Sinus und Kosinus über ihre Darstellung als Potenzreihe definieren. Eine gängige Definition für den Wert von π ist dann das Doppelte der kleinsten positiven Nullstelle des Kosinus.
Der Kreis als Kurve
In der Differentialgeometrie, einem Teilgebiet der Analysis, das geometrische Formen mit Hilfe der Differential- und Integralrechnung untersucht, werden Kreise als spezielle Kurven angesehen. Diese Kurven lassen sich mit Hilfe der oben genannten Parameterdarstellung als Weg beschreiben. Legt man den Koordinatenursprung in den Mittelpunkt eines Kreises mit Radius r, dann ist durch die Funktion
![f \colon [0, 2\pi] \to \R^2](7/b17e2575b9ca02d9501000d5db1c134e.png) mit
miteine solche Parametrisierung gegeben. Mit Hilfe der trigonometrischen Formel sin 2t + cos 2t = 1 folgt für die euklidische Norm der parametrisierten Punkte | f(t) | = r, das heißt, sie liegen tatsächlich auf einem Kreis mit Radius r. Da Sinus und Kosinus 2π-periodische Funktionen sind, entspricht das Definitionsintervall [0,2π] von f genau einem Kreisumlauf.
Kreisumfang
Der Umfang des Kreises ergibt sich als Länge des Weges f durch Integration zu
Analog gilt für die Länge s(t) des durch f | [0,t] gegebenen Teilkreisbogens s(t) = rt. Dadurch erhält man als Parametrisierung des Kreises nach der Bogenlänge
mit
![s \in [0,2\pi r]](7/80799e984192f8617e0ab4ebb1a1a03d.png) .
.Flächeninhalt
Der Flächeninhalt A der Kreisscheibe
 , also das Maß der Menge K, kann als (zweidimensionales) Integral
, also das Maß der Menge K, kann als (zweidimensionales) Integraldargestellt werden. Um die etwas mühsame Berechnung dieses Integrals in kartesischen Koordinaten zu umgehen, ist es günstig, eine Transformation x = ρcos φ, y = ρsin φ auf Polarkoordinaten zu verwenden. Damit ergibt sich
Eine andere Möglichkeit zur Berechnung der Kreisfläche besteht darin, die Sektorformel von Leibniz auf die Parameterdarstellung des Kreisrandes anzuwenden. Mit x(t) = rcos t, y(t) = rsin t erhält man damit ebenfalls
Krümmung
Für die oben hergeleitete Parametrisierung
 des Kreises nach seiner Bogenlänge ergibt sich
des Kreises nach seiner Bogenlänge ergibt sichFür die Krümmung des Kreises erhält man daher
Die Krümmung des Kreises ist also konstant und der Krümmungsradius
 ist gerade sein Radius.
ist gerade sein Radius.In der Differentialgeometrie wird gezeigt, dass eine ebene Kurve bis auf Kongruenz durch ihre Krümmung eindeutig bestimmt ist. Die einzigen ebenen Kurven mit konstanter positiver Krümmung sind daher Kreisbögen. Im Grenzfall, dass die Krümmung konstant gleich 0 ist, ergeben sich Geradenstücke.
Isoperimetrisches Problem
Unter allen Flächen der euklidischen Ebene mit gegebenem Umfang besitzt die Kreisfläche den größten Flächeninhalt. Umgekehrt hat die Kreisfläche bei gegebenem Flächeninhalt den kleinsten Umfang. In der Ebene ist der Kreis daher die eindeutig bestimmte Lösung des sog. isoperimetrischen Problems. Obwohl diese anschaulich einleuchtende Tatsache schon den Mathematikern im antiken Griechenland bekannt war, wurden formale Beweise erst im 19. Jahrhundert erbracht. Da eine Kurve gesucht ist, die ein Funktional maximiert, nämlich den umschlossenen Flächeninhalt, handelt es sich dabei aus moderner Sicht um ein Problem der Variationsrechnung. Ein gängiger Beweis für stückweise stetige Kurven verwendet die Theorie der Fourierreihen.[12]
Verallgemeinerungen
Kegelschnitte
In der ebenen Geometrie kann der Kreis als spezielle Ellipse aufgefasst werden, bei dem die beiden Brennpunkte mit dem Kreismittelpunkt zusammenfallen. Beide Halbachsen sind dabei gleich dem Kreisradius. Der Kreis ist daher ein spezieller Kegelschnitt: Er entsteht als Schnitt eines geraden Kreiskegels mit einer Ebene senkrecht zu Kegelachse. Er ist damit ein Spezialfall einer zweidimensionalen Quadrik.
Hierbei ergibt sich eine weitere, äquivalente Definition für Kreise (Kreis des Apollonios): Ein Kreis ist die Menge aller Punkte in der Ebene, für die der Quotient q ihrer Abstände von zwei gegebenen Punkten konstant ist. Die beiden Punkte liegen auf einem von M ausgehenden Strahl im Abstand r / q bzw. r * q und wechselseitig auf der Polaren des jeweils anderen Punktes als Pol. Ähnliche Definitionen gibt es auch für die Ellipse (konstante Summe), Hyperbel (konstante Differenz) und die Cassinische Kurve (konstantes Produkt der Abstände).
Sphäre
Es ist möglich, den Kreis als Objekt der Ebene in den dreidimensionalen Raum zu verallgemeinern. Dann erhält man die Hülle einer Kugel. Dieses Objekt wird in der Mathematik Sphäre oder genauer 2-Sphäre genannt. Analog lässt sich die 2-Sphäre auf n Dimensionen zur n-Sphäre verallgemeinern. In diesem Kontext nennt man den Kreis auch 1-Sphäre.
Kreise in der synthetischen Geometrie
In der synthetischen Geometrie können Kreise in bestimmten affinen Ebenen (zum Beispiel präeuklidischen Ebenen) ohne einen Abstandsbegriff allein durch eine Orthogonalitätsrelation definiert werden, indem der Satz vom Umkreis (Mittellotensatz) zur Definition des Kreises verwendet wird. Dadurch kann dann ein schwächerer Begriff der „Abstands-“ oder „Längengleichheit“ von Punktepaaren (A,B) in solchen Ebenen eingeführt werden. → Siehe dazu Präeuklidische Ebene.
Siehe auch
Literatur
- Ilka Agricola, Thomas Friedrich: Elementargeometrie. 3. Auflage, Vieweg+Teubner Verlag, Wiesbaden 2011, ISBN 978-3-8348-1385-5.
- Christian Bär: Elementare Differentialgeometrie. 2. Auflage, Walter de Gruyter, Berlin 2010, ISBN 978-3-11-022458-0.
- Hartmut Wellstein, Peter Kirsche: Elementargeometrie. Eine aufgabenorientierte Einführung. Vieweg+Teubner Verlag, Wiesbaden 2009, ISBN 978-3-8348-0856-1.
Weblinks
 Commons: Kreis – Sammlung von Bildern, Videos und Audiodateien
Commons: Kreis – Sammlung von Bildern, Videos und Audiodateien Wikibooks: Beweis der Transzendenz von e und π – im Beweisarchiv
Wikibooks: Beweis der Transzendenz von e und π – im Beweisarchiv- „Mathematische Basteleien“ zum Kreis
- Eric W. Weisstein: Kreis. In: MathWorld. (englisch)
Einzelnachweise
- ↑ Christoph J. Scriba & Peter Schreiber: 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen (Vom Zählstein zum Computer). 1. Auflage, Springer Berlin/Heidelberg/New York ISBN 3-540-67924-3, S. 13.
- ↑ Christoph J. Scriba & Peter Schreiber: 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen (Vom Zählstein zum Computer). 1. Auflage, Springer Berlin/Heidelberg/New York ISBN 3-540-67924-3, S. 18.
- ↑ Christoph J. Scriba & Peter Schreiber: 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen (Vom Zählstein zum Computer). 1. Auflage, Springer Berlin/Heidelberg/New York ISBN 3-540-67924-3, S. 19.
- ↑ Christoph J. Scriba & Peter Schreiber: 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen (Vom Zählstein zum Computer). 1. Auflage, Springer Berlin/Heidelberg/New York ISBN 3-540-67924-3, S. 31-33.
- ↑ Christoph J. Scriba & Peter Schreiber: 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen (Vom Zählstein zum Computer). 1. Auflage, Springer Berlin/Heidelberg/New York ISBN 3-540-67924-3, S. 49-50.
- ↑ a b In englischer Übersetzung von Thomas Little Heath: The works of Archimedes, ed. in modern notation, with introductory chapters. University press, Cambridge 1897. Kreismessung: S.91ff., Über Spiralen: S.151ff. (Digitalisat)
- ↑ Euklids Elemente XII, § 2.
- ↑ s. Gericke: Antike und Orient, S.120ff.
- ↑ Christoph J. Scriba & Peter Schreiber: 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen (Vom Zählstein zum Computer). 1. Auflage, Springer Berlin/Heidelberg/New York ISBN 3-540-67924-3, S. 72-73.
- ↑ Christoph J. Scriba & Peter Schreiber: 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen (Vom Zählstein zum Computer). 1. Auflage, Springer Berlin/Heidelberg/New York ISBN 3-540-67924-3, S. 247-248.
- ↑ Christoph J. Scriba & Peter Schreiber: 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen (Vom Zählstein zum Computer). 1. Auflage, Springer Berlin/Heidelberg/New York ISBN 3-540-67924-3, S. 405-406.
- ↑ Hurwitz Quelques applications geometriques des series de Fourier, Annales de l´Ecole Normale, Bd.19, 1902, S.357-408, der Beweis findet sich zum Beispiel in Blaschke Vorlesungen über Differentialgeometrie, Bd.1, Springer, 1924, S.45
Wikimedia Foundation.