- Ekliptik
-
 Die Bahnebenen aller Planeten sind nur relativ gering gegeneinander geneigt. Diese auffallende Gemeinsamkeit führte zur Erklärung der Entstehungsgeschichte des Sonnensystems
Die Bahnebenen aller Planeten sind nur relativ gering gegeneinander geneigt. Diese auffallende Gemeinsamkeit führte zur Erklärung der Entstehungsgeschichte des Sonnensystems
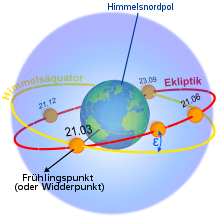
Die Ekliptik (lat. linea ecliptica, „zur Eklipse gehörende Linie/Bahn“, zu gr. ἔκλειψις, ekleipsis, „Ausbleiben, Verschwinden, Finsternis“) ist als Projektion der scheinbaren Bahn der Sonne im Verlauf eines Jahres ein imaginärer Großkreis auf der Himmelskugel, das heißt ein Kreis vor dem Fixsternhintergrund. Die von ihr definierte Ebene wird Ekliptikebene oder Ekliptikalebene genannt. Diese Bezeichnung wird vorwiegend bei heliozentrischer Betrachtung gebraucht. Sie stellt den Zusammenhang zwischen der in der Ekliptikebene liegenden Bahn der sich um die Sonne bewegenden Erde und der Ekliptik dar.
Der Winkel zwischen der vom Himmelsäquator definierten Äquatorebene und der Ekliptikebene ist die Schiefe der Ekliptik ε (Erdneigung oder auch Obliquität).
„Sonne“ und „Erde“ beziehen sich hierbei auf die mittleren Körper der Himmelsmechanik, nicht auf die tatsächlichen Himmelskörper. Insbesondere steht „Erde“ für den Erde-Mond-Schwerpunkt.
Inhaltsverzeichnis
Schiefe der Ekliptik
Die Rotationsachse der Erde, Erdachse, steht nicht senkrecht auf der Ebene der Erdbahn, sondern bildet mit ihr einen Winkel von etwa 66,56 Grad. Dadurch schließt die ekliptikale Ebene mit der Ebene des Äquators der Erde beziehungsweise des Himmelsäquators derzeit einen Winkel von 23,4385° ein, der Schiefe der Ekliptik oder Obliquität genannt wird (lat. obliquus „schief“). Die Bezeichnung Erdneigung gibt diesen Winkel unter dem Blick von der Ekliptikebene auf die Erde wieder, der Perspektive des Ekliptikalen Koordinatensystem.
Die Schiefe der Ekliptik ist eine der zehn wichtigsten Basisgrößen der Astronomie und Geodäsie zur Definition von Koordinatensystemen und für Berechnungen in der Astronomie und Geodäsie. Sie wird meist mit dem griechischen Buchstaben epsilon ε bezeichnet.
Ekliptikpol
Da die Erde von der Kugelgestalt abweicht, bewirken die Gezeitenkräfte von Mond und Sonne ein Drehmoment, das die schrägstehende Erdachse aufzurichten versucht. Die Erdachse, die auf die Himmelspole zeigt, beschreibt dadurch wie ein schräglaufender Kinderkreisel eine Präzession auf einem Kegelmantel mit Öffnungswinkel 2ε um die Ekliptikpole herum. Diese Ekliptikpole sind auf präziseren Sternkarten eingezeichnet; der nördliche Ekliptikpol befindet sich im Sternbild Drache, definitionsgemäß auf Rektaszension 18 h, der südliche im Sternbild Schwertfisch auf 6 h.
Der „Erdkreisel“ ist wegen der großen Erdmasse von knapp 6·1024 kg (6 Mio. Mrd. Mrd. Kilogramm) sehr träge, und die Erdachse braucht für einen Umlauf etwa 25.700–25.800 Jahre (ein Platonisches Jahr). Der heutige sogenannte Polarstern nimmt seine Rolle also nur vorübergehend ein.
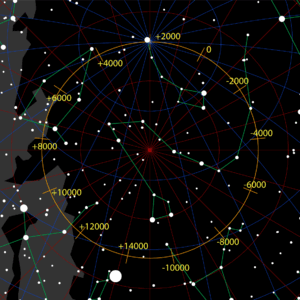 Der Weg (orange) des Himmelsnordpols um den Ekliptikpol (rot), wofür er etwa 26.000 Jahre benötigt.
Der Weg (orange) des Himmelsnordpols um den Ekliptikpol (rot), wofür er etwa 26.000 Jahre benötigt.
Um das Jahr (+)2000, sehr nahe am Polarstern.
Der helle Stern unten ist die Wega. Der Weg des Himmelssüdpols um den Ekliptikpol, wofür er etwa 26.000 Jahre benötigt.
Der Weg des Himmelssüdpols um den Ekliptikpol, wofür er etwa 26.000 Jahre benötigt.
Der helle Stern über der Bildmitte ist Canopus.Schwankung der Erdachse und mittlere Ekliptikschiefe
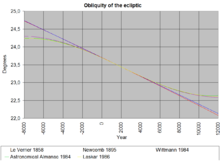
Jedoch auch der Winkel der Ekliptikschiefe ändert sich langperiodisch durch Gravitationseinflüsse der Körper im Sonnensystem aufeinander. Daher variiert ε innerhalb von 40.000 Jahren zwischen etwa 21° 55′ und 24° 18′. Dieser Effekt trägt neben der Exzentrizität (100.000 Jahre) und der Präzession (25.780 Jahre) zur Entstehung der Eiszeiten bei (als einer der Faktoren der langfristig-regelmäßigen, natürlich auftretenden Klimaschwankungen, die man Milanković-Zyklen nennt):
Als erste Näherung wird für die mittlere Ekliptikschiefe ε0 = 23° 26′ 21,45″ − 46,8″·T mit T als Zeitargument in Julianischen Jahrhunderten seit der Epoche J2000.0 angegeben[1], beträgt also:
- 23° 26′ 19,1″ oder 23,43864° (2005).
Ekliptikale Breite der Sonne
Streng genommen ist die Ekliptikalebene nicht genau die Bahnebene der Erde, sondern diejenige des Baryzentrums (Schwerpunkt) von Erde und Mond (Erde-Mond-Schwerpunkt), die sozusagen als Doppelplanet die Sonne umrunden.
Daher läuft die geozentrische Sonne (vom Erdzentrum gerechnet) nicht genau in der Ekliptik (ekliptikale Breite β = 0), sondern sie hat eine kleine ekliptikale Breite: Überlagert wird der Wert der mittleren Ekliptikschiefe im Monatsrhythmus von der Wirkung der Nutation in einer Größenordnung von Δε = ±9,21″ (Nutation in Schiefe). In der Nutation in Schiefe sind noch etwa ±0,7″ durch die Schwankungen der Erde um den Erde-Mond-Schwerpunkt eingerechnet sowie noch kleinere Schwankungen der wahren Sonne um das Baryzentrum des Sonnensystems.
Die ekliptikale Länge (im Bild λ, von 0° bis 360°) folgt etwa den Keplerschen Gesetzen plus der Nutation in Länge. Ausführlich erläutert wird dieser Aspekt unter Mittlere Länge der Erde im Artikel Tropisches Jahr.
Jahreszeiten und Ekliptikschiefe
Während die Erde jährlich die Sonne umrundet, bleibt die Stellung ihrer Achse im Raum fast unverändert, wenn man von den oben beschriebenen langperiodischen Effekten absieht. Dadurch weist in den Monaten zwischen März und September die Nordhalbkugel etwas mehr zur Sonne, in den Monaten zwischen September und März aber die Südhalbkugel. Dieser variable Einfallswinkel der Sonnenstrahlen und die damit einhergehende Änderung der Tageslänge sind die Ursachen für den Wechsel der Jahreszeiten.
Je stärker die Ekliptikschiefe, desto ausgeprägter werden die Jahreszeiten – und auch die Unterschiede zwischen dem Winter auf der Nord- und Südhalbkugel. Letztere hat strengere Winter (Juli bis September) als der Norden, weil im Juli die Erde ihren sonnenfernsten Punkt (Aphel) durchläuft. Da sich aber die „Apsidenlinie“ (Aphel – Perihel) ebenfalls langperiodisch verschiebt, genügt eine relativ kleine regionale Klimaänderung, dass sich eine Art „kalte Welle“ aufschaukelt. Dies hat möglicherweise einen Einfluss auf die Eiszeiten. Ist nämlich die Erde mehr als sonst von Eis bedeckt, strahlt dieses mehr Sonnenwärme ins Weltall zurück und kühlt noch mehr aus.
Geschichtliches zur Ekliptik-Forschung
Etymologie und frühe Konzepte
Der Name „Ekliptik“ ist abgeleitet von dem griechischen weiblichen Adjektiv ἐκλειπτική [τροχιά] ekliptikí [trochiá] ‚die verdeckende [Umlaufbahn]‘ (von έκλειψη éklιpsi wörtlich ‚Überlagerung, Verdeckung, Auslöschung‘; εκλειψις ekleïpsis ‚Finsternis, Verdunkelung‘; vergleiche Eklipse/Okkultation): Sonnen- oder Mondfinsternisse kommen nämlich nur dann vor, wenn der Neu- bzw. Vollmond nahe (partielle Finsternis) oder sehr nahe (totale oder ringförmige Finsternis) der Ekliptik steht.
Für die frühen Astronomen war intuitiv die Mondbahn die vorrangige – weil unmittelbarer zu beobachtende – Bahn, die Ekliptik aber die ‚Bahn des Drachens‘, der im Drachenpunkt, dem Mondknoten, Sonne oder Mond verschlingt. Der Zusammenhang zwischen Ekliptik und scheinbarer Bahn der Sonne wurde erst später erkannt:
Durch das geozentrische Weltbild der Antike verstand man, dass die Sonne auf der nächtlichen Rückkehr nach Osten nicht unabhängig unter der Erde durchwandert, sondern auf einer Sphäre genau den Sternen gegenüberliegt, die jeweils 12 Stunden später am jeweiligen Ort der Sonne stehen. Dadurch konnte die aus der Sternbeobachtung schon bekannte jährliche Verschiebung des Sternenhimmels damit in Zusammenhang gebracht werden, dass die Sonne auf der Ekliptik innerhalb eines Jahres um die Erde kreist (nach heutigem Verständnis natürlich als scheinbare, geozentrische Bewegung).Der Bereich beiderseits der Ekliptik, innerhalb dessen die scheinbaren Bewegungen von Sonne, Mond und Planeten verlaufen, wird Zodiak oder Tierkreis genannt. Die Fixsterne sind bezüglich der Himmelskugel praktisch bewegungslos und bilden, von der Erde aus betrachtet, die Sternbilder. Zwölf der dreizehn Sternbilder, die von der Ekliptik geschnitten werden, wurden als Grundlage der Kalenderberechnung von den antiken Sterndeutern als Tierkreiszeichen verwendet. Aufgrund der Präzession sind seit der Benennung der Tierkreiszeichen diese und die gleichnamigen Sternbilder heute aber nicht mehr deckungsgleich, sondern um etwa 30°, also ein Tierkreiszeichen verschoben. Von etwa 4000 bis 1500 v. Chr. lief der Frühlingspunkt durch das Sternbild Stier wobei er auch das Goldene Tor der Ekliptik, das durch die beiden markanten Sternhaufen der Plejaden und der Hyaden gebildet wird, passierte.
Die Einteilung der Ekliptik in zwölf gleich große Tierkreiszeichen erfolgte während der Antike. So galt die Waage lange als Teil des Skorpions. In Indien wurde die Mondbahn und somit auch die Ekliptik hingegen in 27 bzw. 28 Mondstationen (Nakshatras) aufgeteilt, ein System, welches auch von den Arabern (Manazil al-Qamar) und den Chinesen übernommen wurde. Andererseits teilten die alten Ägypter die Ekliptik in 36 Dekane ein.
Vom Altertum bis Leonhard Euler und Laplace
Einer der bedeutendste Astronomen der Blütezeit des Islams war Muhammad Ibn Dschubair al-Battani (858–929). Er bestimmte unter anderem die Schiefe der Ekliptik und die Tagundnachtgleiche. Seit etwa der Zeitenwende wissen die Astronomen, dass die Erdachse präzediert, allerdings wurde der heute bekannte Wert von 25.700 bis 25.800 Jahren erst im 13. Jahrhundert festgestellt. Dass sich außer ihrer Richtung auch die Schiefe der Ekliptik verändert, ahnte man erst im Mittelalter. Man vermutete damals, dass ihr Winkel im Lauf der Jahrtausende alle Werte von 0° bis 90° annimmt. Erst um 1600 wurde klar, dass die Schwankungsbreite viel geringer war.
Die Ursache für die Änderungen (siehe Tabelle oben) sind die anderen 7 Planeten, deren Bahnebenen von jener der Erde um 1° (Jupiter, Uranus) bis 7° (Merkur) abweichen. Sie üben wegen der Abplattung der Erde auf sie Drehmomente aus (Abweichung von der Kugelform 0,33530 % oder 21 km).
Die erste theoretische Berechnung dieser Änderung in ε gelang Leonhard Euler im Jahr 1754. Ergebnis seiner Analyse war dε/dt = −47,5″/Jh., woraus er für das Jahr 1817 ε = 23° 27′ 47,0″ prognostizierte. Als die Massen der Planeten genauer bekannt waren, wiederholte Joseph-Louis Lagrange 1774 Eulers Berechnungen, woraus er −56,2″ pro Jahrhundert und für 1817 den Wert 23° 47′ 48,0″ erhielt. 1782 kam er mit verbesserter Theorie auf −61,6″/Jh., wogegen Jérôme Lalande um 1790 in seinen Astronomie-Tafeln −33,3″/Jh. und 23° 47′ 38,9″ erhielt.
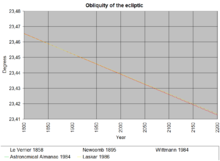
Diese doch beträchtlichen Unterschiede zwischen so hervorragenden Mathematikern veranlassten Pierre-Simon Laplace (1789–1827) zu einer noch gründlicheren Analyse, aus der ein Schwankungsbereich von ±1,358° folgte. Er weicht vom heutigen Wert nur um 0,6° (in 20 Jahrtausenden) ab. Der Mannheimer Astronom Friedrich Nicolai – ein Schüler von Carl Friedrich Gauß – errechnete für das Jahr 1800 dε/dt = −49,40″/Jh.. Auch andere berühmte Himmelsmechaniker erforschten den Verlauf dieser fundamentalen Größe, und Urbain Le Verrier publizierte 1858 die theoretische Formel
(T zählt in Julianischen Jahrhunderten ab 1850.0). Le Verrier bemerkte aber als erstes, dass seine −47,6″/Jh. dem beobachteten Wert von etwa 45,8″/Jh. leicht widersprachen.
Die Ekliptikschiefe von Newcomb (1895) bis zur Raumfahrt
Gegen Ende des 19. Jahrhunderts war der allgemein akzeptierte Wert jener von John Nelson Stockwell (1873), nämlich ± 1,311379° bzw. −48,968″ / Jh. Später wurde für dieses Problem ein Preis ausgeschrieben, für den Paul Harzer 1895 alle säkularen Bahnstörungen der 8 großen Planeten berechnete. Um hierfür die (vor Albert Einstein noch unerklärliche) Periheldrehung des Merkur zu berücksichtigen, nahm er eine spezielle Massenverteilung in der Sonne an, und erhielt 47,499″ (bzw. ohne die Korrektur 0,14″ weniger). Im selben Jahr entwickelte Simon Newcomb seine Theorie der Fundamentalastronomie und benutzte Beobachtungen vieler berühmter Sternwarten. Seine bis etwa 1970 verwendeten Werte sind:
 (T ab 1900.0).
(T ab 1900.0).
Eine Neuberechnung von Eric Doolittle 1905 wich davon nur um 0,07″ ab, was nicht viel über der damaligen Messgenauigkeit von ε lag. Das in T quadratische Polynom ist allerdings nur als Approximation zu verstehen, da sich die Ekliptikschiefe periodisch ändert. Um 1960 nahm man dafür 41.050 Jahre an.
Aktueller Stand der Theorie
Heute kennen wir durch die interplanetaren Raumsonden die Planetenmassen etwa 100-mal genauer. 1970 berechnete J. Lieske den Trend zu:
Aus allen geeigneten Beobachtungen bis zurück zur Zeit Leonhard Eulers (s. oben) erhält man für 1817 ε = 23° 27′ 47,1″ – was von den Werten der damaligen Astronomen nur um 0,5″ abweicht.
1984 ging man auf die Bezugs-Epoche J2000.0 über:
Der Unterschied zum System 1970 liegt mit 0,008″ unter der damaligen Standardabweichung.
Axel D. Wittmann publizierte 1984 eine Ausgleichsrechnung, die auf circa 60 von 230 historischen Solstitialbeobachtungen fußt und von ihm neu reduziert wurden. Er erhielt neben einem Polynom 3. Grades auch eine Formel mit einem Sinusglied[2]:

(T bezüglich J2000.0)
Das Astronomical Almanac führte 1984 folgende Formel ein, die auch von der IAU angenommen wurde[3]:

(T bezüglich J2000.0)
Jacques Laskar gibt 1986 eine Formel an, die im Zeitraum J2000.0 ± 10.000 Julianische Jahre (also ± 100T) Gültigkeit hat.[4] Die größte Abweichung zwischen den Jahren +1000 und +3000 ist etwa 0,01″ und an den Gültigkeitsgrenzen einige wenige Bogensekunden:

mit U = T / 100 (T bezüglich J2000.0)
Messung der Schiefe der Ekliptik
Die Ekliptikschiefe wird am besten durch präzise Mittagshöhen am Meridiankreis der Sonne bestimmt, die zu verschiedenen Jahreszeiten wiederholt gemessen werden. Aus dem Höhenwinkel erhält man durch Berücksichtigung von geographischer Breite, atmosphärischer Strahlenbrechung (Refraktion) und verschiedener Eichgrößen des Fernrohrs die Deklination δ und daraus die ekliptikalen Längen λ der Sonne.
Durch den zeitlichen Verlauf der Deklination δ zwischen den Grenzen +ε und −ε erhält man ε zum mittleren Zeitpunkt der Beobachtungen. Dabei wird δ als Sinus-ähnliche Funktion von ε und der Länge λ angesetzt; letztere hängt mit den Kepler-Gesetzen zusammen. Die Bahnstörungen über diese Zusammenhänge sind allerdings nicht vernachlässigbar.
Unsere heutigen Analyse- und EDV-Methoden erlauben solche Berechnungen – unter anderem mittels Simulation der Planetenbahnen durch numerische Integration – wesentlich schneller und genauer als zu Zeiten von Newcomb. Dennoch hat man erst um 1980 und um 2000 die fundamentalen IAU-Konstanten den neuesten Resultaten anpassen müssen.
Tabelle der Ekliptikschiefe
−3000 bis +3000 Jahr Schiefe Jahr Schiefe −3000 24° 01,6′ 0 23° 41,7′ −2500 23° 58,7′ +500 23° 38,0′ −2000 23° 55,6′ +1000 23° 34,1′ −1500 23° 52,4′ +1500 23° 30,3′ −1000 23° 49,0′ +2000 23° 26,4′ −500 23° 45,4′ +2500 23° 22,5′ 0 23° 41,7′ +3000 23° 18,6′ +1600 bis +2200 Jahr Schiefe +1600 23° 29,5′ +1700 23° 28,7′ +1800 23° 27,9′ +1900 23° 27,1′ +2000 23° 26,4′ +2100 23° 25,6′ +2200 23° 24,9′ Man sieht bereits aus diesen 6 von 40 Jahrtausenden, dass sich die Änderung per 500 Jahre von −2,9′ auf −3,9′ beschleunigt, weil die absinkende Sinuswelle noch bis ins 5. Jahrtausend steiler wird (Mittelwert ε = 23° 06′ um das Jahr 4300).
Siehe auch
Literatur
- Andreas Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung. BI-Wiss.-Verl., Mannheim 1994, ISBN 3-411-17051-4.
Einzelnachweise
- ↑ Andreas Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung. 1994, S. 160.
- ↑ Axel D. Wittmann: On the Variation of the Obliquity of the Ecliptic, in: Mitteilungen der Astronomischen Gesellschaft, Vol. 62, S.201
- ↑ Astronomical Almanac for the year 1984, Washington, D.C., 1983. p. S26
- ↑ J. Laskar, Astronomy and Astrophysics, 157 (1986), 68: New Formulas for the Precession, Valid Over 10000 years
Weblinks
Wikimedia Foundation.